字节跳动

2018字节跳动测试开发第一批

第一题

时间复杂度，空间复杂度要求：

时间限制：1秒
空间限制：32768K

问题描述：

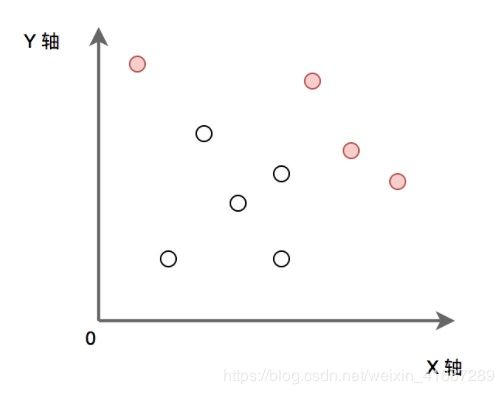
P为给定的二维平面整数点集。定义 P 中某点x，如果x满足 P 中任意点都不在 x 的右上方区域内
（横纵坐标都大于x），则称其为“最大的”。求出所有“最大的”点的集合。（所有点的横坐标和纵坐标都不重复
, 坐标轴范围在[0, 1e9) 内）

如下图：实心点为满足条件的点的集合。请实现代码找到集合 P 中的所有 ”最大“ 点的集合并输出。

输入描述：

第一行输入点集的个数 N， 接下来 N 行，每行两个数字代表点的 X 轴和 Y 轴。
对于 50%的数据,  1 <= N <= 10000;
对于 100%的数据, 1 <= N <= 500000;

输出描述：

输出“最大的” 点集合， 按照 X 轴从小到大的方式输出，每行两个数字分别代表点的 X 轴和 Y轴。

输入示例：

5
1 2
5 3
4 6
7 5
9 0

输出示例：

4 6
7 5
9 0

思路：

上来就是干。写了个O(n^2)的算法，只过了20%的case。。
O(n^2)的思路：
	对于每一个点，遍历整个列表，看看谁的x比它大而且y也比它大。如果有，这个点就不是目标值。

O(nlogn的思路)
后来老感觉抓住了点什么东西，又感觉没抓住。想了想，可以先按照x排下序(nlogn)，从x的最大值开始遍历，
这样的话对于每个x来讲，只需要判断之前出现过的最大的y是不是比自己的y要大就可以了。不大就是
最大值。 耗时O(n)
应该还有更好的办法，因为这个办法只过了80%的case。

解决方案1(O(n^2)):

nums = int(input())
s = set()
# 读入数据
for i in range(nums):
    a,b = input().split()
    k = int(a),int(b)
    s.add(k)
res = set()
for i in s:
    flag = True
    for j in s:
        if j[0]>i[0] and j[1]>i[1]:
            flag = False
            break
    if flag:
        res.add(i)
res = list(res)
res.sort(key=lambda x:x[0])

for i in res:
    print(i[0],i[1])

解决方案2：

nums = int(input())
l = []
for i in range(nums):
    x,y = input().split()
    k = int(x),int(y)
    l.append(k)

l.sort(key=lambda m:m[0])
res = []
max_y = None
for i in range(nums-1,-1,-1):
    if i == nums-1:
        res.append(l[i])
        max_y = l[i][1]
        continue
    if l[i][1] >= max_y:
        res.append(l[i])
        max_y = l[i][1]
    else:
        continue
res = res[::-1]
for i in res:
    print(i[0],i[1])

当然也可以对y进行排序：

n = int(input())
l = []
for i in range(n):
    a,b = input().split()
    a,b = int(a),int(b)
    l.append((a,b))
l.sort(key=lambda x:x[1])
current = []
current.append(l[-1])
max_x = l[-1][0]
for i in range(n-2,-1,-1):
    if l[i][0] > max_x:
        max_x = l[i][0]
        current.append(l[i])
for i in current:
    print(i[0],i[1])

第二题

空间、时间复杂度

时间限制：3秒
空间限制：131072K

问题描述：

给定一个数组序列, 需要求选出一个区间, 使得该区间是所有区间中经过如下计算的值最大的一个：

区间中的最小数 * 区间所有数的和最后程序输出经过计算后的最大值即可，不需要输出具体的区间。如给定序列  [6 2 1]则根据上述公式, 可得到所有可以选定各个区间的计算值:

 

[6] = 6 * 6 = 36;

[2] = 2 * 2 = 4;

[1] = 1 * 1 = 1;

[6,2] = 2 * 8 = 16;

[2,1] = 1 * 3 = 3;

[6, 2, 1] = 1 * 9 = 9;

 

从上述计算可见选定区间 [6] ，计算值为 36， 则程序输出为 36。

区间内的所有数字都在[0, 100]的范围内;

输入描述：

第一行输入数组序列长度n，第二行输入数组序列。
对于 50%的数据,  1 <= n <= 10000;
对于 100%的数据, 1 <= n <= 500000;

输出描述：

输出数组经过计算后的最大值。

输入样例：

3
6 2 1

输出样例：

36

思路：

跟leetcode的11题 盛水最多的容器差不多。都是最短的，最小的是限制条件。
这题的话，对于某个区间的最小值来讲，区间越大，求出来的target才越大。
所以，可以通过最小值划分区间。 找到某区间的最小值，以此为分界线，将原区间分成两个区间。
递归的算下去就可以了。
但是递归的话会导致占用内存太多。
所以还可以用非递归的办法。

烦的一比这个题，用递归写能过60%的测试样例，用非递归能过70%的测试样例。

解决方案(递归)：

nums = int(input())
k = list(input().split())
for i,v in enumerate(k):
    k[i] = eval(v)
maxs = max(k)**2
def find_max(l):
    if not len(l):
        return
    global maxs
    target = min(l)*sum(l)
    if target > maxs:
        maxs = target
    index = l.index(min(l))
    find_max(l[:index])
    find_max(l[index+1:])
find_max(k)
print(maxs)

解决方案2 非递归：

nums = int(input())
k = list(input().split())
for i,v in enumerate(k):
    k[i] = eval(v)
maxs = 0

res = []
res.append(k)
while res:
    target = None
    temp = []
    for i in res:
        target = min(i)*sum(i)
        if target > maxs:
            maxs = target
        index = i.index(min(i))
        left = i[:index]
        right = i[index+1:]
        if left:
            temp.append(left)
        if right:
            temp.append(right)
    res = temp
print(maxs)