Leetcode85 最大矩形 C++,Java,Python

Leetcode85 最大矩形

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximal-rectangle/

博主Github：https://github.com/GDUT-Rp/LeetCode

题目：

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1:

输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出: 6

解题思路：

方法一：暴力

直观想法

最原始地，我们可以列举每个可能的矩形。这可以通过遍历所有的(x1, y1) (x2, y2) 坐标，并以它们为对角顶点来完成。该方法过慢，不足以通过所有测试用例。

复杂性分析

• 时间复杂度： $O(N^3{M}^3)$。其中 N为行数， M 为列数。
  • 遍历全部坐标的复杂度是$O(N^2{M}^2)$, 遍历以该两点为对角顶点的矩形又会耗费 $O(NM)$。故总体复杂度为$O(NM)\ast O(N^2{M}^2)=O(N^3{M}^3)$
• 空间复杂度 $O(1)$ 的额外空间。

方法二：动态规划 - 使用柱形图的优化暴力方法

算法

我们可以以常数时间计算出在给定的坐标结束的矩形的最大宽度。我们可以通过记录每一行中每一个方块连续的“1”的数量来实现这一点。每遍历完一行，就更新该点的最大可能宽度。通过以下代码即可实现。 row[i] = row[i - 1] + 1 if row[i] == '1'.

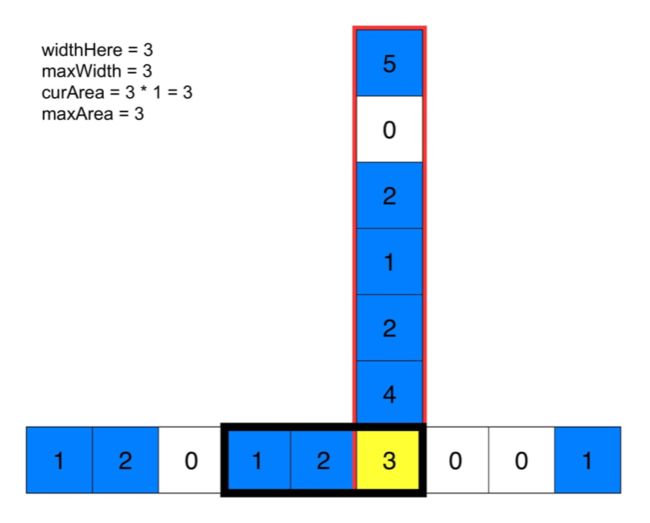
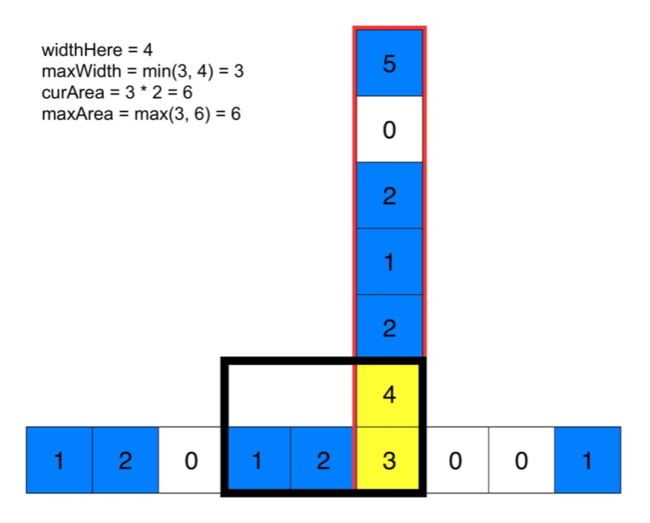
一旦我们知道了每个点对应的最大宽度，我们就可以在线性时间内计算出以该点为右下角的最大矩形。当我们遍历列时，可知从初始点到当前点矩形的最大宽度，就是我们遇到的每个最大宽度的最小值。 我们定义：

$$maxWidth=min(maxWidth,widthHere)$$

$$curArea=maxWidth\ast (curre\ast \ast \ast ow-originalRow+1)$$

$$maxArea=max(maxArea,curArea)$$

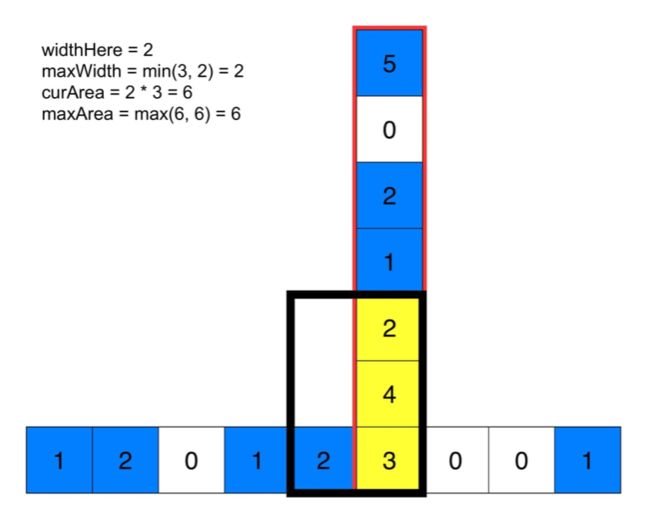
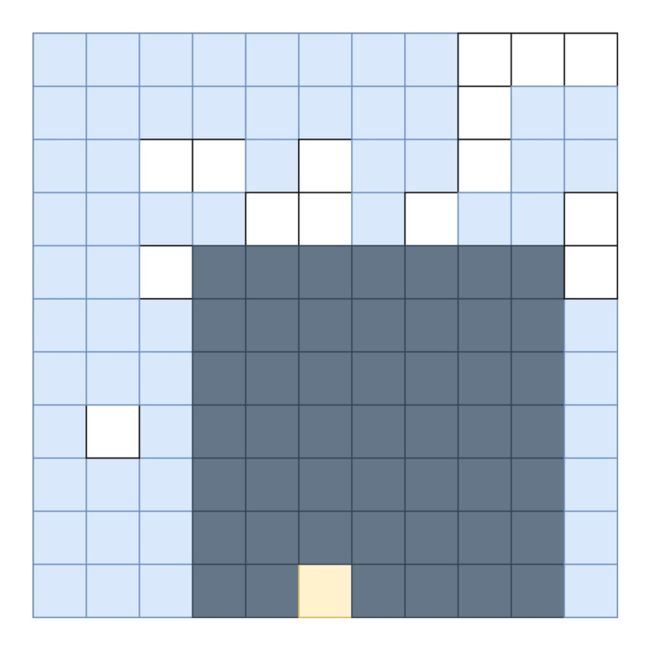
下面的动画有助于理解。给定每个点的最大宽度，可计算出底端黄色方块的最大矩形面积。

对每个点重复这一过程，就可以得到全局最大。

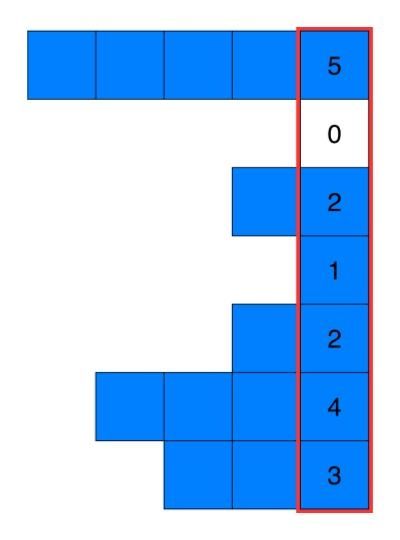
注意，我们预计算最大宽度的方法事实上将输入转化成了一系列的柱状图，每一栏是一个新的柱状图。我们在针对每个柱状图计算最大面积。

C++:

class Solution {
public:
    int maximalRectangle(vector<vector<char>> &matrix) {
        if (matrix.size() == 0) {
            return 0;
        }
        int maxarea = 0;
        int dp[matrix.size()][matrix[0].size()];
        memset(dp, 0, sizeof(dp));  //  初始化为0

        for (int i = 0; i < matrix.size(); ++i) {
            for (int j = 0; j < matrix[0].size(); ++j) {
                if (matrix[i][j] == '1') {
                    dp[i][j] = j == 0 ? 1 : dp[i][j - 1] + 1;           //  dp,计算宽度
                    int width = dp[i][j];

                    for (int k = i; k >= 0; k--) {
                        width = min(width, dp[k][j]);                   //  向上每次取该行向下最短宽
                        maxarea = max(maxarea, width * (i - k + 1));    //  最短宽 * 高度
                    }
                }
            }
        }
        return maxarea;
    }
};

Java:

class Solution {
    public int maximalRectangle(char[][] matrix) {

        if (matrix.length == 0) return 0;
        int maxarea = 0;
        int[][] dp = new int[matrix.length][matrix[0].length];

        for(int i = 0; i < matrix.length; i++){
            for(int j = 0; j < matrix[0].length; j++){
                if (matrix[i][j] == '1'){

                    // compute the maximum width and update dp with it
                    dp[i][j] = j == 0? 1 : dp[i][j-1] + 1;

                    int width = dp[i][j];

                    // compute the maximum area rectangle with a lower right corner at [i, j]
                    for(int k = i; k >= 0; k--){
                        width = Math.min(width, dp[k][j]);
                        maxarea = Math.max(maxarea, width * (i - k + 1));
                    }
                }
            }
        } return maxarea;
    }
}

Python:

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        maxarea = 0

        dp = [[0] * len(matrix[0]) for _ in range(len(matrix))]
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if matrix[i][j] == '0': continue

                # compute the maximum width and update dp with it
                width = dp[i][j] = dp[i][j-1] + 1 if j else 1

                # compute the maximum area rectangle with a lower right corner at [i, j]
                for k in range(i, -1, -1):
                    width = min(width, dp[k][j])
                    maxarea = max(maxarea, width * (i-k+1))
        return maxarea

复杂性分析

• 时间复杂度： $O(N^{2}M)$。由于需要遍历同一列中的值，计算每个点对应最大面积需要$O(N)$。对全部$N\ast M$个点都要计算，因此总共$O(N)\ast O(NM)=O(N^{2}M)$。
• 空间复杂度 $O(NM)$ 的额外空间。 我们分配了一个等大的数组，用于存储每个点的最大宽度。

方法三：动态规划 - 每个点的最大高度

算法

想象一个算法，对于每个点我们会通过以下步骤计算一个矩形：

不断向上方遍历，直到遇到“0”，以此找到矩形的最大高度。

向左右两边扩展，直到无法容纳矩形最大高度。

例如，找到黄色点对应的矩形：

给定一个最大矩形，其高为 h， 左边界 l，右边界 r，在矩形的底边，区间 [l, r] 内必然存在一点，其上连续1的个数（高度）<=h。若该点存在，则由于边界内的高度必能容纳 h，以上述方法定义的矩形会向上延伸到高度h，再左右扩展到边界 [l, r] ，于是该矩形就是最大矩形。

若不存在这样的点，则由于 [l, r]内所有的高度均大于 h，可以通过延伸高度来生成更大的矩形，因此该矩形不可能最大。

综上，对于每个点，只需要计算h，l，和 r - 矩形的高，左边界和右边界。

使用动态规划，我们可以在线性时间内用上一行每个点的 h，l，和 r 计算出下一行每个点的的h，l，和r。

算法

给定一行 matrix[i]，我们通过定义三个数组height，left，和 right来记录每个点的h，l，和 r。height[j] 对应matrix[i][j]的高，以此类推。

问题转化为如何更新每个数组。

Height:

这个比较容易。 h 的定义是从该点出发连续的1的个数。我们从方法二中已经学会了在一行中计算的方法:

row[j] = row[j - 1] + 1 if row[j] == '1'
只需要一点改动即可:

new_height[j] = old_height[j] + 1 if row[j] == '1' else 0
Left:

考虑哪些因素会导致矩形左边界的改变。由于当前行之上的全部0已经考虑在当前版本的left中，唯一能影响left就是在当前行遇到0。

因此我们可以定义:

new_left[j] = max(old_left[j], cur_left)
cur_left是我们遇到的最右边的0的序号加1。当我们将矩形向左 “扩展” ，我们知道，不能超过该点，否则会遇到0。

Right:

我们可以沿用 left 的思路，定义:

new_right[j] = min(old_right[j], cur_right)
cur_right 是我们遇到的最左边的0的序号。简便起见，我们不把 cur_right 减去1 (就像我们给cur_left加上1那样) ，这样我们就可以用height[j] * (right[j] - left[j]) 而非height[j] * (right[j] + 1 - left[j])来计算矩形面积。

这意味着， 严格地说 ，矩形的底边由半开半闭区间[l, r) 决定，而非闭区间 [l, r]，且 right比右边界大1。尽管不这样做算法也可以正确运行，但这样会让计算看起来更简洁。

注意，为了正确的记录 cur_right，我们需要从右向左迭代。因此，更新right时需要从右向左。

一旦left，right，和 height数组能够正确更新，我们就只需要计算每个矩形的面积。

由于我们知道矩形 j的边界和高，可以简单地用height[j] * (right[j] - left[j])来计算面积，若j的面积 大于max_area，则更新之。

.

C++:

int maximalRectangle_stack(vector<vector<char>> &matrix) {
    if (matrix.size() == 0) {
        return 0;
    }
    int m = matrix.size();
    int n = matrix[0].size();
    int left[n];
    int right[n];
    int height[n];

    memset(right, n, sizeof(right));
    memset(left, n, sizeof(left));
    memset(height, n, sizeof(height));

    int maxarea = 0;
    for (int i = 0; i < m; ++i) {
        int cur_left = 0, cur_right = n;
        // update height
        for (int j = 0; j < n; ++j) {
            if (matrix[i][j] == '1') {
                height[j]++;
            } else {
                height[j] = 0;
            }
        }
        // update left
        for (int j = 0; j < n; ++j) {
            if (matrix[i][j] == '1') {
                left[j] = max(left[j], cur_left);
            } else {
                left[j] = 0, cur_left = j + 1;
            }
        }
        //  update right
        for (int j = n - 1; j >= 0; --j) {
            if (matrix[i][j] == '1') {
                right[j] = min(right[j], cur_right);
            } else {
                right[j] = n;
                cur_right = j;
            }
        }
        //  update area
        for (int j = 0; j < n; ++j) {
            maxarea = max(maxarea, (right[j] - left[j]) * height[j]);
        }
    }
    return maxarea;
}

Java:

class Solution {

    public int maximalRectangle(char[][] matrix) {
        if(matrix.length == 0) return 0;
        int m = matrix.length;
        int n = matrix[0].length;

        int[] left = new int[n]; // initialize left as the leftmost boundary possible
        int[] right = new int[n];
        int[] height = new int[n];

        Arrays.fill(right, n); // initialize right as the rightmost boundary possible

        int maxarea = 0;
        for(int i = 0; i < m; i++) {
            int cur_left = 0, cur_right = n;
            // update height
            for(int j = 0; j < n; j++) {
                if(matrix[i][j] == '1') height[j]++;
                else height[j] = 0;
            }
            // update left
            for(int j=0; j<n; j++) {
                if(matrix[i][j]=='1') left[j]=Math.max(left[j],cur_left);
                else {left[j]=0; cur_left=j+1;}
            }
            // update right
            for(int j = n - 1; j >= 0; j--) {
                if(matrix[i][j] == '1') right[j] = Math.min(right[j], cur_right);
                else {right[j] = n; cur_right = j;}    
            }
            // update area
            for(int j = 0; j < n; j++) {
                maxarea = Math.max(maxarea, (right[j] - left[j]) * height[j]);
            }
        return maxarea;
    }
}

Python:

class Solution:

    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        if not matrix: return 0

        m = len(matrix)
        n = len(matrix[0])

        left = [0] * n # initialize left as the leftmost boundary possible
        right = [n] * n # initialize right as the rightmost boundary possible
        height = [0] * n

        maxarea = 0

        for i in range(m):

            cur_left, cur_right = 0, n
            # update height
            for j in range(n):
                if matrix[i][j] == '1': height[j] += 1
                else: height[j] = 0
            # update left
            for j in range(n):
                if matrix[i][j] == '1': left[j] = max(left[j], cur_left)
                else:
                    left[j] = 0
                    cur_left = j + 1
            # update right
            for j in range(n-1, -1, -1):
                if matrix[i][j] == '1': right[j] = min(right[j], cur_right)
                else:
                    right[j] = n
                    cur_right = j
            # update the area
            for j in range(n):
                maxarea = max(maxarea, height[j] * (right[j] - left[j]))

        return maxarea

复杂性分析

• 时间复杂度： $O(NM)$。每次对于N的迭代我们会对M迭代常数次。