「机器学习速成」分类,评估指标(TP、FP、TN、FN),ROC曲线和AUC
https://www.toutiao.com/a6706449645901464078/
2019-06-25 20:49:47
大家好,今天我们学习【机器学习速成】之 分类,评估指标(TP、FP、TN、FN),ROC曲线和AUC。
本节介绍了如何使用逻辑回归来执行分类任务, 并探讨了如何评估分类模型的有效性。
我们 马上学三点 ,
- 逻辑回归用作分类:指定阈值
- 评估指标:准确率、精确率和召回率
- ROC曲线和曲线下面积(AUC)
大家可以点击下面的“ 了解更多 ”, 或搜索“ 马上学123 ”, 在线观看PPT讲义。
分类与回归: 指定阈值
我们在之前“逻辑回归”一节介绍了关于回归的内容, 逻辑回归是一种极其高效的概率计算机制, 会生成一个介于0到1之间的概率值:
- 您可以“原样”使用返回的概率,
- 也可以将返回的概率转换成二元值。
现在,我们可以将逻辑回归用作分类的基础, 具体方法是利用概率输出并为其应用固定阈值。
例如,如果邮件为垃圾邮件的概率超过0.8, 我们可能就会将其标记为垃圾邮件, 0.8就是分类阈值。
阈值取决于具体问题, 我们要根据具体问题对其进行调整。 在选择阈值时, 需要评估您将因犯错而承担多大的后果。 例如, 将非垃圾邮件误标记为垃圾邮件会非常糟糕,要少标。 但是雷达检测导弹信号,就必须宁可多虚警也不能漏掉。
评估指标:准确率
选定分类阈值之后, 如何评估相应模型的性能呢?
我们需要一些新指标, 评估分类效果的一种传统方式是使用准确率。 我们所说的准确率指的是正确结果数除以总数。 根本上讲,就是正确结果所占的百分比。 值得注意的是,虽然准确率是一种非常直观 且广泛使用的指标,但它也有一些重大缺陷。
准确率可能具有误导性
特别是, 如果问题中存在类别不平衡的情况, 那么准确率指标的效果就会大打折扣。
例如, 在100个肿瘤样本中,91个为良性,9个为恶性。 在91个良性肿瘤中, 某个模型将90个正确识别为良性。 准确率很好。 不过,在9个恶性肿瘤中, 该模型仅将1个正确识别为恶性。 这是多么可怕的结果! 9个恶性肿瘤中有8个未被诊断出来!
虽然91%的准确率可能乍一看还不错, 但如果另一个肿瘤分类器模型总是预测良性, 那么这个模型使用我们的样本进行预测 也会实现相同的准确率(100个中有91个预测正确)。 换言之,我们的模型 与那些没有预测能力来区分恶性肿瘤和良性肿瘤的模型差不多。 显然,准确率并不适用于这种情况。
真正例TP、假正例FP、假负例FN和真负例TN:
为了处理类别不平衡问题, 我们需要采用更精细的方法来观察, 模型如何预测正类别、负类别或不同类别。
我们可以考虑将这些不同类型的成功和失败结果 放入2x2混淆矩阵中, 其中包括真正例TP、假正例FP、假负例FN和真负例TN:
真正例TP、假正例FP、假负例FN和真负例TN
- 真正例是指模型将正类别样本正确地预测为正类别;
- 真负例是指模型将负类别样本正确地预测为负类别;
- 假正例是指模型将负类别样本错误地预测为正类别;
- 假负例是指模型将正类别样本错误地预测为负类别。
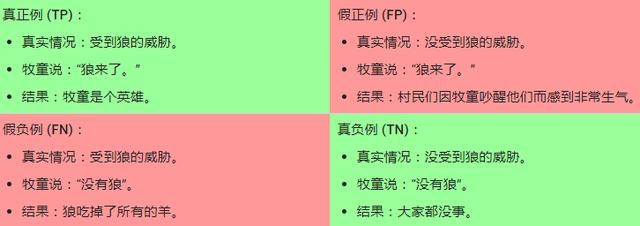
真正例和假正例,举例:狼来了
为了方便理解, 我们想想“狼来了”这则故事,这个小男孩是一个牧童:
真正例TP、假正例FP、假负例FN和真负例TN
- 如果狼来了,小男孩正确地指出来, 这就是真正例。 他看到了狼并说“狼来了”。 真正例对应的结果是小镇得救,这很好。
- 假正例则是小男孩说“狼来了”, 但其实并没有狼。 这就是假正例,会令所有人非常恼火。
- 假负例的后果可能更严重。 假负例对应的情形是, 狼来了而小男孩睡着了或没看到, 狼进入镇子并吃掉了所有的鸡。 这可真的太惨了。
- 真负例对应的情形是小男孩没喊“狼来了”, 狼也确实没出现,一切安好。
评估指标:精确率和召回率
我们可以将这些预期情况组合成几个不同的指标:
- 其中一个就是精确率, 也就是, 在小男孩说“狼来了”的情况中, 有多少次是对的? 他说“狼来了”的精确率如何?
- 另一方面,召回率指标则是指: 在所有试图进入村庄的狼中,我们发现了多少头?
值得注意的是, 这些指标往往处于此消彼长的状态:
- 如果您希望在召回率方面做得更好, 那么即使只是听到灌木丛中传出的一点点声响, 也要早些指出“狼来了”。 我们认为这种做法会降低分类阈值。
- 如果我们希望非常精确, 那么正确的做法是只在我们完全确定时才说“狼来了”, 我们认为这样会提高分类阈值。
这两个指标往往处于此消彼长的状态, 而在这两个方面都做好非常重要。 这也意味着, 每当有人告诉您精确率值是多少时, 您还需要问召回率值是多少, 然后才能评价模型的优劣。
ROC 曲线:真正例率 (TPR) 、假正例率 (FPR)
我们选择特定的分类阈值后, 精确率和召回率值便都可以确定。
但我们可能无法事先得知最合适的分类阈值, 而我们仍然想知道我们的模型质量如何。
合理的做法是尝试使用许多 不同的分类阈值来评估我们的模型。 事实上,我们有一个指标可衡量模型 在所有可能的分类阈值下的效果。 该指标称为ROC曲线,即接收者操作特征曲线。
ROC曲线具体概念是: 我们对每个可能的分类阈值进行评估, 并观察相应阈值下的真正例率和假正例率。
ROC 曲线:真正例率 (TPR) 、假正例率 (FPR)
- 横轴FP假正例率(误报率), 模型预测错误的狼来了占真实情况狼没有来的比例;
- 纵轴TP真正例率(召回率), 模型预测正确的狼来了占真实情况狼来了的比例;
ROC 曲线
ROC 曲线
ROC曲线用于绘制采用不同分类阈值时的TPR与FPR。 降低分类阈值会导致将更多样本归为正类别, 从而增加假正例和真正例的个数。
评估指标:曲线下面积
为了计算 ROC 曲线上的点, 我们可以使用不同的分类阈值多次评估逻辑回归模型, 但这样做效率非常低。 幸运的是, 有一种基于排序的高效算法可以为我们提供此类信息, 这种算法称为曲线下面积, 也称为AUC(Area Under Curve)。
曲线下面积
借助曲线下面积,我们可以有效解读概率。
举例解释一下: 如果我拿一个随机正分类样本, 然后再拿起一个随机负分类样本, 则模型正确地将较高分数分配给正分类样本 而非负分类样本的概率是多少? 结果表明, 这个概率正好等于ROC曲线下面积代表的概率值。 因此,如果我看到ROC曲线下面积的值是0.9, 那么这就是得出正确的配对比较结果的概率。
曲线下面积(AUC)对所有可能的分类阈值的效果 进行综合衡量。
AUC值是一个概率值, 当你随机挑选一个正样本以及负样本, 当前的分类算法根据计算得到的Score值 将这个正样本排在负样本前面的概率就是AUC值, AUC值越大, 当前分类算法越有可能将正样本排在负样本前面, 从而能够更好地分类。
所以,AUC曲线的物理意义为: 任取一对(正、负)样本, 正样本的置信度大于负样本的置信度的概率。
曲线下面积的取值范围为0-1:
- 预测结果 100% 错误的模型的曲线下面积为 0.0;
- 预测结果 100% 正确的模型的曲线下面积为 1.0;
- ROC曲线越靠近左上角,模型的准确性就越高;
- 如果两条ROC曲线发生了交叉, 可以比较ROC曲线下的面积,即AUC选模型;
总结:
- 逻辑回归用作分类,指定阈值,阈值取决于具体问题
- 评估指标:准确率(accuracy)、精确率(precision)、召回率(recall)
- ROC曲线对每个可能的分类阈值进行评估, 并观察相应阈值下的真正例率和假正例率。
- AUC曲线的物理意义为:任取一对(正、负)样本,正样本的置信度大于负样本的置信度的概率
这里讲了三点,关键词有哪几个?
提问,论文中一般使用那些评估指标?