ARIMA
1. 简介&基础知识
ARIMA是典型的时间序列模型，其由三部分组成：AR模型（自回归模型）和MA模型（滑动平均模型），以及差分的阶数I，因此ARMA称为自回归滑动平均模型。
差分运算常用公式如下：
- 平稳时间序列：
平稳时间序列满足下述的弱平稳公式。
平稳时间序列检测方法：ADF单位根检验。 - 差分方程的稳定性：
如果特征方程的所有根均落在单位圆内，那么差分方程系统是稳定的。
- 弱平稳&白噪声
2. AR模型
AR模型认为当前时刻和前面的时刻有关，公式如下：
y t = α 0 + α 1 y t − 1 + α 2 y t − 2 + . . . + α p y t − p + ϵ t y_t=\alpha_0 + \alpha_1 y_{t-1} +\alpha_2 y_{t-2}+...+\alpha_p y_{t-p} +\epsilon_t yt=α0+α1yt−1+α2yt−2+...+αpyt−p+ϵt
以上称为p阶自回归模型，简记为 A R ( p ) AR(p) AR(p)模型。
其中 ϵ t \epsilon_t ϵt要满足白噪声过程（弱平稳的一种）（期望为0，方差为 σ 2 \sigma^2 σ2）
此外，还要求差分方程是平稳的，检验方法为上述差分方差稳定性特征根检验。对于AR模型，要满足平稳性条件， ∣ α ∣ < 1 |\alpha|<1 ∣α∣<1
3. MA
3.ARMA
4. ARIMA建模流程及实例
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# 第一步：读取数据
df = pd.read_excel(r'D:\002study\finance\szzz.xlsx', encoding='utf-8', index_col=0, parse_dates=True)
df.head()
# 第二步：选择数据y，本任务选择收盘价作为y
data = df['收盘']
# 第三步：画图，观察数据
plt.figure(figsize = (10, 6))
plt.plot(df.index, data)
plt.show() # 从肉眼看不符合平稳时间序列
# 第四步：做一阶差分，观察数据
data_diff = data.diff()
data_diff = data_diff.dropna()
plt.plot(data_diff)
plt.show() # 肉眼看，大致是平稳时间序列
# 第五步：单位根检验，确定数据为平稳时间序列
from statsmodels.tsa.stattools import adfuller
adfuller(data_diff)
# -12.574267463093953,:ADF检验的结果
# 1.9731589957016685e-23：P值
# 33：滞后数量
# 5650：用于ADF回归和临界值计算的数量
# 字典：1% 5% 10% 临界值
# 从结果可以看出拒绝原假设（原假设为是平稳时间序列），故数据为平稳时间序列
(-12.574267463093953,
1.9731589957016685e-23,
33,
5650,
{'1%': -3.431507924506506,
'10%': -2.567042371180202,
'5%': -2.8620516903778443},
57221.03020322479)
# 第六步：Q检验-检验数据是否具有相关性
# 只有在序列有相关性，即t时刻的y与t-1时刻的y有关系时arma模型才有意义
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(data_diff, lags = 20) # 第一个数：统计值； 第二个数：p值
# 从结果可以看出，p值较小，拒绝原假设（没有相关性），故数据有序列相关性
(array([ 1.83314066, 3.82708483, 20.80922442, 31.68903555,
31.77117863, 37.01813495, 38.72831312, 46.0225279 ,
49.90083374, 51.88772656, 61.00733979, 72.7565523 ,
80.8251778 , 82.4664476 , 108.43977737, 108.59968661,
110.13831807, 118.29026563, 121.2904632 , 129.2911755 ]),
array([1.75757036e-01, 1.47556752e-01, 1.15329827e-04, 2.21448092e-06,
6.59439411e-06, 1.74661315e-06, 2.20208389e-06, 2.35366822e-07,
1.12448899e-07, 1.19704270e-07, 6.02304256e-09, 9.73426581e-11,
7.71532769e-12, 9.84274271e-12, 3.21200221e-16, 8.27333130e-16,
1.13657497e-15, 8.81599095e-17, 6.36139096e-17, 5.29373100e-18]))
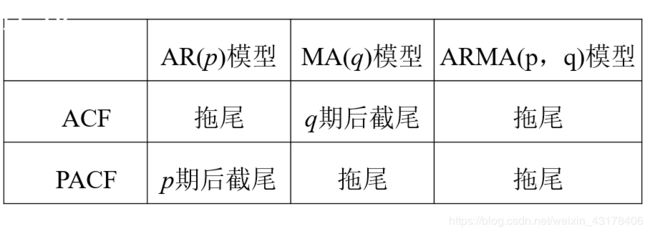
# 第七步：确定AR和MA的阶数-初步判断：画acf、pacf图（该种方式有时判断不出来）
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
pacf = plot_pacf(data_diff, lags=20)
plt.title('PACF')
pacf.show()
acf = plot_acf(data_diff, lags=20)
plt.title('ACF')
acf.show()
# 从图中大致可以看出，p=1；q=1
ACF和PACF的判断标准如下：
# 第八步：使用AIC、BIC最小准则确定p、q；当p、q阶数较小时，可用这种暴力解法
import statsmodels.tsa.stattools as st
model = st.arma_order_select_ic(data_diff, max_ar=5, max_ma=5, ic=['aic', 'bic', 'hqic'])
model.bic_min_order #返回一个元组，分别为p值和q值
(2,2)
# 第九步：拟合ARIMA或者ARMA模型
# 当使用data_diff的数据时，拟合ARMA模型：
# from statsmodels.tsa.arima_model import ARMA
# model_arma = ARMA(data_diff, order = model.bic_min_order)
# result_arma = model_arma.fit(disp = -1, method = 'css')
# 当使用data原始数据时，拟合ARIMA模型
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(data, order=(1,1,1))
result = model.fit()
# 第十步：检验模型效果：残差检验
# 如果残差是白噪声序列，说明时间序列中有用的信息已经被提取完毕了，剩下的全是随机扰动，是无法预测和使用的。
# 残差序列如果通过了白噪声检验，则建模就可以终止了，因为没有信息可以继续提取。
# 如果残差如果未通过白噪声检验，说明残差中还有有用的信息，需要修改模型或者进一步提取。
resid = result.resid
from statsmodels.graphics.api import qqplot
qqplot(resid, line='q', fit=True)
plt.show()
# qq图中：如果是正态分布则为一条直线，即红线。结果大致符合白噪声
# 白噪声检验除了qq图还可以使用DW检验法（DW：检验残差序列是否具有自相关性，只适用一一阶自相关；多阶自相关可用LM检验）
import statsmodels.api as sm
print(sm.stats.durbin_watson(resid.values))
# 从上边两步可以看出，残差序列是正态分布，且相互独立。因此可以认为是高斯白噪声，通过白噪声检验，建模可以终止。
-
残差图：残差他是以残差为纵坐标，以其他量为横坐标的散点图。
- 以因变量Y的拟合值为横坐标的散点图：大致分布在一个水平的带状区域内。
- 以自变量观测值为横坐标的散点图
- 以观测时间或预测值序号为横坐标的散点图 -
QQ图：QQ-plot(Q代表分位数Quantile)是一种通过画出分位数来比较两个概率分布的图形方法。首先选定区间长度，点(x,y)对应于第一个分布(x轴)的分位数和第二个分布(y轴)相同的分位数。因此画出的是一条含参数的曲线，参数为区间个数。如果被比较的两个分布比较相似，则其QQ图近似地位于y=x上。如果两个分布线性相关，则QQ图上的点近似地落在一条直线上，但并不一定是y=x这条线。QQ图同样可以用来估计一个分布的位置参数。残差检验中：横坐标为正态分布的分位数，纵坐标为残差的分位数
-
DW检验结果判断：该统计量的取值在0-4之间，仅适用于一阶自相关检验。根据样本数量n和解释变量数目k得到临界值 L D L_D LD和 U D U_D UD
(1)如果 0 < D W < L D 0<DW< L_D 0<DW<LD ，则拒绝零假设，扰动项存在一阶正自相关。DW 越接近于0，正自相关性越强。
(2)如果 L D < D W < U D L_D <DW< U_D LD<DW<UD ，则无法判断是否有自相关。
(3)如果 U D < D W < 4 − U D U_D <DW<4- U_D UD<DW<4−UD ，则接受零假设，扰动项不存在一阶正自相关。DW 越接近2，判断无自相关性把握越大。
(4)如果 4 − U D < D W < 4 − L D 4- U_D <DW<4- L_D 4−UD<DW<4−LD ，则无法判断是否有自相关。
(5) 如果 4 − L D < D W < 4 4- L_D <DW<4 4−LD<DW<4，则拒绝零假设，扰动项存在一阶负自相关。DW 越接近于4，负自相关性越强。
通过以上可知，模型在2左右时不存在自相关性 -
LM检验：LM服从卡方分布，值太大拒绝原假设（原假设为具有相关性）
# 第十一步：预测
pred = result.predict(start=1, end =len(data) + 10 ) # 从训练集第0个开始预测(start=1表示从第0个开始)，预测完整个训练集后，还需要向后预测10个
print(len(pred))
print(pred[-10:]) # 有负数，表明是一阶差分之后的
# 此时可以画出预测的曲线和data_diff进行比较
5695
5686 1.372057
5687 -0.485253
5688 0.992668
5689 -0.183361
5690 0.752443
5691 0.007793
5692 0.600335
5693 0.128831
5694 0.504022
5695 0.205470
dtype: float64
# 第十二步：将预测的平稳值还原为非平稳序列
result_fina = np.array(pred[0:-10]) + (np.array(data.shift(1)))
result_fina
# 如果还取了对数，进行如下操作
# result_log_rev = np.exp(result_fina)
# result_log_rev.dropna(inplace=True)