算法导论——分治法、归并排序——伪代码和Java实现

第二章第三节：分治法

    我们首先先介绍分治法。分治法的思想：将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后在合并这些子问题的解来解决原问题的解。

    还是拿扑克牌举例子，假设桌上有两堆牌面朝上的牌(牌面朝上：有值)，每堆都已排序，最小的牌在顶上。我们希望把这两堆牌合并成单一的排好序的输出堆，牌面朝下地放在桌上。应该怎么做呢？
    我们的做法是：在牌面朝上的两堆牌的顶上两张牌中选取较小的一张，将该牌从其堆中移开(该堆的顶上将显示一张新牌)并牌面朝下地将该牌放置到输出堆。重复这个步骤直到两堆牌都没有牌。
    下面我们来实现上面所提的思想
    为了避免在某个基本步骤必须检查是否有堆为空。在每个堆的底部放置一张哨兵牌，它包含一个特殊的值(很大的值，使它不可能是较小的牌，除非两个堆都已显露出其哨兵牌。一旦发生这种情况，说明非哨兵牌都已被放置到输出堆)，用于简化代码。

伪代码：

MERGE(A,p,q,r)
n1 = q - p + 1
n2 = r - q
//L[1..n1+1] and R[1..n2+1]是新的数组
for i = 1 to n1
	L[i] = A[p + i -1]
for j = 1 to n2
	R[j] = A[q + j]
L[n1 + 1] = ∞
R[n2 + 1] = ∞
i = 1
j = 1
for k = p to r
	if L[i] <= R[j]
		A[k] = L[i]
		i = i + 1
	else 
		A[k] = R[j]
		j = j + 1

Java实现：

public void Merge(int[] A,int p,int q,int r){
        int n1 = q - p + 1;
        int n2 = r - q;

        //L[1..n1+1] and R[1..n2+1]是新的数组
        int[] L = new int[n1 + 1];
        int[] R = new int[n2 + 1];

        for (int i = 0;i < n1;i++){
            L[i] = A[p + i];
        }
        for (int j = 0;j < n2;j++){
            R[j] = A[q + j + 1];
        }

        L[n1] = Integer.MAX_VALUE;
        R[n2] = Integer.MAX_VALUE;

        int i = 0,j = 0;
        for (int k = p;k <= r;k++){
            if (L[i] <= R[j]){
                A[k] = L[i];
                i = i + 1;
            }else{
                A[k] = R[j];
                j = j + 1;
            }
        }
    }

    下面我们来看一下分治法的步骤
    对数组A[2,4,7,1,3,6]调用Merge(A,0,2,5)

初始状态↓

    初始完L和R数组之后，现在进入for循环阶段。让L中i所指的值和R数组中j所指的值进行比较，把较小的值放入数组A中k所指的位置。并且让较小的值的索引i或j前进一格(+1)。因为L和R数组已经从小到大排好序了，所以找出来的最小值一定是当前L和R数组的最小值，放入了数组A中也是排好序的，所以让k前进一步，k=k+1,然后执行下一次循环。
第一此循环：i和j初始为0，k=p=0，让L[0]与R[0]进行比较 L[0]>R[0]所以R[0]是较小值，把A[0]替换为R[0]。让j=j+1，i保持不变。k=k+1=1，开启下一次循环。本次循环结果如下图所示：
    A中的灰色位置包含将被覆盖的值，L和R中的灰色位置包含有待于被复制回A的值，A中的黄色位置包含它们的最终值，L和R中的黄色位置包含已被复制回A的值。

    第二次循环：此时i=0，j=1，k=1，让L[i]和R[j]进行比较，L[0]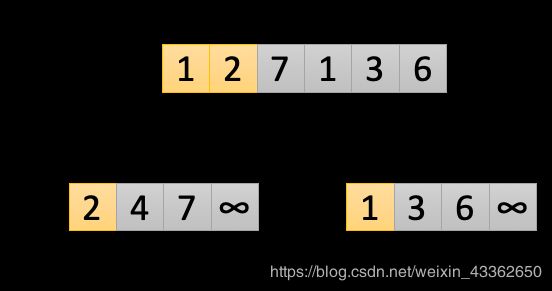
    第三次循环：此时i=1，j=1，k=2，让L[i]和R[j]进行比较，L[1]>R[1]，所以R[1]是较小值，把A[2]即A[2]替换为R[1]。让j=j+1，i保存不变。k=k+1=3，开启下一次循环。本次循环结果如下图所示：

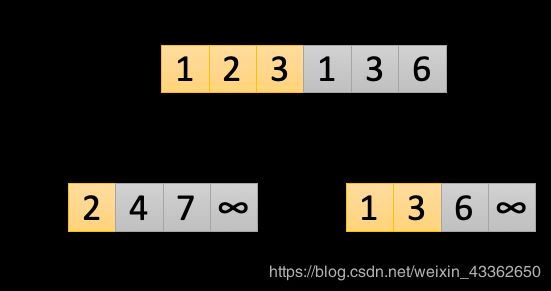
    第四次循环：此时i=1，j=2，k=3，让L[i]和R[j]进行比较，L[1]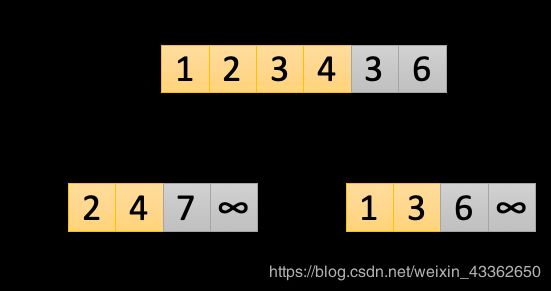
    第五次循环：此时i=2，j=2，k=4，让L[i]和R[j]进行比较，L[2]>R[2]，所以R[2]是较小值，把A[k]即A[4]替换为R[2]。让j=j+1，j保存不变。k=k+1=4，开启下一次循环。本次循环结果如下图所示：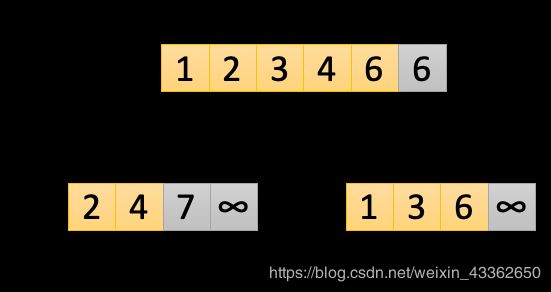
    注意：此时j已经到达了R数组的最后一个数∞，L数组中的每个数都比∞小，即不等式L[i]>R[j]恒成立。所以不管L剩下多少个数，都会按照顺序放置A中，直到i也达到了最后一个数∞，此时k>r，循环已经全部结束。
    第六次循环：此时i=2，j=3，k=5，让L[i]和R[j]进行比较，L[2]
    第七次循环，此时i=2，j=3，k=6，我们的r=5，判断条件k<=r为false，循环结束。

分治法的应用——归并排序

    上面讲到了分治法，分治法有个很大的限制就是L和R是排好序的才可以。但是许多数组都是很乱的顺序。那么怎么解决这个问题呢？试想一下如果L和R数组的大小为1，那么L和R数组肯定是排好序的。对的！我们可以把一个大的数组递归拆分成小的子数组，子数组在递归拆分成更小的子数组。直到递归到的L和R数组的大小为1时，调用MERGE分治法。随着算法自底向上地推进：合并只含1项的序列对形成长度为2的排好序的序列，合并长度为2的序列对形成长度为4的排好序的序列，依次下去，直到长度为n/2的两个序列被合并最终形成长度为n的排好序的序列，数组最终会排序完成。

如下图所示

    我们可以把上面提到的MERGE作为归并排序算法中的一个子程序来用。
    下面的过程MERGE-SORT(A,p,r)排序子数组A[p…r]中的元素。若p>=r,则该子数组最多有一个元素，所以已经排好序。否则，分解步骤简单地计算一个下标q，将A[p…r]分成两个子数组A[p…q]和A[q+1…r]，前者包含⌈n/2⌉个元素，后者包含⌊n/2⌋个元素。
伪代码：

MERGE-SORT(A,p,r)
if p < r
	q = ⌊(p+r)/2⌋
	MERGE-SORT(A,p,q)
	MERGE-SORT(A,q+1,r)
	MERGE(A,p,q,r)

java实现：

public void MergeSort(int[] A,int p,int r) {
        if (p < r){
            int q =(int)Math.floor((p+r)/2);	
            MergeSort(A,p,q);			//将左半边排序
            MergeSort(A,q+1,r);			//将右半边排序
            Merge(A,p,q,r);				//归并结果
        }
}

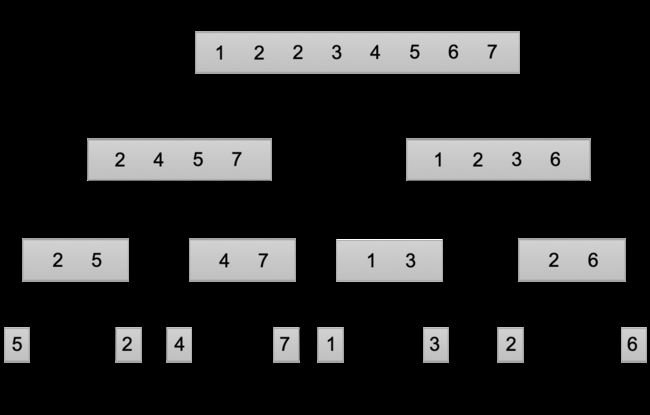
    下面我们来看一下归并排序在数组A=[5,2,4,7,1,3,2,6]上的操作，随着算法自底向上地推进，待合并的已排好序的各序列的长度不断增加。

‘-----------------------------------------------------------------’
    分治法的讲解到这里已经结束
    其他算法：算法导论——各章节算法伪代码和java实现