（北京理工嵩天）Python学习 第三周
本周将进行 python的语法
本课程将介绍六种语言类型：数字，字符串，元组，列表（本周）文件，字典（之后）
数字类型
python有三种数字类型:整数类型，浮点数类型，复数类型
整数类型
同数学，无取值范围，可二进制，十进制，十六进制等
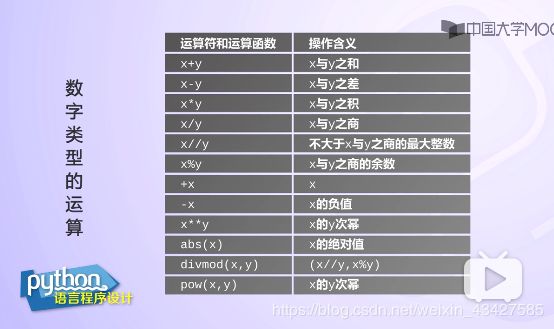
pow（x，y）：计算x^y
如pow(2,10)=1024
浮点数类型
带有小数点以及小数的数字
pyhton中浮点数数值范围有限制，小数精度也存在限制，与计算机系统有关。
在IDLE中输入可查
import sys
sys.float_info
e.g :0.0,-7.7
96e4,4.3e-3(科学计数法，e/E表示幂函数以10为底，96e4=96*10^4)
复数类型
与数学一致，z=a+bj，a,b都是浮点类型
z.real为实数部分，z.imag为虚数部分
数字类型关系
宽度有大到小：复数，浮点数，整数
可以混合运算，输出宽度最大类型如：
123+4.0=127.0
相互转换函数：
int() 函数变为整数
float() 函数变为浮点数
complex() 函数变为复数
int（4.5）=4
float(4)=4.0
complex(4)=4+oj
若要将复数转换为浮点数或整数，可以用imag和real函数将实部与虚部先进行转换
type()函数用于输出函数类型
运算
字符串
用双引号或单引号括起来的字符str1=“Hello”,str2=‘John’
转义符 \ 用于输出带引号的字符串 如 “‘John’\”
字符串类型
索引：编号随着字符序列从0开始，从左到右依次增加
单个索引 访问字符串中特定位置
>>> greet="Hello honey"
>>> print(greet[2])
l
>>> x=8
>>> print(greet[x-2])
h
因为索引是从0开始，所以对于长度为L的字符串，最后一个字符位置为L-1
也可以使用负数从右向左反向索引，最右侧索引值是-1，如
>>> greet[-1]
'y'
也可以通过
start&end都是整数型，子序列从索引start开始到end结束，不包含end位置，（位数是end-start）如
>>> greet[0:3]
'Hel'
字符串之间可以用+，进行连接
“+”可以将两个字符串连接成一个新字符串
“”可以构建一个从本身重复连接而成的新字符串如
>>> "pine"+"apple"
'pineapple'
>>> 3*"pine"
'pinepinepine'
>>>
len()函数可以返回字符串长度
>>> len("pine")
4
>>> len("刘cx真帅")
5
大多数数据类型都可以使用str()函数转换为字符串
e.g 输入一个月份数字返回对应月份名称缩写
IPO模式：
I：输入一个表示月份的数字（1-12）
P：利用字符串基本操作实现该功能（处理）
O：输入数字对应月份名称缩写
(输入的月份数-1)*3便是月份的起始位置
# month.py
months="JanFebMarAprMayJunJulAugSepOctNovDec"
n=input("请输入月份数（1-12):")
pos=(int(n)-1)*3
monthAbbrev=months[pos:pos+3]
print("月份缩写是"+monthAbbrev+".")
>>>
请输入月份数（1-12):6
月份缩写是Jun.
>>>
将其改编成通过数字1-7返回中文的星期一到星期天，程序如下：
# day.py
days="星期一星期二星期三星期四星期五星期六星期天"
n=input("请输入一周的某天数（1-7）：")
pos=(int(n)-1)*3
dayAbbrev=days[pos:pos+3]
print("中文描述是"+dayAbbrev)
>>>
请输入一周的某天数（1-7）：7
中文描述是星期天
>>>
字符串操作方法采用格式
.func()
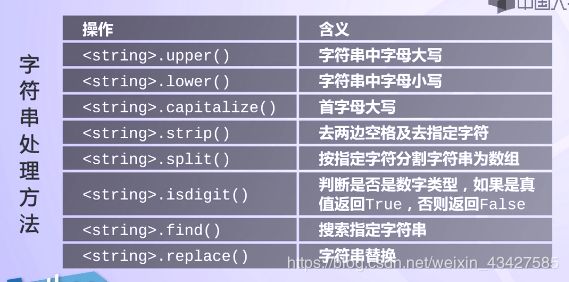
循环遍历字符串中每个字符
forin:
元组类型 （tuple）
元组的概念
元组的三个特点
1.元组中的元素可以是不同类型，也可以成为别的元组元素（用括号隔开）
如：t3=123,456,(“hello”,“中国”)
2.元组中各个元素存在先后关系，可以通过索引访问元组中的元素
如：t3[0]
3.元组定义后不能更改，也不能删除
如：t3[0]=456
元组概念
元组类型定以后无法更改，程序代码更加安全。若要灵活性，可以使用下面的列表类型。
列表类型
列表的概念
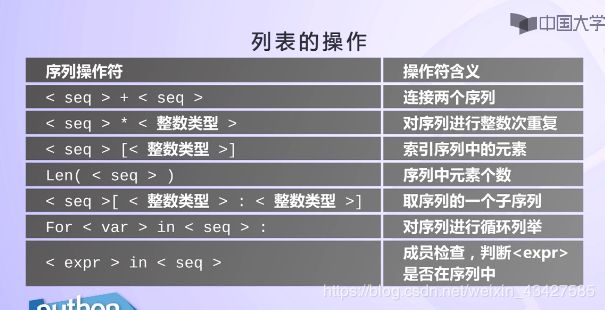
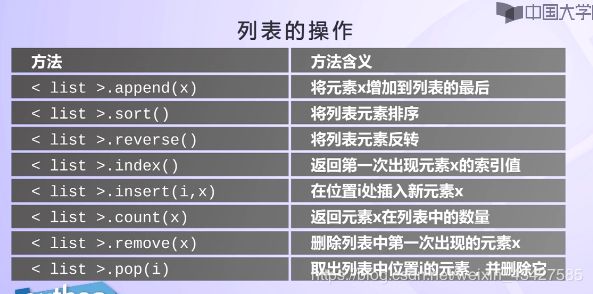
列表的操作
e.g
>>> vlist=[0,1,2,3,4]
>>> vlist*2
[0, 1, 2, 3, 4, 0, 1, 2, 3, 4]
>>> len(vlist[2:])
3
>>> for i in vlist[3:]:
print(i)
3
4
>>> 2 in vlist
True
>>>
>>> vlist=[0,1,2,3,4]
>>> vlist.append('python')
>>> vlist
[0, 1, 2, 3, 4, 'python']
>>> vlist.reverse() #元素反转
>>> vlist
['python', 4, 3, 2, 1, 0]
>>> vlist.index(3) #出现3时第一次位置
2
>>> vlist.pop(2) #取出位置2的元素并删除
3
>>> vlist
['python', 4, 2, 1, 0]
>>>
math库&random库
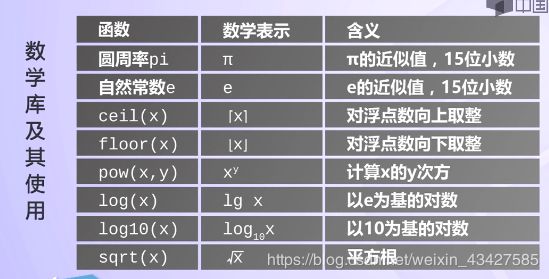
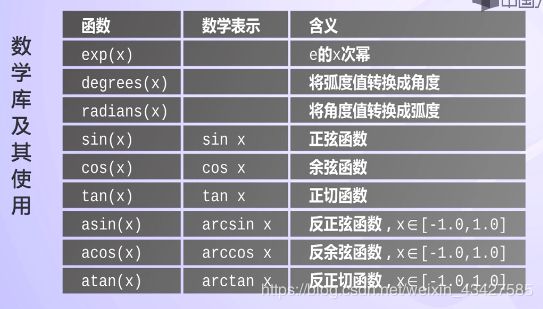
数学库及其应用
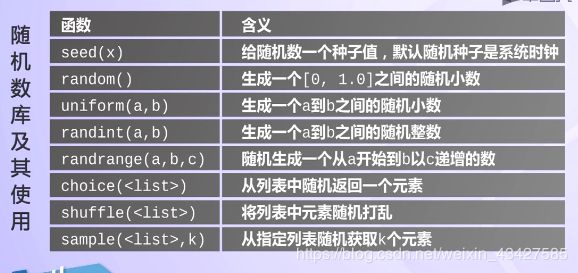
随机数库及其应用
>>> from random import * #引入random库
>>> random()
0.7546579109324009
>>> from random import * #引入random库
>>> random() #0-1之间随机生成一个小数
0.21320738865725752
>>> uniform(1,10) #1-10之间随机生成一个小数
2.7809679443112936
>>> randint(1,10) #1-10之间随机生成一个整数
5
>>> randrange(0,10,2) #生成一个列表
4
>>> ra=[0,1,2,3,4,5,6,7,8,9]
>>> choice(ra) #列表中随机生成一个数
1
>>> shuffle(ra) #随机改变列表的顺序
>>> ra
[8, 9, 6, 2, 4, 1, 3, 7, 5, 0]
>>> samole(ra,4) #在列表中随机采样四个元素
Traceback (most recent call last):
File "", line 1, in
samole(ra,4) #在列表中随机采样四个元素
NameError: name 'samole' is not defined
>>> sample(ra,4) #列表中随机采样四个元素
[1, 4, 6, 7]
>>>
之前的例子，random自动利用系统时钟作为种子，但其实计算机的随机都是伪随机，如我们不论设定几次seed（10）结果都会相同
π的计算实例
蒙特卡洛（MonteCarlo方法）又称随机抽样或统计试验方法。当所求解的问题是某种事件出现的概率或某随机变量的期望时可以通过某种“试验”的方法求解。
简单来说MonteCarlo是利用随机试验求解问题的方法。
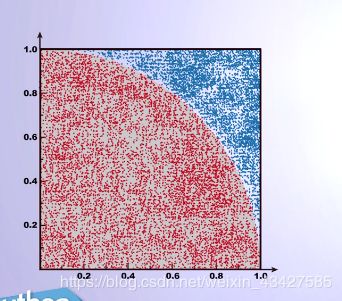π计算的IPO
输入：抛点的数量
处理：对于每个抛洒点，计算点到圆心的距离，通过距离判断该店是否在圆内或者圆外。统计在圆内点的数量。
输出：π值
需要数学库和随机库，引入time库进行计时。
该图中1/4圆中抛洒点数量与单位正方形中总抛洒点数量的比值极为1/4圆的面积，即1/4π。
程序如下：
# pi.py
from random import random
from math import sqrt
from time import process_time
DARTS = 2**23 #输入部分，darts表示抛洒点数量，当超过2^30次方时将会非常精确了
hits=0
process_time()
for i in range(1,DARTS): #操作部分，主体是一个循环，模拟抛洒点过程，每个抛洒点的内部是一个抛洒点的处理
x,y=random(),random() #给予x,y随机的坐标值
dist=sqrt(x**2+y**2) #sqrt开方函数 求出x,y到原点的距离
if dist <=1.0: #if语句判断该点处于圆内或圆外，圆内及+1圆内数
hits=hits + 1
pi=4*(hits/DARTS) #最终，根据总抛点数落入圆内的数量计算比值，从而得到π
print("Pi的值是%s"%pi) #输出部分
print("程序的运行时间是%-5.5ss"%process_time())
>>>
====================== RESTART: E:/Python/代码目录/π值得计算.py ======================
Pi的值是3.1407546997070312
程序的运行时间是8.421s