机器学习之逻辑回归

一、前言：
logistic回归又称为逻辑回归，是经典的二分类算法，虽然其名称中含有“回归”一词，但其并不是用于回归，而是主要用于分类，其决策边界可以是非线性的。
二、Sigmoid函数

• 公式：
  $$g(z)=\frac{1}{1+e^{(-z)}}\text{\hspace{1em}(1)}$$
  其中·e为欧拉常数，$z$为自变量（实际为样本特征值的线性组合），$z=W^{T}X=w_0{x}_0+w_1{x}_1+...+w_n{x}_n$。
• 函数图像：
  
• 函数特点：Sigmoid函数定义域为[-$\infty$,+$\infty$]，值域为[0,1]，即无论输入任何值$z$，总可以将结果映射到0~1区间内，很明显它可以作为概率分类。

三、推导
假设我们有1 * m个样本为$Y$，则:
$$Y=\left[\begin{array}{cccc}{y}_0& y_1& ...& y_n\end{array}\right]$$
$y_0、y_1、y_2、...、y_n$分别为每个样本值。

设有n * m 的特征矩阵为$X$:

$$X=\left|\begin{array}{cccc}{x}_{11}& x_{12}& ...& x_{1m}\\ x_{21}& x_{22}& ...& x_{2m}\\ ⋮& ⋮& ...& ⋮\\ x_{n1}& x_{n2}& ...& x_{nm}\end{array}\right|$$
$x_{i1}、x_{i2}、...、x_{im}$为每个样本的特征值。
一般为了得到偏置项$w_0$，我们一般在特征矩阵加一列$x_{i0}$，一般将$x_{i0}$设为1，则得到n * m+1 的特征矩阵$X$:
$$X=\left|\begin{array}{ccccc}1& x_{11}& x_{12}& ...& x_{1m}\\ 1& x_{21}& x_{22}& ...& x_{2m}\\ ⋮& ⋮& ⋮& ...& ⋮\\ 1& x_{n1}& x_{n2}& ...& x_{nm}\end{array}\right|$$
提醒一下，矩阵是从下标$x_{i0}$开始，这里从$x_{i0}$开始，为了方便看成矩阵。

则参数为1 * m+1的矩阵$W$:
$$W=\left[\begin{array}{cccc}{w}_0& w_1& ...& w_m\end{array}\right]$$
$w_1、w_2、...、w_m$为权重系数，$w_0$为偏置项，（一般称为截距）

三、如何将数据进行分类？

通过将每个样本的特征$x_i$乘以一个回归参数$w_i$，求和得$h_w(x_i)$，则：
$$h_w(x_i)=W{X}_i^T=w_0{x}_{i0}+w_1{x}_{i1}+...+w_m{x}_{im}\text{，单个样本}\text{\hspace{1em}(2)}$$
其中·$h_w(x_i)$表示第$i$个样本的特征$x_i$与$w_i$的线性和，$i\in \{1、2、...、n\}$，因为总共n个样本。

将每个样本的线性特征的累加和$h_w(x_i)$，作为自变量$z_i$带入Sigmoid函数：
由题知：$$z_i=h_w(x_i)\text{\hspace{1em}(3)}$$
带入$h_w(x_i)$：
$$g_w(z_i)=(h_w(x_i))=\frac{1}{1+e^{-h_w(x_i)}}$$
为了便于推导理解，我们有：
$$p_w(x_i)=g_w(z_i)$$
$p_w(z_i)$表示每个样本的概率值，范围为[0，1]，这样我们就将$h_w(x_i)$映射到[0,1]区间上了。
为了便于以后计算我们把所有的样本$h_w(x_i)$用一个矩阵$h_w(x)$来表示,即：
$$h_w(x)=W{X}^T=\left[\begin{array}{cccc}{h}_w(x_1)& h_w(x_2)& ...& h_w(x_n)\end{array}\right]$$
四、由样本值到概率的的转换
      我们将每个样本值$h_w(x_i)$作为自变量带入Sigmoid函数中，$h_w(x_i)$被映射到了[0,1]区间，这样就完成了由值到概率的转换，假设我们取阈值为0.5，则任何大于0.5的数据被归为1类，小于0.5的数据被分归为0类，所以logistic回归也可以看成一种概率估计，根据题意知$z_i=h_w(x_i)$。
$$p_w(x_i)=g(h_w(x_i))=\frac{1}{1+e^{(-h_w(x_i))}}\text{\hspace{1em}(3)}$$
这里$p_w(x)$为预测值，范围为0~1之间

根据Sigmoid图形可以看出，根据$p_w(x_i)$的不同，可分为三种情况：
$$p_w(x)=\{\begin{array}{ll}{p}_w(x_i)>0.5，& \text{hw(xi) > 0，归为1类}\\ p_w(x_i)=0.5，& \text{hw(xi) = 0，称为决策边界}\\ p_w(x_i)<0.5，& \text{hw(xi) < 0，归为0类}\end{array}$$
这里$i\in \{1，2，...,n\}$表示第$i$个样本的概率值.

当样本值$h_w(x_i)=W{X}_i^T=w_0{x}_{i0}+w_1{x}_{i1}+...+w_m{x}_{im}=0$时，
$$p(0)=\frac{1}{1+e^{(-0)}}=\frac{1}{2}=0.5$$
$p(z)$ = 0.5，即表示该样本既不属于1类也不属于0类，称为决策边界，我们一般用它来区分0类和1类。利用logistic函数最终求的结果只有两种可能要么是有y = 0类要么是y = 1类，这里的y表示样本的类别标签，$p(z_i)$表示y为0类或1类的概率。
从而我们假设y = 1或y = 0得概率分别为：
$$P(y_i=1|x_{,}w)=h_w(x_i)\text{，表示为1类的概率}$$
$$P(y_i=0|x_i,w)=1-h_w(x_i)\text{，表示为0类的概率}$$
这里$y_i$表示第$i$个样本的类别标签，只有0或1两种可能，$h_w(x_i)$表示第$i$个样本为1类的概率大小，则$1-h_w(x_i)$为0类的概率，则$x_i$表示第$i$个样本的特征值，$w$表示参数矩阵，

由题意可知$y_i$要么等于0，要么等于1：
$$P(y_i|x_i,w)=\{\begin{array}{ll}{p}_w(x_i),& \text{当yi = 1时，表示为1类的概率}\\ 1-p_w(x_i),& \text{当yi = 0时，表示为0类的概率}\end{array}$$
为了便于求解我们将上式整合下面：
$$P(y_i|x_i,w)={（h_w(x_i)）}^{y_i}（1-h_w(x_i){）}^{1-y_i}$$
五、Logistic回归的优缺点：
优点：计算代价不高，易于理解和实现。
缺点：容易欠拟合，分类精度可能不高。

六、最大似然函数
说到这里，我们就是希望找到一组参数$w$，使$p_w(x_i)$预测得总体正确率最高，根据最大似然估计（这里涉及到概率论知识）就是所有样本预测正确的概率$p_w(x_i)$相乘得到的总体$P(y_i|x_i,w)$正确概率最大。
于是我们就得到$最大似然估计$：
$$l(w)=\frac{1}{n}\prod _{i=1}^{n}P(y_i|x_i,w)=\frac{1}{n}\prod _{i=1}^n{(p_w(x_i))}^{y_i}{（1-p_w(x_i)）}^{1-y_i}$$
其中，$y(x_i)$为根据参数$w$和特征值$x$预测出的分类标识。$y_i\in \{0,1\}$ ，似然函数表示预测值正确的概率值，当似然函数的概率值最大时，即预测正确的可能性越高，$w$的值最优，还要注意我们的代价函数不管是最小二乘法、误差均方、似然函数等，都要求平均，就是前面加上$\frac{1}{n}$。

对于这种函数我们很难求解，所以要对其求对数得到$对数似然函数$：
$$L(w)=logl(w)=\frac{1}{n}\sum _{i=1}^n{y}_{i}log(p_w(x_i))-(1-y_i)log(1-p_w(x_i))$$注意：到这就变成了求出对数似然的概率最大值。

我们本次主要使用梯度下降法求解参数W，前面要加个负号，即求对数依然的最小值，所以：
$$L(w)=\frac{1}{n}\sum _{i=1}^n(-y_{i}log(p_w(x_i))-(1-y)log(1-p_w(x_i))$$
这个函数就是我们逻辑回归(logistics regression)的损失函数,我们叫它交叉熵损失函数,logistic回归问题就是根据训练样本求解代价函数在取得最小值的参数问题，此时有参数确定的分类界限可将两类样本相对准确的分开。
七、求解交叉熵损失函数
求损失函数的梯度部分同样是对损失函数求偏导，注意在求偏导时我们求的是梯度的累加和,所以我们要乘以$1/n$来取梯度的均值，考虑总体样本， （错误想法），（$L(w)$为代价函数求解出来的偏导就是其梯度，不存在累加和什么的，只存在$1/n$考虑总体样本）过程如下：（求解的偏导是关于$w$的梯度，表示$w$的梯度方向和倾斜程度）

我们注意到这个迭代公式和线性回归的迭代公式形式是一样的，只是在线性回归中$h_w(x_i)$为$x_i$的各维度线性叠加即$h_w(x_i)=W^T{x}_i$，而这里逻辑回归$x_i$的各维度线性叠加$W^T{x}_i$以后，还要进行一次非线性映射（即logistic映射），非线性的映射到（0,1）之间即$p_w(x_i)$。所以也可以认为logstic回归也是处理的线性问题，即也是求的各维度线性叠加的权重系数，只是求得了各维度线性叠加和以后，不是与$x_i$所属的类别$y_i$进行比较，而是非线性映射到所属类别的概率$p_w(x_i)$，然后最大似然函数法求模型参数$w$（也就是那个各维度线性叠加的权重，而后面的非线性映射logstic那里没有参数），回归过程大概可以表示为：
逻辑回归主要过程：$z=h_w(x)=W^{T}X$，$p_w(x)=g（z)=g(h_w(x))$，即得出的特征与参数的线性组合$h_w(x)$要带入Sigmoid函数，映射到[0,1]内，
而线性回归的过程：$h_w(x)=W^{T}X$。
$w$参数更新：
$$\begin{gathered} w_{i+1}=w_i-\alpha \frac{1}{n}\sum _{i=1}^m(p_w(x_i)-y_i)x_i^j \\ i\in \{1，2，...,n\}，j\in \{0，1，2，...，m\} \end{gathered}$$
$\alpha$为梯度下降学习率即步长，$w_i$为当前位置，$w_{i+1}$为梯度的下一个位置，$y_i$表示样本的真实标签，也就是第$i$个样本所属的类别（0或1），$p_w(x_i)$表示的是回归模型预测的第i个样本向量为1的概率，$x_i^j$表示样本$x_i$的第k个分量，并设$x_i^0=1$，
在这里要解释，对于求出的梯度值$$\frac{1}{n}\sum _{i=1}^m(p_w(x_i)-y_i)x_i^j$$
表示所有样本在权重为$w$时的梯度之和并求均值目的是考虑整体样本，梯度的正负表示梯度的方向，梯度的模表示梯度的倾斜程度以及长度，乘以$\alpha$学习率表示每次下降的步长，$\frac{1}{n}$可以不带，不影响求解。
所以权重的迭代更新公式为：
$$w_{i+1}=w_1-step\ast \sum _{i=1}^m(p_w(x_i)-y_i)x_i^j$$
可以写成下面形式：
$$w_{i+1}=w_1-step\ast gradien{t}_w$$
更新梯度值由$w_i$到$w_i+1$，$gradien{t}_w$表示梯度方向和倾斜程度，$w_1$不断减去梯度的方向，想象一个三维凹函数，不断地迭代，$w_i$的值不断地更新，一直往下降,$w$ 值朝着梯度方向不断迭代。


七、代码精讲
下面我们说一个例子，通过sklearn库中datasets的API中的函数make_moons我们生成一个1000 * 2的矩阵$x$，1 * 1000的矩阵$y$，其中$y\in \{0，1\}$，假设y的值由x值确定，求$y=w_0{x}_0+w_1{x}_1+w_2{x}_2$中，$w_0、w_1、w_2$的值,其中$x_0=1$
首先生成实验数据

#生成实验数据
from sklearn.datasets import make_moons
import matplotlib as mpl
import matplotlib.pyplot as plt
x, y = make_moons(1000, noise = 0.3) #生成月亮形状的数据
cm_pt=mpl.colors.ListedColormap(['w', 'g']) #设置颜色映射
plt.scatter(x[:,0],x[:,1],c=y, cmap=cm_pt, marker='o',edgecolors='k')
plt.show()

2、定义Logistic回归类

#2.定义Logistic回归类
class LR:
    def __init__(self):
        self.w = np.zeros(3) #初始参数[w0,w1,w2] = [0,0,0]，
    #表示样本Xi各个元素叠加的权重系数，这里以向量形式表示，且初始都为0，三维向量
        self.step = 0.2 #学习率alpha
    def sigmoid(self, x): #sigmoid映射函数,值域-->[0,1],定义域-->[-infity,+infity]
        return 1.0/(1+np.exp(-x))
    def logistic_regression(self,x,y,step):#Logistic函数,核心
        iter = 0#迭代计数
        self.step = step #设置步长
        row=np.shape(x)[0] #样本数row = 1000
        while iter <= 1000: #迭代1000次（可设置）
            #求取梯度
            X = np.hstack([np.ones([row,1]),x]) #为求偏置项w0，特征矩阵第一列为1
            fx = np.dot(self.w, X.T) #求出参数特征值的线性组合[h(x1),h(x2),...,h(xn)]。
            #fx是一个列向量，每一个元素是每一个样本Xi的线性叠加和，因为X是所有的样本，因此这里不是一个一个样本算的，而是所有样本一块算的，因此fx是一个包含所有样本Xi的线性叠加和的向量。在公式中，是单个样本表示法，而在matlab中都是所有的样本一块来。
            hx = self.sigmoid(fx) #调用Sigmoid函数使h(x_i)映射到区间[0,1]范围内,这个hx就是样本Xi所对应的yi=1时，映射的概率。如果一个样本Xi所对应的yi=0时，对应的映射概率写成1-h。
            hx_y = (hx-y) #求出预测值与真实值概率的差值
            hx_y_ext = np.vstack([hx_y.T, hx_y.T, hx_y.T]).T #在水平方向上连接矩阵
            s = np.multiply(hx_y_ext,X) #表示矩阵对应元素相乘
            gradient_w = np.mean(s, 0) #求和平取均值，求出损失函数L(x)
            #更新参数
            self.w -= self.step * gradient_w #更新梯度值由w_i到w_i+1
            iter += 1 #计算迭代次数。

#3.实验结果：

lr = LR() #logistic类实例化
lr.logistic_regression(x,y,step = 0.5) #logistic回归
print(lr.w)#输出参数[w0,w1,w2]


-->[w0,w1,w2]=[0.28848812  1.29301211 -3.74713688]

那么问题来了，如何画出分类界限？
对于两分类问题，当$p_w(x)>0.5$时将样本$x$归为$1$类，当$p_w(x)>0.5$时将样本$x$归为$0$类，因此当$p_w(x)=0.5$时，为分类界限既不属于$0$类也不属于$1$类。
$$\begin{gathered} p_w(x)=\frac{1}{1+e^{(-h_w(x)=0)}} \\ =\frac{1}{1+e^{(0)}} \\ =\frac{1}{2}=0.5 \end{gathered}$$
可以看出当$h_w(x)=w_0{x}_0{w}_1{x}_1+w_2{x}_2+...+w_n{x}_n=0$时，$p_w(x)=0.5$，可根据分类界限，绘制相应的分类直线。
所以根据上述公式，当$p(x)=0.5$时，为分类界限，此时$h_w(x)=w_0{x}_0+w_1{x}_1+w_2{x}_2=0$，又因为$x_0=1$，$w_0$为偏置项，所以解方程可得：
$$x_2=(w_0+w_1{x}_1)/w_2$$如果不理解可以将$x_2$也可以看成一元一次方程的$y$，他是特征值$x_1$关于$x_2$的方程。

1、我们解出来以后发现，这个方程是一个直线方程：$w_1{x}_1+w_1{x}_{1}x2+w_2{x}_2=0$ ，注意我们不能因为这个分界面是直线，就认为logistic回归是一个线性分类器，注意logistic回归不是一个分类器，他没有分类的功能，这个logistic回归是用来预测概率的，这里具有分类功能是因为我们硬性规定了一个分类标准：把$p_w(x_i)>0.5$的归为一类，$p_w(x_i)<0.5$的归于另一类。这是一个很强的假设，因为本来我们可能预测了一个样本所属某个类别的概率是0.6，这是一个不怎么高的概率，但是我们还是把它预测为这个类别，只因为它$p_w(x_i)>0.5$.所以最后可能logistic回归加上这个假设以后形成的分类器的分界面对样本分类效果不是很好，这不能怪logistic回归，因为logistic回归本质不是用来分类的，而是求的概率。
2、那么分界面怎么画呢？
问题也就是在$x1$，$x2$坐标图中找到那些将$w_1{x}_{1}1$，$w_2{x}_2$带入$\frac{1}{(1+exp(-wx))}$后，使其值$p_w(x_i)>0.5$的（x1,x2）坐标形成的区域，因为我们知道$\frac{1}{(1+exp(-wx))}>0.5$意味着该区域的（x1，x2）表示为1类的概率大于0.5,那么其他的区域就是0类，那么$\frac{1}{(1+exp(-wx))}=0.5$解出来的一个就是关于x1，x2的方程就是那个分界面。我们解出来以后发现，这个方程是一个直线方程：$w_1{x}_1+w_1{x}_{1}x2+w_2{x}_2=0$ 注意我们不能因为这个分界面是直线，就认为logistic回归是一个线性分类器，注意logistic回归不是一个分类器，他没有分类的功能，这个logistic回归是用来预测概率的，这里具有分类功能是因为我们硬性规定了一个分类标准：把>0.5的归为一类，<0.5的归于另一类。这是一个很强的假设，因为本来我们可能预测了一个样本所属某个类别的概率是0.6，这是一个不怎么高的概率，但是我们还是把它预测为这个类别，只因为它>0.5，所以最后可能logistic回归加上这个假设以后形成的分类器的分界面对样本分类效果不是很好，这不能怪logistic回归，因为logistic回归本质不是用来分类的，而是求的概率。

于是得到下面代码：

#定义结果显示函数如下 
def show_result(self):#显示结果
        x1 = np.linspace(-1, 2)
        cm_pt=mpl.colors.ListedColormap(['w', 'g']) #设置颜色映射
        plt.scatter(x[:,0],x[:,1],c=y,cmap=cm_pt,marker='o',edgecolors='k')  
        x2 = (self.w[1] * x1 + self.w[0])/(-self.w[2]) #根据p = 0.5所得,h(x) = 0解的方程。
        plt.plot(x1,x2,'b-',linewidth=2)
        plt.show()

#显示函数调用：
lr.show_result()

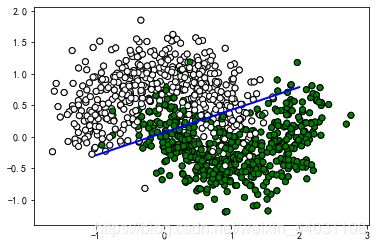
那么问题又来了如何根据样本预测该样本的类别？
很简单，按照上面的思路推就出来了，第一步根据所得特征值$x$，乘以参数$w$得到$h_w(x)$带入Sigmoid函数，求得所得的概率$p_w(x)$，当$p_w(x)>0.5$时将样本$x$归为$1$类，当$p_w(x)>0.5$时将样本$x$归为$0$类，因此当$p_w(x)=0.5$时，该样本正好处于分类界限位置，他既不属于$0$类也不属于$1$类。

def predict(self,x): #预测
        row=np.shape(x)[0] #样本数
        X = np.hstack([np.ones([row,1]),x])
        fx = np.dot(self.w, X.T) #求代价函数梯度
        P = self.sigmoid(fx) #sigmoid函数输出值
        #利用阈值0.5进行分类
        C = P.copy() #复制P值指向另一个内存，修改其值并不影响P值。
        C[C >= 0.5] = 1
        C[C < 0.5] = 0      
        return P, C
#显示函数调用：
P, C = lr.predict(x[1:5,:])  #预测4个样本的类别
print(P) #=> [ 0.9930546   0.21428264  0.01606024  0.69586661] #概率
print(C) #=> [ 1.  0.  0.  1.] #类别

整体代码：

from sklearn.datasets import make_moons
x, y = make_moons(1000, noise = 0.3) #产生数据

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
cm_pt=mpl.colors.ListedColormap(['w', 'g']) #设置颜色映射
plt.scatter(x[:,0],x[:,1],c=y, cmap=cm_pt, marker='o',edgecolors='k')
#plt.show()
#2.定义Logistic回归类
class LR:
    def __init__(self):
        self.w = np.zeros(3) #初始参数[w0,w1,w2]
        self.step = 0.2 #学习率
    def sigmoid(self, x): #sigmoid函数
#        print(x)
        return 1.0/(1+np.exp(-x))

    def logistic_regression(self,x,y,step):#Logistic函数
            iter = 0#迭代计数
            self.step = step #设置步长
            row=np.shape(x)[0] #样本数
            while iter <= 1: #迭代1000次（可设置）
                #求取梯度
                X = np.hstack([np.ones([row,1]),x])
                fx = np.dot(self.w, X.T)
#                print(fx)
                hx = self.sigmoid(fx)
#                print(hx)
                hx_y = (hx-y)
                hx_y_ext = np.vstack([hx_y.T, hx_y.T, hx_y.T]).T
#                print(X.shape)
                s = np.multiply(hx_y_ext,X) #矩阵对应位置相乘即样本的各个分量相乘
                gradient_w = np.mean(s, 0) #axis = 0压缩行，对各列求和并取均值,求取梯度的均值，返回 3*1 矩阵
                #更新参数
                self.w -= self.step * gradient_w #利用梯度值，更新W参数值
                iter += 1
#定义结果显示函数如下 
    def show_result(self,a):#显示结果
            x1 = np.linspace(-1, 2)
#            ro=np.shape(x1)[0] #样本数
            cm_pt=mpl.colors.ListedColormap(['w', 'g']) #设置颜色映射
            plt.scatter(x[:,0],x[:,1],c=y,cmap=cm_pt,marker='o',edgecolors='k')
#            print(a.shape,ro)
#            x2 = np.dot(self.w,np.hstack([np.ones([ro,1]),a]).T)
            
            x2 = (self.w[1] * x1 + self.w[0])/(-self.w[2])
            plt.plot(x1,x2,'b-',linewidth=2)
            plt.show()
    #预测样本
    def predict(self,x): #预测
            row=np.shape(x)[0] #样本数
            X = np.hstack([np.ones([row,1]),x])
            fx = np.dot(self.w, X.T)
            P = self.sigmoid(fx) #sigmoid函数输出值
            #利用阈值0.5进行分类
            C = P.copy() #复制P的内容，使其指向另一个内存
            C[C >= 0.5] = 1
            C[C < 0.5] = 0      
            return P, C
#3.实验结果：
lr = LR() #logistic类实例化
lr.logistic_regression(x,y,step = 0.5) #logistic回归
#print("参数w：",lr.w)#输出参数[w0,w1,w2]


a, b = make_moons(50, noise = 0.3) #产生数据
#显示函数调用：
lr.show_result(a)

#[w0,w1,w2]=[0.28848812  1.29301211 -3.74713688]

#显示函数调用：
P, C = lr.predict(x[1:5,:])  #预测4个样本的类别
print("参数w：",lr.w)#输出参数[w0,w1,w2]
print("概率P:",P) # => [ 0.9930546   0.21428264  0.01606024  0.69586661] #概率
print("类别C：",C) #=> [ 1.  0.  0.  1.] #类别

结果：

参数w： [-0.00455566  0.2295211  -0.18620505]
概率P: [0.50581431 0.55949027 0.59123491 0.45818361]
类别C： [1. 1. 1. 0.]

参考链接：
1 - ->Logistic回归深入理解和matlab程序注释 -->新浪
2 - ->机器学习实战之Logistic回归
3 - ->Logistic回归 机器学习
4 - ->解释logistic回归为什么要使用sigmoid函数
5 - ->逻辑回归(logistics regression)
6 - - >梯度下降法
7 - ->机器学习逻辑回归
8 - - >机器学习logistic回归
9- - >Logistic回归
梯度下降法的三种形式BGD、SGD以及MBGD
线性回归、logistic回归、广义线性模型

10 - ->logistic