CMOS:MOS电容
MOS电容是晶体管的重要组成部分,与pn结相同,MOS电容也拥有两个端口
通过了解MOS电容,我们可以更好地理解MOSFET的特性
1. 物理结构
MOS电容可以分为三层
上层是金属制成的栅电极(gate)
下层是半导体制成的基极(substrate)
中间层填充了氧化物,通常为SiO2
它只有 gate 和 substrate 两个端口
示意图如下:

2. 能带图
2.1 硅基极能带图
为了更好的理解MOS电容,我们需要分析几组能带图,硅基级最上层的能带并非导带,而是自由空间能级(free space energy level),或称真空能级(vacuum),如果有粒子到达这个能级,它就会从我们的材料中脱出,示意图如下:
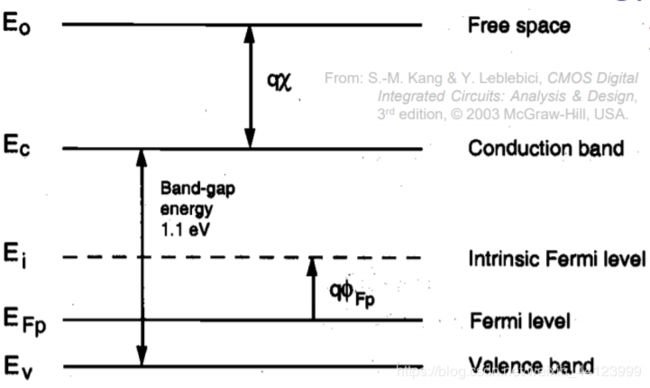
2.1.1 费米势
在掺杂半导体中,平衡后的费米能级与本征费米能级之间的关系可以通过如下方式计算:
ϕ F ≡ E F − E i q \phi_F\equiv \frac{E_F-E_i}{q} ϕF≡qEF−Ei
注意这里的是恒等于号
当费米能级靠近导带时:
ϕ F p = k T q l n ( n i p ) ≈ k T q l n ( n i N A ) \phi_{Fp}=\frac{kT}{q}ln(\frac{n_i}{p})\approx \frac{kT}{q}ln(\frac{n_i}{N_A}) ϕFp=qkTln(pni)≈qkTln(NAni)
当费米能级靠近价带时:
ϕ F n = k T q l n ( n n i ) ≈ k T q l n ( N D n i ) \phi_{Fn}=\frac{kT}{q}ln(\frac{n}{n_i})\approx \frac{kT}{q}ln(\frac{N_D}{n_i}) ϕFn=qkTln(nin)≈qkTln(niND)
因此,我们可以用 ϕ F \phi_F ϕF来定义MOS的状态,比如倒置(inversion)
2.2 三种材料的独立能级
如果我们把MOS电容的三部分分开来看,他们的能带图如下所示:

三种材料的能带图都是用真空能级 E 0 E_0 E0作为参考,本图中的材料是独立的,相互之间没有影响
2.2.1 逸出功
对于金属层,它的费米能级 E F m E_{Fm} EFm与真空能级 E 0 E_0 E0之间的能量差称为逸出功,也叫功函数(work function)
逸出功的表达式为 q ϕ q\phi qϕ,常用单位为电子伏特(eV)
2.3 三种材料的联合能级
当三种材料连在一起,其中金属层和 p-type 半导体层的费米能级将统一到同一水平线,此时的能带图如下所示:
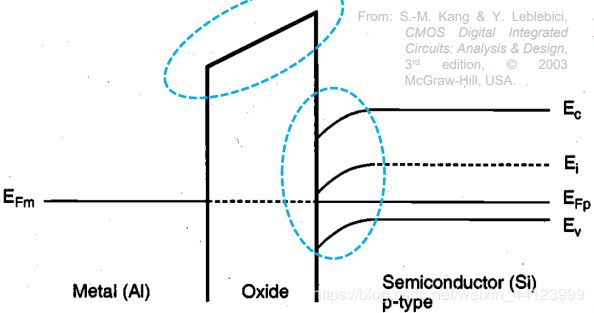
这张图中最需要注意的是氧化物层和氧化物-半导体曾交界处的能带弯曲
其中氧化物层最上面的能带是真空能级,这一能级的倾斜可以表现出半导体层和金属层的能带情况,比如本图中,真空能级向右上倾斜,则代表此时的半导体导带和价带要高于金属的导带和价带。
3. 工作模式
在初步了解了MOS电容的能带图之后,我们将从不同角度分析MOS电容的工作模式
3.1 Accumulation mode
如果我们给gate一个反向电压 V G V_G VG,如图所示:

可以看到,由于电压的推动,此时基极内的空穴都向氧化物层汇聚,能带图变化为:
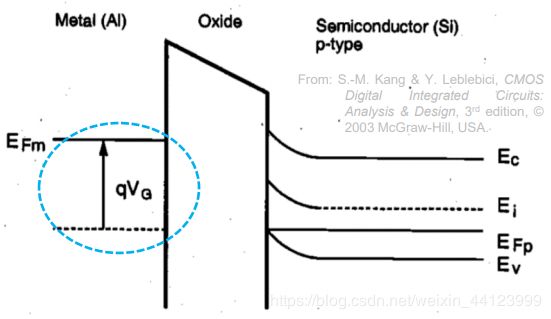
由于金属层空穴增多,它能级提高了 q V G qV_G qVG,但是半导体层的费米能级保持不变,由于中间氧化层的缘故,金属层和半导体层的能级并不一定需要统一
在半导体层,费米能级与价带能级接近,这是因为大量空穴聚集在了半导体的表面,导致那里的电子浓度降低
那么,如果我们给gate一个正向电压,又会发生什么呢?
3.2 Depletion mode
V G > 0 V_G>0 VG>0时,电场从gate指向substrate,金属层的费米能级降低,聚集在p-type半导体表层的空穴会耗尽,使得此时的半导体层费米能级接近本征半导体的费米能级,能带图如图所示:

刚才的accumulation mode中,反向的电压会使得空穴聚集在半导体层表面,那么为什么施加正向电压时电子不会聚集在表面,而只是接近本征半导体呢?这是因为我们施加的正向电压还不够大
3.3 Weak inversion
如果正向电压 V G V_G VG足够大,MOS电容就会进入弱反型模式,,此时p-type半导体层的表面反而会表现出n-type的性质,能级图如下:

可以看到,半导体层费米能级已经超过了本征费米能级
3.4 Strong inversion
继续增大我们的 V G V_G VG,MOS电容会呈现强反型状态,能带图如下:
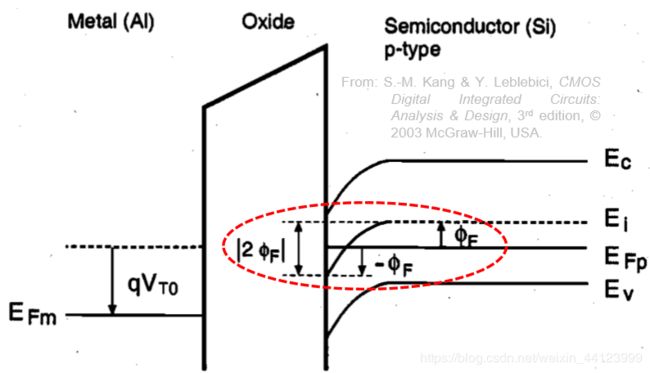
强反型的判定标准是:半导体层表面的费米能级与本征费米能级之差,等于本身p-type半导体费米能级最大值与本征费米能级之差
可以看到,正常p-type的 E i − E F p = ϕ F E_i-E_{Fp}=\phi_F Ei−EFp=ϕF,但是在表面却变成了 E i − E F p = − ϕ F E_i-E_{Fp}=-\phi_F Ei−EFp=−ϕF
此时我们定义表面电势(surface potential)为 ϕ S \phi_S ϕS为2倍的 ϕ F \phi_F ϕF,即
ϕ S = 2 ϕ F \phi_S=2\phi_F ϕS=2ϕF
n S = p p ≈ N A n_S=p_p\approx N_A nS=pp≈NA???
n p ≈ n i 2 / N A n_p\approx n_i^2/N_A np≈ni2/NA
???
这个能够使得 ∣ ϕ S = ∣ 2 ϕ F ∣ |\phi_S=|2\phi_F| ∣ϕS=∣2ϕF∣的电压被称为阈值电压 V T V_T VT
对于p-type的 substrate 来说,阈值电压一般是正值,对于n-type则是负值
阈值电压的完整计算公式如下:
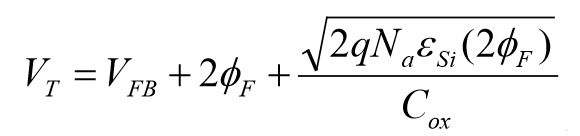
如果substrate并非接地,则公式需要改为
对于阈值电压的计算,在此仅作了解即可
4. MOS结构的电容
电容的值与MOS的工作模式相关,不同的模式下计算电容的方式不同
4.1 Accumulation and strong inversion mode
在这两种模式下,绝缘层的上下方各有电子层或空穴层,这使得MOS可以类比于一个平行板电容器,此时的电容公式为:
C = ϵ A t o x = ϵ r ϵ 0 A t o x C=\frac{\epsilon A}{t_{ox}}=\frac{\epsilon_r\epsilon_0A}{t_{ox}} C=toxϵA=toxϵrϵ0A
其中 t o x t_{ox} tox是平行板电容器之间的距离
4.2 Depletion mode
在这个模式下,不会有类似平行板电容器的结构存在,但是会出现一个类似于pn结中的耗尽区,因此,此时的电容可以用我们之前提过的pn结中的方法来计算:
C j = C j 0 1 + V R V b i C_j=\frac{C_{j0}}{\sqrt{1+\frac{V_R}{V_{bi}}}} Cj=1+VbiVRCj0
随着电压的增加,耗尽区电容会逐渐减小
同样的,耗尽区的耗尽层厚度 x d x_d xd也可以计算:
x d = 2 ϵ S i ∣ ϕ S − ϕ F ∣ q N a x_d=\sqrt{\frac{2\epsilon_{Si}|\phi_S-\phi_F|}{qN_a}} xd=qNa2ϵSi∣ϕS−ϕF∣

