多重分治和邻居传播构建高质量近邻图——CVPR论文阅读笔记
博客地址:入口
论文题目
Scalable k-NN graph construction for visual descriptors
相关信息
作者与单位
Jing Wang([email protected]); Peking University;
Jingdong Wang([email protected]); Microsoft Research Asia;
Gang Zeng([email protected]); Peking University;
Zhuowen Tu([email protected]); Microsoft Research Asia; Lab of Neuro Imaging and Department of Computer Science, UCLA;
Rui Gan([email protected]); Peking University;
Shipeng Li([email protected]); Microsoft Research Asia;
出处与时间
Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition(2019人工智能A类会议); 2012
作者拟解决的主要问题
机器学习、计算机视觉、数据挖掘、生物信息学、信息检索等领域应用数据驱动技术获得了极大的成功,其中,近邻图作为基础的组织数据的结构被广泛采用。因此,近邻图的构建长期以来得到了研究者的广泛关注。
传统的方法包括朴素或者改进的构建精确近邻图,它们的时间复杂度随维数指数级增长,随数据集的规模超线性增长,因此,不适用于大规模高维数据。现在,研究基本转向了近似近邻图的构建,比如之前介绍的NN-Descent(入口)。
之前的一些解决方案在本文中被划分为两类:一类是应用近似最近邻搜索构建近邻图,作者认为这样可能会"大材小用"了,因为近邻图构建仅仅关注数据库里面的数据点,而近似最近邻搜索要关注数据库外面的数据点。我没有理解作者这样说的原因,不过作者没有使用这种方案总要说出点它们的缺点的。目前,这种方式其实用地也很多,比如著名的HNSW。另一类便是通过分治策略构建近邻图,一般过程是将数据集迭代地划分成很多小子集,然后在小子集内构图,最后归并为一个图。现存工作归并的时候要借助重叠划分或者第三方子集,这会导致高的时间复杂度。
总之,之前的工作构图时时间复杂度太高,而得到的近邻图精度并不高,而且不适用于大规模高维场景。因此,本文沿着分治构图思路提出更好的解决方案,该方案具有高的效率和精度,而且适用于大规模图像数据集。
论文主要研究内容
如何构建一个具有高的效率和精度(是否接近精确的近邻图)且适用于大规模图像数据的近邻图,具体如下:
- 使用分治策略构建近邻图的方法;
- 多次执行随机划分提高近邻图的质量;
- 邻居传播快速提升近邻图的质量。
论文使用的方法
基本思路
本文首先使用多重随机分治方法构建基近似近邻图,把多个基近似近邻图整合到一起得到一个近似近邻图,接着,使用邻居传播方法把局部近邻传递到更宽的范围,从而快速实现一个高精度近邻图构建。
多重随机分治
使用分治的方法迭代地划分数据集,得到一个随机划分树。树的叶子结点对应数据集的一个子集,它的基数(数据点的个数)不超过一个常量,而且划分的时候尽可能使离得近的数据点划分到一个子集。本文使用的划分为不重叠划分,也就是任意两个子集的交集为 ∅ \empty ∅。在每一个叶子内部使用暴力的方式构建构建近邻图(子图),划分过程的时间复杂度为 O ( n d log n ) O(nd \log{n}) O(ndlogn),构建子图的时间复杂度为 O ( n d g ) O(ndg) O(ndg)。
注: 由于论文中并没有详细阐述划分的细节(给出方法来源的两个工作),之前的工作还未看,因此,划分过程的时间复杂度推导过程暂不列出。构建子图时,随机划分树的叶子个数为 n / g n/g n/g,每个叶子暴力构建子图时间复杂度 O ( d g 2 ) O(dg^2) O(dg2),因此,执行一次随机分治过程构建子图的时间复杂度为 O ( n d g ) O(ndg) O(ndg)。综上,执行一次随机分治的总时间复杂度为 O ( n d log n ) O(nd \log {n}) O(ndlogn)。
经过一次随机分治划分会产生 n / g n/g n/g个彼此独立的子图,一个点只可能和它所处的子图内部的点连接,不能和其它子图内部的点连接。因此,需要执行多次随机分治划分来给每个点寻找更多的邻居。为了更好理解多次随机划分的作用,考虑一个给定的点 p p p,每一次随机划分相当于枚举 p p p周围的邻居点集。我们来看图1:
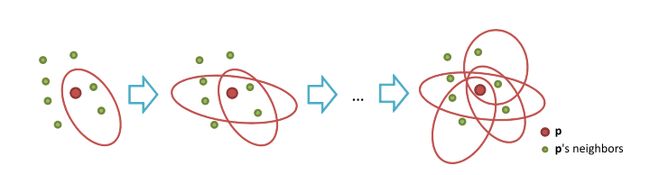
设 p p p的第 m m m次划分的邻居集为 N p m N^m _p Npm,多次划分后 p p p邻居集的并集为 N ~ p m = ⋃ i ≤ m N p i \tilde{N}^m _p=\bigcup _{i \leq m}N^i _p N~pm=⋃i≤mNpi。当增加随机划分的次数时, N ~ p m \tilde{N}^m _p N~pm将覆盖到更多 p p p的真实邻居(图1中绿色点),从而提升近邻图的质量。具体实现时,每一次划分都会得到一个基近邻图,表示为 { G 1 , … , G M } \lbrace G_1,\dots,G_M \rbrace {G1,…,GM},在图 G m G_m Gm中,点 x i x_i xi的邻接表为 A d j m [ x i ] Adj^m \lbrack x_i \rbrack Adjm[xi],经过 M M M次划分后,我们把这些邻接表并在一起,然后只保留前k个最近的邻居。
本质上,多次随机划分是利用子图之间的重叠来归并子图的。看图2,我们执行两次随机划分,第一次划分得到(a)所示的结果,第二次划分得到(b)所示的结果。 1 1 1和 3 3 3重叠的部分是 A A A, 2 2 2和 3 3 3重叠的部分是 B B B,因此, 3 3 3作为一个桥梁连接独立的子图 1 1 1和 2 2 2。当然, 4 4 4也作为一个桥梁连接独立的子图 1 1 1和 2 2 2。当然,反过来 1 1 1和 2 2 2也是这个道理。

邻居传播
虽然,执行多次随机划分能提升近邻图的质量。但是,随着随机划分次数的增多,新的随机划分所起的作用越来越小。为了定量描述这一点,我们定义第 m m m次划分所做的贡献为: r m = Σ p ∣ N ~ p m − N ~ p m − 1 ∣ Σ p ∣ N ~ p m ∣ r_m=\frac{\Sigma _p \vert \tilde{N}^m _p - \tilde{N}^{m-1}_{p} \vert}{\Sigma _p \vert \tilde{N}^m _p \vert} rm=Σp∣N~pm∣Σp∣N~pm−N~pm−1∣。然后,假设 q q q是 p p p之前识别的邻居点,而 q q q与 p p p有一个公共真实邻居点 o o o,通过增加随机划分的数量, o o o被识别为 q q q或 p p p的邻居的概率逐渐增加。而无论 o o o被先识别为谁的邻居( q q q或 p p p),另一个点(比如 q q q)可通过该点(比如 p p p)的扩展来识别 o o o。
看图3, o o o被识别为 q q q的邻居(蓝色虚线椭圆内),但它没被识别为 p p p的邻居,因此,我们可以借助 q q q将 o o o识别为 p p p的邻居,此时的邻居传播路径为: p → q → o p \rightarrow q \rightarrow o p→q→o。

具体实施时,对数据集中的每一个点,使用最佳优先的方式来传播邻居。比如点 p p p,我们先访问它的已识别邻居,然后从这些已识别邻居出发执行最佳优先搜索,从而访问更多的点来更新 p p p的邻居。
再具体一点,我们可以把 p p p的已识别邻居加入优先队列,最接近 p p p的点放到队列的顶部,然后,迭代地从队列顶部弹出节点,把该节点的所有未访问邻居加入队列,最后,当队列为空或达到访问点的最大数量时,邻居传播终止。在执行最佳优先搜索的过程中,所有访问点作为 p p p的候选邻居。这一过程的时间成本与 n n n和 d d d成线性关系。
理论分析
为什么多重随机分治和邻居传播效果好,下面给出形式化的分析。
先看第一个引理:
引理1. 假定用一个随机超平面划分数据集,某一点 x i x_i xi和它的真正邻居 x j x_j xj被划分到同一个子集的概率是 P i j P_{ij} Pij。当迭代执行划分 h h h次,相当于使用一个深度为 h h h的树来组织数据集, x i x_i xi与 x j x_j xj被划分到同一个叶子(每个叶子对应一个子集)的概率是 P i j h P_{ij}^h Pijh。当执行上述过程 L L L次(也就是用 L L L棵树分别组织数据), x i x_i xi与 x j x_j xj被划分到同一个叶子的概率是 1 − ( 1 − P i j h ) L 1-(1-P_{ij}^h)^L 1−(1−Pijh)L。
上述过程很容易理解,结果也很容易推导。来看第二个引理:
引理2. x i x_i xi和 x j x_j xj在第 L L L棵随机划分树中被划分到同一叶子,而在前 L − 1 L-1 L−1个随机划分树中都没有划分到同一叶子的概率是 P r L = ( 1 − P i j h ) L − 1 P i j h P_{rL}=(1-P_{ij}^h)^{L-1}P_{ij}^h PrL=(1−Pijh)L−1Pijh。
引理2表明,随着 L L L的增大在第 L L L棵随机划分树中才将 x i x_i xi和 x j x_j xj划分到同一叶子的概率逐渐减小。
引理3. 若 x i x_i xi与 x j x_j xj有同一个邻居点 x n x_n xn,经过 L − 1 L-1 L−1次划分既将 x n x_n xn与 x i x_i xi划分到同一叶子,又将 x n x_n xn与 x j x_j xj划分到同一叶子的概率为 P p L = ( 1 − ( 1 − P i n h ) L − 1 ) ( 1 − ( 1 − P j n h ) L − 1 ) P_{pL}=(1-(1-P_{in}^h)^{L-1})(1-(1-P_{jn}^h)^{L-1}) PpL=(1−(1−Pinh)L−1)(1−(1−Pjnh)L−1),注意 x i x_i xi与 x j x_j xj不一定要划分到同一叶子。
既将 x n x_n xn与 x i x_i xi划分到同一叶子,又将 x n x_n xn与 x j x_j xj划分到同一叶子,这意味着我们可以用 x n x_n xn作为媒介来发现 x i x_i xi与 x j x_j xj之间的邻居关系。而且,随着 L L L的增大上述事件发生的概率也在增大。通过 t t t个媒介点来发现 x i x_i xi与 x j x_j xj之间邻居关系的概率为 P p L = ∏ k = 0 t ( 1 − ( 1 − P n k n k + 1 ) L − 1 ) P_{pL}=\prod _{k=0} ^t (1-(1-P_{n_k n_{k+1}})^{L-1}) PpL=∏k=0t(1−(1−Pnknk+1)L−1),其中 n 0 = i n_0=i n0=i, n t + 1 = j n_{t+1}=j nt+1=j。
下面我们来比较一下经过一个随机划分过程和一个邻居传播过程能够找到真正的邻居关系的概率。假设 x i x_i xi和 x j x_j xj在前 L − 1 L-1 L−1次随机划分中都没有发现他们的邻居关系。
- 不管 L L L为多大,在第 L L L次随机划分中发现他们的邻居关系的概率为 P i j h P_{ij} ^h Pijh
- 通过邻居传播发现他们的邻居关系的概率 P p L P_{pL} PpL随 L L L的增大而增大
- 当 L L L达到某一确定值时,随机划分发现邻居关系的概率 P r L P_{rL} PrL将小于 P p L P_{pL} PpL
上述第3条从 P r L P_{rL} PrL与 P p L P_{pL} PpL的计算表达式中我们可很容易得出, P r L P_{rL} PrL随 L L L为减函数,而 P p L P_{pL} PpL随 L L L为增函数。
当 x i x_i xi与 x j x_j xj有更多相同邻居的时候,邻居传播方案将更具优势。总结一下,我们可以得到如下定理:
定理1. 假定 P = m i n { P i j ∣ ⟨ x i , x j ⟩ ∈ E ( G ) } P=min \lbrace P_{ij} \vert \langle x_i,x_j \rangle \in E(G) \rbrace P=min{Pij∣⟨xi,xj⟩∈E(G)},其中 G G G是精确的近邻图。经过 L L L次随机划分和一阶邻居传播发现 x i x_i xi与 x j x_j xj之间的邻居关系的概率为 1 − ( 1 − P h ) 2 L ( 2 − ( 1 − P h ) L ) 1-(1-P^h)^{2L}(2-(1-P^h)^L) 1−(1−Ph)2L(2−(1−Ph)L),这里假定 x i x_i xi与 x j x_j xj至少有一个公共邻居。
推导: P P P是数据集中发现任意两点邻居关系的概率中最小的那个。经过 L L L次随机划分和一阶邻居传播发现 x i x_i xi与 x j x_j xj之间的邻居关系的概率,其实就是或者经 L L L次随机划分发现 x i x_i xi与 x j x_j xj之间的邻居关系(直接发现邻居关系),或者经过 L L L次随机划分都没有发现 x i x_i xi与 x j x_j xj之间的邻居关系但是将两者的公共邻居( x n x_n xn)都划分到各自的子集(间接发现邻居关系)。前者的概率为 1 − ( 1 − P i j h ) L 1-(1-P_{ij}^h)^L 1−(1−Pijh)L,至少应为 1 − ( 1 − P h ) L 1-(1-P^h)^L 1−(1−Ph)L,后者的概率为 ( 1 − P i j h ) L ⋅ ( 1 − ( 1 − P i n h ) L ) ( 1 − ( 1 − P j n n ) L ) (1-P_{ij}^h)^L \cdot (1-(1-P_{in}^h)^{L})(1-(1-P_{jn}^n)^{L}) (1−Pijh)L⋅(1−(1−Pinh)L)(1−(1−Pjnn)L),至少应为 ( 1 − P h ) L ⋅ ( 1 − ( 1 − P h ) L ) ( 1 − ( 1 − P h ) L ) (1-P^h)^L \cdot (1-(1-P^h)^{L})(1-(1-P^h)^{L}) (1−Ph)L⋅(1−(1−Ph)L)(1−(1−Ph)L)。两者相加即得经过 L L L次随机划分和一阶邻居传播发现 x i x_i xi与 x j x_j xj之间的邻居关系的概率为 1 − ( 1 − P h ) 2 L ( 2 − ( 1 − P h ) L ) 1-(1-P^h)^{2L}(2-(1-P^h)^L) 1−(1−Ph)2L(2−(1−Ph)L)。
时间复杂度
M M M次随机划分的时间复杂度为 O ( M d n log n ) O(Mdn \log {n}) O(Mdnlogn),访问点的最大数量为 T T T时,邻居传播的时间复杂度为 O ( T d n log T ) O(Tdn \log {T}) O(TdnlogT)。前者很容易理解,后者的 T log T T \log {T} TlogT部分我的理解是:执行邻居传播时,访问到的点是以优先队列的形式组织的,而优先队列一般用堆来实现,当访问点的数量为 T T T时维护堆的时间复杂度为 O ( T log T ) O(T \log {T}) O(TlogT)。
在大规模高维场景下, M M M和 T T T都很小,因此总的时间复杂度为 O ( d n log n ) O(dn \log {n}) O(dnlogn)。
算法细节
随机划分
具体实施时,本文采用随机主方向(random principal directions)来执行划分,使得每一个子集的直径足够小。使用随机主方向的原因是已有工作理论证实基于主方向来分层划分点能确保子集的直径快速下降,这样的话,最后在同一子集的点有很大的概率是真正的最近邻。
随机主方向是通过主成分分析(PCA)来获取的。为什么叫做随机主方向呢?原因是计算主方向时,作者并不是根据整个子集中的点计算的,而是从子集中随机取样,根据这些取样计算主方向。主方向是通过Lanczos算法来计算的。
加速
执行多重随机划分或者邻居传播时,一对点之间的距离可能会被计算很多次,为了避免重复计算,作者借助哈希表来存储已经计算过距离的点对。当需要计算一对点之间的距离时,首先通过哈希表检查两者的距离是否已经被计算过,已计算过则取出两者的距离。
添加逆边
当一个点 u u u在另一个点 v v v邻居列表中时,则 v v v也大概率是 u u u的邻居。当选中 u u u作为 v v v的邻居时,立刻添加反向边。
论文的创新点
- 将多重随机划分方案应用到了近邻图的构建上;
- 使用高阶邻居传播提升近邻图的质量;
- 哈希表保存已经计算过距离的点对及距离,适用于有大量重复计算的场景。
注:之前的工作在近邻图构建时,一般选用二阶邻居传播提升近邻图的质量,即改善 p p p的邻居时,将 p p p邻居的邻居作为候选去改善(比如之前介绍的NN-Descent方法),而本文使用最佳优先搜索的方式来改善 p p p的邻居。我的理解是:从 p p p点开始,以 p p p为查询点执行贪婪搜索,返回的最近的几个点作为 p p p的邻居。因此,不仅 p p p的二阶邻居中离 p p p更近的点被考虑,一些高阶邻居中离 p p p更近的点也能被考虑到。
论文的结论
一大波肌肉来袭:

通过多重随机分治和邻居传播两步构建一个适用于大规模数据的近似近邻图。由图4可很清晰看出,本文提出的方法性能远超其它方法。
我的观点或思考
近邻图构建框架: 本文的近邻图构建过程也是满足"First-Coarse-Last-Refinement"框架的,这个框架应该是很多近邻图的构建思路。比如NN-Descent,它的"First-Coarse"部分是随机初试化得到近邻图的过程,它的"Last-Refinement"部分也就是NN-Descent改善邻居的过程。而本文的"First-Coarse"部分是随机分治过程,"Last-Refinement"部分是多重随机分治和邻居传播过程。
邻居传播: 在某点执行选边时,通过最佳优先搜索的方式产生候选集,这类似与插入构图模式。NN-Descent是邻居之间互相了解,这只是一阶邻居,通过最佳优先搜索产生高阶邻居互相了解?
多重随机分治与邻居传播如何协调? 先执行前者再执行后者;边执行前者边执行后者;先执行前者然后边执行前者边执行后者(本文);这是一个需要考虑的问题。