3.3 克拉默法则、体积和线性变换(第三章 行列式)
主要内容
本节讲述了行列式的一些应用。首先是利用克拉默法则去求解线性方程的解,接着,以克拉默法则为基础,引出一种求矩阵的逆的方法。最后讲述了从几何意义上去理解行列式,行列式代表了矩阵围成的平行四边形或平行六面体的面积或体积,并可以通过行列式关联线性变换前后的区域面积或体积。
克拉默法则
为描述方便,首先做一个约定:
对任意 n × n n \times n n×n矩阵 A A A和任意的 R n \mathbb R^n Rn中向量 b \boldsymbol b b,令 A i ( b ) A_i(\boldsymbol b) Ai(b)表示 A A A中第 i i i列由向量 b \boldsymbol b b替换得到的矩阵:
A i ( b ) = [ a 1 ⋯ b ⋯ a n ] A_i(\boldsymbol b) = \begin{bmatrix}\boldsymbol a_1 & \cdots & \boldsymbol b & \cdots & \boldsymbol a_n\end{bmatrix} Ai(b)=[a1⋯b⋯an]
克拉默法则:
设 A A A是一个可逆的矩阵 n × n n \times n n×n矩阵,对 R n \mathbb R^n Rn中任意向量 b \boldsymbol b b,方程 A x = b A\boldsymbol x=\boldsymbol b Ax=b的唯一解可由下式给出:
x i = d e t A i ( b ) d e t A , i = 1 , 2 , ⋯ , n x_i=\frac{det \ A_i(\boldsymbol b)}{det \ A}, i=1,2,\cdots,n xi=det Adet Ai(b),i=1,2,⋯,n
证明:
用 a i \boldsymbol a_i ai表示 A A A的列,用 e i \boldsymbol e_i ei表示单位矩阵 I \boldsymbol I I的列。若 A x = b A\boldsymbol x=\boldsymbol b Ax=b,则由矩阵乘法的定义有:
A I i ( x ) = A [ e 1 ⋯ x ⋯ e n ] = [ A e 1 ⋯ A x ⋯ A e n ] A\boldsymbol I_i(\boldsymbol x) = A\begin{bmatrix}\boldsymbol e_1 & \cdots &\boldsymbol x&\cdots &\boldsymbol e_n\end{bmatrix}=\begin{bmatrix}A\boldsymbol e_1 & \cdots & A\boldsymbol x & \cdots & A\boldsymbol e_n\end{bmatrix} AIi(x)=A[e1⋯x⋯en]=[Ae1⋯Ax⋯Aen]
由于 A e i = a i A\boldsymbol e_i = \boldsymbol a_i Aei=ai,所以,
A I i ( x ) = [ a 1 ⋯ b ⋯ a n ] = A i ( b ) A\boldsymbol I_i(\boldsymbol x)=\begin{bmatrix}\boldsymbol a_1 & \cdots & \boldsymbol b & \cdots &\boldsymbol a_n\end{bmatrix}=A_i(\boldsymbol b) AIi(x)=[a1⋯b⋯an]=Ai(b)
由上节中提到的行列式乘法法则有:
( d e t A ) ( d e t I i ( x ) ) = d e t A i ( b ) (det \ A)(det\ \boldsymbol I_i(\boldsymbol x))=det\ A_i(\boldsymbol b) (det A)(det Ii(x))=det Ai(b)
另一方面,明显的, d e t I i ( x ) = x i det \boldsymbol I_i(\boldsymbol x) = x_i detIi(x)=xi(沿着 I i ( x ) \boldsymbol I_i(\boldsymbol x) Ii(x)的第 i i i行作余因子进行计算就可得到该结论),所以:
( d e t A ) x i = d e t A i ( b ) (det\ A)x_i=det\ A_i(\boldsymbol b) (det A)xi=det Ai(b)
由于 A A A可逆,从而 d e t A ≠ 0 det\ A \neq 0 det A=0,两边同时除去 d e t A det\ A det A,得证。
例:
利用克拉默法则解方程组:
3 x 1 − 2 x 2 = 6 − 5 x 1 + 4 x 2 = 8 \begin{aligned}3x_1-2x_2&=6\\-5x_1+4x_2&=8 \end{aligned} 3x1−2x2−5x1+4x2=6=8
解:
根据上述约定,得知:
A 1 ( b ) = [ 6 − 2 8 4 ] , A 2 ( b ) = [ 3 6 − 5 8 ] A_1(\boldsymbol b)=\begin{bmatrix}6&-2\\8&4\end{bmatrix},A_2(\boldsymbol b)=\begin{bmatrix}3&6\\-5&8\end{bmatrix} A1(b)=[68−24],A2(b)=[3−568]
根据克拉默法则:
x 1 = d e t A 1 ( b ) d e t A = 20 x 2 = d e t A 2 ( b ) d e t A = 27 \begin{aligned}x_1=\frac{det\ A_1(\boldsymbol b)}{det \ A}=20 \\x_2=\frac{det\ A_2(\boldsymbol b)}{det \ A}=27\end{aligned} x1=det Adet A1(b)=20x2=det Adet A2(b)=27
伴随矩阵求矩阵的逆
这里引出一个由克拉默法则求矩阵逆的方法。
考虑一个 n × n n \times n n×n的矩阵 A A A,要求 A A A的逆矩阵 A − 1 A^{-1} A−1。
推导:
显然,如果 A − 1 A^{-1} A−1存在,那么有:
A A − 1 = I AA^{-1} = \boldsymbol I AA−1=I
假设 A − 1 A^{-1} A−1的第 j j j列为 x j \boldsymbol x_j xj,那么有:
A [ x 1 x 2 ⋯ x j ⋯ x n ] = I A\begin{bmatrix}\boldsymbol x_1 & \boldsymbol x_2 & \cdots \boldsymbol x_j & \cdots \boldsymbol x_n\end{bmatrix} = \boldsymbol I A[x1x2⋯xj⋯xn]=I
根据矩阵乘法的定义,有:
[ A x 1 A x 2 ⋯ A x j ⋯ A x n ] = I \begin{bmatrix}A\boldsymbol x_1 & A\boldsymbol x_2 & \cdots A\boldsymbol x_j & \cdots A\boldsymbol x_n\end{bmatrix} = \boldsymbol I [Ax1Ax2⋯Axj⋯Axn]=I
明显的,对于上式左边的第 j j j列,有:
A x j = e j A\boldsymbol x_j = \boldsymbol e_j Axj=ej
根据克拉默法则,对于向量 x j \boldsymbol x_j xj中的第 i i i个元素 x i j x_{ij} xij,有:
x i j = d e t A i ( e j ) d e t A x_{ij} = \frac{det\ A_i(\boldsymbol e_j)}{det\ A} xij=det Adet Ai(ej)
d e t A i ( e j ) det\ A_i(\boldsymbol e_j) det Ai(ej)的意思就是,用 e j \boldsymbol e_j ej去代替矩阵 A A A中的第 i i i列。那么我们按照 A i ( e j ) A_i(\boldsymbol e_j) Ai(ej)的第 i i i列去做余因子展开,有:
d e t A i ( e j ) = ( − 1 ) i + j d e t A j i = C j i det \ A_i(\boldsymbol e_j)=(-1)^{i+j}det\ A{ji} = C_{ji} det Ai(ej)=(−1)i+jdet Aji=Cji
根据上述规律,可以求得 A − 1 A^{-1} A−1的每一个元素,如下式所示:
A − 1 = 1 d e t A [ C 11 C 21 ⋯ C n 1 C 12 C 22 ⋯ C n 2 ⋯ C 1 n C 2 n ⋯ C n n ] A^{-1}=\frac{1}{det\ A}\begin{bmatrix}C_{11} & C_{21}&\cdots&C_{n1}\\C_{12} & C_{22 }& \cdots & C_{n2} \\ \cdots \\C_{1n}&C_{2n}&\cdots &C_{nn}\end{bmatrix} A−1=det A1⎣⎢⎢⎡C11C12⋯C1nC21C22C2n⋯⋯⋯Cn1Cn2Cnn⎦⎥⎥⎤
该余因子矩阵称为 A A A的伴随矩阵,记为 a d j A adj\ A adj A。
行列式和面积/体积
这里仅讨论 R 2 \mathbb R^2 R2和 R 3 \mathbb R^3 R3中的面积和体积问题。
定理:
若 A A A是一个 2 × 2 2\times 2 2×2矩阵,则由 A A A的列确定的平行四边形的面积为 ∣ d e t A ∣ |det\ A| ∣det A∣。若 A A A是一个 3 × 3 3\times 3 3×3矩阵,则由 A A A的列确定的平行六面体的体积为 ∣ d e t A ∣ |det\ A| ∣det A∣。
下面以 R 2 \mathbb R^2 R2为例证明。
证:
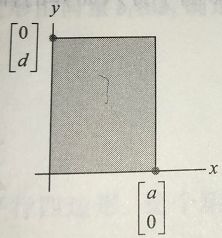
a. 若 A A A为2阶矩阵,定理显然成立。
∣ det [ a 0 0 d ] ∣ = ∣ a d ∣ = a r e a \left |\det\begin{bmatrix}a&0\\0&d\end{bmatrix} \right | = |ad| = area ∣∣∣∣det[a00d]∣∣∣∣=∣ad∣=areab. 对于 A A A不为对角矩阵的情况,基于a的事实,我们只需证明 A = [ a 1 a 2 ] A=\begin{bmatrix}\boldsymbol a_1 & \boldsymbol a_2\end{bmatrix} A=[a1a2]能变换成一个对角矩阵,变换时既不改变相应的平行四边形面积,又不改变 ∣ d e t A ∣ \left | det\ A \right | ∣det A∣。
c. 由上节可以知道,列倍加变换和列交换不会改变行列式的绝对值,而这样的变换足以将矩阵 A A A变换为对角矩阵。
d. 要证明面积的等价性,就要证明矩阵 A A A在通过列倍加变换和列交换变换到对角矩阵的过程中,不会改变列向量构成的平行四边形面积。
d-1. 对于列交换,只是交换两个向量的位置,显然不会改变对应的平行四边形面积。
d-2. 对于列倍加变换,就要证明 a 1 \boldsymbol a_1 a1, a 2 \boldsymbol a_2 a2组成的平行四边形面积,和 a 1 \boldsymbol a_1 a1, a 2 + c a 1 \boldsymbol a_2 + c\boldsymbol a_1 a2+ca1组成的平行四边形的面积相等。这点通过下图可以得知成立( a 2 \boldsymbol a_2 a2和 a 2 + c a 1 \boldsymbol a_2 + c\boldsymbol a_1 a2+ca1到 a 1 \boldsymbol a_1 a1所在的直线 L L L的垂线距离是相等的):
得证。
线性变换
通过行列式,可以把线性变换前后各个点组成的几何图形的面积和体积的关系联系起来。
定理:
设 T : R 2 → R 2 \boldsymbol T: \mathbb R^2 \rightarrow \mathbb R^2 T:R2→R2是一个 2 × 2 2\times 2 2×2矩阵 A A A确定的线性变换,若 S S S是 R 2 \mathbb R^2 R2中一个平行四边形,则:
a r e a o f T ( S ) = ∣ d e t A ∣ ⋅ a r e a o f S area\ of\ \boldsymbol T(S) = \left|det\ A\right|\cdot area\ of\ S area of T(S)=∣det A∣⋅area of S
也就是说, T ( S ) \boldsymbol T(S) T(S)的面积等于 A A A的行列式乘以 S S S的面积。
类似的,若 T \boldsymbol T T是一个由 3 × 3 3 \times 3 3×3矩阵 A A A确定的线性变换,而 S S S是 R 3 \mathbb R^3 R3中的一个平行六面体,则有:
v o l u m e o f T ( S ) = ∣ d e t A ∣ ⋅ v o l u m e o f S volume\ of\ \boldsymbol T(S) = \left|det\ A\right|\cdot volume\ of\ S volume of T(S)=∣det A∣⋅volume of S
证:
仅以 R 2 \mathbb R^2 R2到 R 2 \mathbb R^2 R2的线性变换为例。
假设变换 T \boldsymbol T T对应的矩阵 A = [ a 1 a 2 ] A=\begin{bmatrix}\boldsymbol a_1 & \boldsymbol a_2\end{bmatrix} A=[a1a2]。
考虑 S S S中一个顶点在原点的平行四边形,这个平行四边形由向量 b 1 \boldsymbol b_1 b1和 b 2 \boldsymbol b_2 b2确定,这个平行四边形中的所有点由下列表达式表示:
S = { s 1 b 1 + s 2 b 2 : 0 ≤ s 1 ≤ 1 , 0 ≤ s 2 ≤ 1 } S=\{s_1\boldsymbol b_1 + s_2\boldsymbol b_2:0\leq s_1\leq 1,\ 0\leq s_2 \leq 1\} S={s1b1+s2b2:0≤s1≤1, 0≤s2≤1}
这些点在 T \boldsymbol T T的作用下的像由以下形式的点组成:
T ( s 1 b 1 + s 2 b 2 ) = s 1 T ( b 1 ) + s 2 T ( b 2 ) = s 1 A b 1 + s 2 A b 2 \boldsymbol T(s_1\boldsymbol b_1 + s_2\boldsymbol b_2)=s_1\boldsymbol T(\boldsymbol b_1) + s_2\boldsymbol T(\boldsymbol b_2)=s_1A\boldsymbol b_1 + s_2A\boldsymbol b_2 T(s1b1+s2b2)=s1T(b1)+s2T(b2)=s1Ab1+s2Ab2
由以上表达式可知, T ( S ) \boldsymbol T(S) T(S)是由矩阵 [ A b 1 A b 2 ] \begin{bmatrix}A\boldsymbol b_1 & A\boldsymbol b_2\end{bmatrix} [Ab1Ab2]的列组成的平行四边形,把矩阵 B B B记作 [ b 1 b 2 ] \begin{bmatrix}\boldsymbol b_1 & \boldsymbol b_2\end{bmatrix} [b1b2]。
由本节前面的知识, T ( S ) \boldsymbol T(S) T(S)的面积是 ∣ d e t A B ∣ \left | det\ AB\right | ∣det AB∣,而:
∣ d e t A B ∣ = ∣ d e t A ∣ ⋅ ∣ d e t B ∣ = ∣ d e t A ∣ ⋅ a r e a o f S \left | det\ AB \right | = \left |det\ A \right |\cdot \left | det\ B \right | = \left | det\ A \right | \cdot area\ of\ S ∣det AB∣=∣det A∣⋅∣det B∣=∣det A∣⋅area of S对于顶点不在原点的平行四边形,都可以认为是由顶点在原点的平行四边形平移过去的,因此也满足该定理。
该面积/体积定理还可以推广到任何一种几何形状(利用微积分的思想,化成无数多个小平行四边形的积分)。
例:
若 a a a, b b b是正数,求由方程为 x 1 2 a 2 + x 2 2 b 2 = 1 \frac{x_1^2}{a^2}+\frac{x_2^2}{b^2}=1 a2x12+b2x22=1的椭圆为边界的区域 E E E的面积。
解:
我们可以把 E E E看作单位圆盘 D D D在线性变换 T \boldsymbol T T下的像,这里, T \boldsymbol T T由矩阵 [ a 0 0 b ] \begin{bmatrix}a&0\\0&b\end{bmatrix} [a00b]确定。这是因为若在原空间中有一个向量 u = [ u 1 u 2 ] \boldsymbol u = \begin{bmatrix}u_1\\u_2\end{bmatrix} u=[u1u2],变换后的向量为 x = [ x 1 x 2 ] \boldsymbol x=\begin{bmatrix}x_1\\x_2\end{bmatrix} x=[x1x2],则:
u 1 = x 1 a , u 2 = x 2 b \boldsymbol u_1=\frac{x_1}{a},\ \boldsymbol u_2=\frac{x_2}{b} u1=ax1, u2=bx2
当 u \boldsymbol u u在单位圆盘内时,即满足 u 1 2 + u 2 2 ≤ 1 u_1^2 + u_2^2 \leq 1 u12+u22≤1时, ( x 1 a ) 2 + ( x 2 b ) 2 ≤ 1 (\frac{x_1}{a})^2 + (\frac{x_2}{b})^2 \leq 1 (ax1)2+(bx2)2≤1,所以,变换后的椭圆形内的面积,可以转化成原始空间中圆的面积: ∣ d e t A ∣ ⋅ a r e a o f D = a ⋅ b ⋅ π ( 1 ) 2 = π a b \left | det \ A \right |\cdot area\ of\ D = a\cdot b \cdot \pi(1)^2=\pi ab ∣det A∣⋅area of D=a⋅b⋅π(1)2=πab