4.1 向量空间与子空间
主要内容
本节讲述了向量空间的概念,这里要把之前由几何概念得到的对向量空间的直觉进行进一步抽象和泛化,只要满足定义的一组向量,都可以构成向量空间,例如多项式、实函数等等。在向量空间的基础上,引入了子空间的概念。
向量空间的定义
定义:
一个向量空间是由一些被称为向量的对象构成的非空集合 V V V,在这个集合上定义了两个运算,称为加法和标量乘法,服从以下公理,这些公理必须对 V V V中所有向量 u , v , w \boldsymbol u,\boldsymbol v,\boldsymbol w u,v,w及所有标量 c c c和 d d d均成立。
- u + v \boldsymbol u + \boldsymbol v u+v属于 V V V
- u + v = v + u \boldsymbol u + \boldsymbol v = \boldsymbol v + \boldsymbol u u+v=v+u
- ( u + v ) + w = u + ( v + w ) (\boldsymbol u+ \boldsymbol v) + \boldsymbol w = \boldsymbol u + (\boldsymbol v + \boldsymbol w) (u+v)+w=u+(v+w)
- V V V中存在一个零向量 0 \boldsymbol 0 0,使得 u + 0 = u \boldsymbol u+ \boldsymbol 0 = \boldsymbol u u+0=u
- 对 V V V中每个向量 u \boldsymbol u u,存在 V V V中一个向量 − u -\boldsymbol u −u,使得 u + ( − u ) = 0 \boldsymbol u + (-\boldsymbol u)=\boldsymbol 0 u+(−u)=0
- u \boldsymbol u u与标量 c c c的乘法 c u c\boldsymbol u cu属于 V V V.
- c ( u + v ) = c u + c v c(\boldsymbol u+\boldsymbol v)=c\boldsymbol u + c\boldsymbol v c(u+v)=cu+cv
- ( c + d ) u = c u + d u (c+d)\boldsymbol u=c\boldsymbol u+d\boldsymbol u (c+d)u=cu+du
- c ( d u ) = ( c d ) u c(d\boldsymbol u) = (cd)\boldsymbol u c(du)=(cd)u
- 1 u = u 1\boldsymbol u=\boldsymbol u 1u=u
要证明一个空间 V V V是不是向量空间,就要证明这个空间中的任意一个元素是否满足上述定理。
例:
设 S S S是数的双向无穷序列空间,则其中某一个元素是 { y k } = ( ⋯ , y − 2 , y − 1 , y 0 , y 1 , y 2 , ⋯ ) \{y_k\}=(\cdots,y_{-2},y_{-1},y_0,y_1,y_2,\cdots) {yk}=(⋯,y−2,y−1,y0,y1,y2,⋯),若其中有另一个元素 { z k } \{z_k\} {zk},二者的和由对应各项的和构成, c { y k } c\{y_k\} c{yk}是序列 { c y k } \{cy_k\} {cyk},可以证明 S S S是向量空间。这样的一种集合来自于工程学,当一个信号在离散时间上被测量(采样)时,它就可以被看作是 S S S中的一个元素。我们称 S S S为(离散的)信号空间。
例:
对 n ≥ 0 n \geq 0 n≥0,次数最高为 n n n的多项式集合 P n P_n Pn,由形如下列的多项式组成:
p ( t ) = a 0 + a 1 t + a 2 t 2 + ⋯ + a n t n \boldsymbol p(t)=a_0+a_1t+a_2t^2+\cdots+a_nt^n p(t)=a0+a1t+a2t2+⋯+antn
其系数和变量 t t t均为实数。考虑另一个多项式:
q ( t ) = b 0 + b 1 t + b 2 t 2 + ⋯ + b n t n \boldsymbol q(t)=b_0+b_1t+b_2t^2+\cdots+b_nt^n q(t)=b0+b1t+b2t2+⋯+bntn
二者的和为:
( p + q ) ( t ) = p ( t ) + ( t ) = ( a 0 + b 0 ) + ( a 1 + b 1 ) t + ⋯ + ( a n + b n ) t n (\boldsymbol p + \boldsymbol q)(t)=\boldsymbol p(t)+\boldsymbol (t)=(a_0+b_0)+(a_1+b1)t+\cdots + (a_n+b_n)t^n (p+q)(t)=p(t)+(t)=(a0+b0)+(a1+b1)t+⋯+(an+bn)tn
标量乘法为:
( c p ) ( t ) = c p ( t ) = c a 0 + ( c a 1 ) t + ⋯ + ( c a n ) t n (c\boldsymbol p)(t)=c\boldsymbol p(t)=ca_0+(ca_1)t+\cdots +(ca_n)t^n (cp)(t)=cp(t)=ca0+(ca1)t+⋯+(can)tn
这些定义明显满足公理1和公理6,这是因为 + q \boldsymbol +\boldsymbol q +q和 c p c\boldsymbol p cp均为次数不超过 n n n的多项式。其他公理也可一一证明。于是, P n P_n Pn是一个向量空间。
例:
假设集合 V V V是定义在 D D D上的全体实值函数的集合,则这个集合 V V V也是一个向量空间(省去举例和证明)。这个例子的意义是,将 R n \mathbb R^n Rn中建立的几何直觉上升到一般向量空间。
子空间
在许多问题中,一个向量空间是由一个大的向量空间中适当的向量的子集所构成。在此情形下,向量空间的10个公理中只需要验证三个,其余的自然成立。
定义:
向量空间 V V V的一个子空间是 V V V的一个满足以下三个性质的子集 H H H:
a. V V V中的零向量在 H H H中
b. H H H对向量加法封闭,即对 H H H中任意向量 u , v \boldsymbol u,\boldsymbol v u,v,和 u + v \boldsymbol u+\boldsymbol v u+v仍在 H H H中
c. H H H对标量乘法封闭,即对 H H H中任意向量 u \boldsymbol u u和任意标量 c c c,向量 c u c\boldsymbol u cu仍在 H H H中。
每个子空间都是一个向量空间,反之,每个向量空间是一个子空间(针对本身或其他更大的空间而言)。对两个向量空间,若其中一个在另一个内部,此时子空间这个词被使用,而 V V V的子空间是将 V V V看作更大的子空间。
例:
令 P P P为全体实系数多项式的集合,由于 P P P中运算的定义与函数运算相同,因此, P P P是定义在 R n \mathbb R^n Rn上的全体实值函数的空间一个子空间。另外,对每个 n ≥ 0 n \geq 0 n≥0, P n P_n Pn是 P P P的子空间,这是因为, P n P_n Pn包含零多项式,且 P n P_n Pn中两个多项式之和仍在 P n P_n Pn中,数乘以 P n P_n Pn中一个多项式仍在 P n P_n Pn中。
例:
向量空间 R 2 \mathbb R^2 R2不是 R 3 \mathbb R^3 R3的子空间,因为 R 2 \mathbb R^2 R2甚至不是 R 3 \mathbb R^3 R3的子集。这是因为 R 2 \mathbb R^2 R2中的每个向量含有2个元素,而 R 3 \mathbb R^3 R3中的每个向量则含有3个元素。
另一方面,集合 H = [ s t 0 ] H=\begin{bmatrix}s \\ t \\ 0\end{bmatrix} H=⎣⎡st0⎦⎤, s , t s,t s,t均为实数,是 R 3 \mathbb R^3 R3的一个子集。
例:
R 3 \mathbb R^3 R3中一个不通过原点的平面不是 R 3 \mathbb R^3 R3的子空间,因为此平main不包含 R 3 \mathbb R^3 R3中的零向量。类似的, R 2 \mathbb R^2 R2中一个不通过原点的直线也不是 R 2 \mathbb R^2 R2的子空间。
由一个集合生成的子空间
例:
给定向量空间 V V V中向量 v 1 , v 2 \boldsymbol v_1,\boldsymbol v_2 v1,v2,令 H = S p a n { v 1 , v 2 } H=Span\{\boldsymbol v_1,\boldsymbol v_2\} H=Span{v1,v2},证明 H H H是 V V V的一个子空间
证:
要证明该命题,只需证明对于 H H H中的任意两个向量 u , w \boldsymbol u,\boldsymbol w u,w, c u c\boldsymbol u cu和 u + w \boldsymbol u + \boldsymbol w u+w也在 H H H中。由于 H = S p a n { v 1 , v 2 } H=Span\{\boldsymbol v_1,\boldsymbol v_2\} H=Span{v1,v2},因此有:
u = s 1 v 1 + s 2 v 2 , w = t 1 v 1 + t 2 v 2 \boldsymbol u=s_1\boldsymbol v_1+s_2\boldsymbol v_2,\boldsymbol w=t_1\boldsymbol v_1+t_2\boldsymbol v_2 u=s1v1+s2v2,w=t1v1+t2v2
那么显然有:
u + w = ( s 1 + t 1 ) v 1 + ( s 2 + t 2 ) v 2 \boldsymbol u+\boldsymbol w=(s_1+t_1)\boldsymbol v_1+(s_2+t_2)\boldsymbol v_2 u+w=(s1+t1)v1+(s2+t2)v2
c u = ( c s 1 ) v 1 + ( c s 2 ) v 2 c\boldsymbol u=(cs_1)\boldsymbol v_1+(cs_2)\boldsymbol v_2 cu=(cs1)v1+(cs2)v2
显然, u + w \boldsymbol u+\boldsymbol w u+w和 c u c\boldsymbol u cu都属于 S p a n { v 1 , v 2 } Span\{\boldsymbol v_1,\boldsymbol v_2\} Span{v1,v2},得证。
在后面4.5节中,可以证明 R 3 \mathbb R^3 R3的每一个非零子空间除了 R 3 \mathbb R^3 R3本身,要么是 S p a n { v 1 , v 2 } Span\{\boldsymbol v_1,\boldsymbol v_2\} Span{v1,v2},这里 v 1 , v 2 \boldsymbol v_1,\boldsymbol v_2 v1,v2是两个线性无关的向量,要么是 S p a n { v } , v ≠ 0 Span\{\boldsymbol v\},\boldsymbol v \neq \boldsymbol 0 Span{v},v=0。对第一种情形,此子空间是一个通过原点的平面;对第二种情形,子空间是一条通过原点的直线。
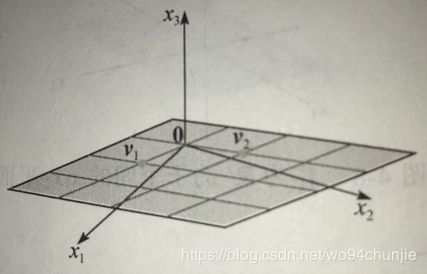
由这个例子,可以推广得到如下的定理:
定理:
若 v 1 , ⋯ , v p \boldsymbol v_1, \cdots, \boldsymbol v_p v1,⋯,vp在向量空间 V V V中,则 S p a n { v 1 , ⋯ , v p } Span\{\boldsymbol v_1,\cdots,\boldsymbol v_p\} Span{v1,⋯,vp}是 V V V的一个子空间。

