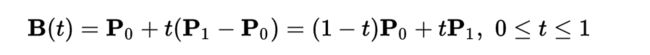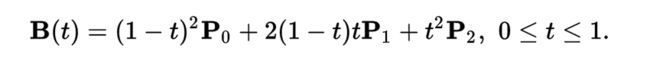Android开发之贝塞尔曲线初体验

什么是贝塞尔曲线，它能够做什么？

贝塞尔曲线的名称来源于一位就职于雷诺的法国工程师Pierre Bézier，他在1962年开始对贝塞尔曲线做了广泛的宣传，他使用这种只需要很少的控制点就能生成复杂平滑曲线的方法来进行汽车车体的工业设计，因为它控制简便却具有极强的描述能力，所以在工业设计和计算机图形学等相关领域得到了广泛应用，比如我们电脑常用的绘图软件PhotoShop里的钢笔工具，这也是贝塞尔曲线的应用之一。

简单点来说，贝塞尔曲线就是能用数学公式将一条曲线很精准的表现出来。

那么在Android开发中，贝塞尔曲线可以帮我们做出什么效果呢？这里举几个例子，简单点的它可以帮助我们做出很自然的平滑动画，比如在一个页面中画出波浪动画，饿了么购物车的商品加入动画等，复杂点的比如QQ消息气泡的拖拽消失等。

关于贝塞尔曲线，我们需要知道什么？

首先我们需要知道这几个词：
数据点：一条路径的起始点和结束点
控制点：决定一条路径的曲线轨迹，根据控制点的个数我们可以把贝塞尔曲线分成一阶、二阶、三阶和多阶贝塞尔曲线。
其中n阶贝塞尔曲线=n-1个控制点，也就是一阶贝塞尔曲线是0个控制点也就是一条直线，二阶贝塞尔曲线是1个控制点，以此类推。
在Android开发中，系统已经帮我们封装好了二阶和三阶的对应实现方法，我们只管调用就行，当然在开发中，我们有时会遇到需要实现多阶贝塞尔曲线的情况，这时我们可以把多阶进行分解，变成多个二阶或者三阶的贝塞尔曲线，再以后的博客里我会再提到，这里先做一个入门的介绍，毕竟不能一口气吃成大胖子。
来看下关于贝塞尔曲线的展示：
一阶贝塞尔曲线：

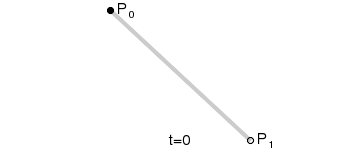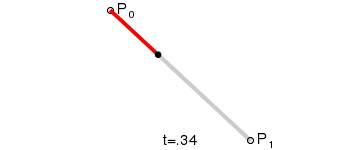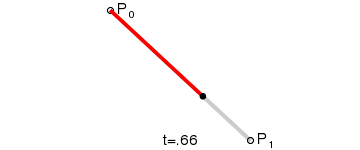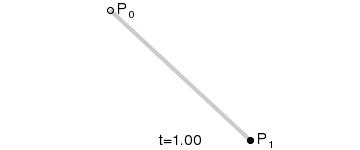
一阶贝塞尔曲线

给定对应的P0和P1，分别是起始点和结束点，对应的表达式：

一阶贝塞尔表达式

二阶贝塞尔曲线：

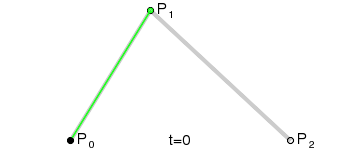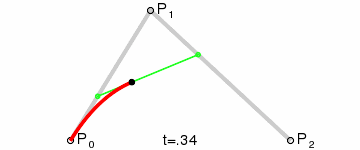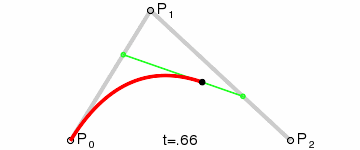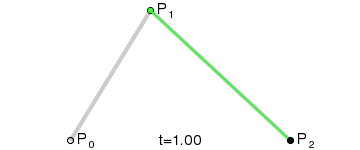
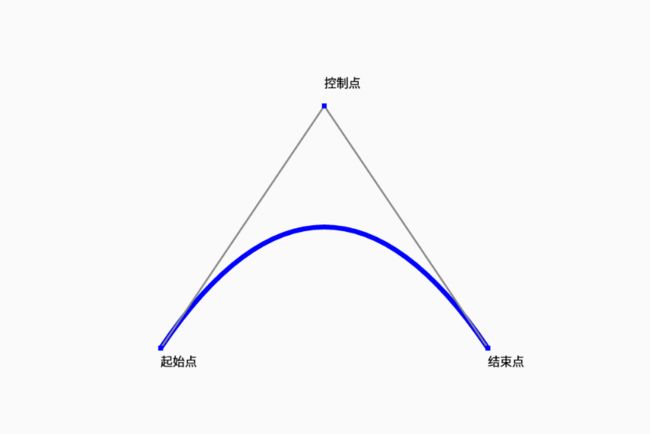
二阶贝塞尔曲线

给定对应的P0和P2，分别是起始点和结束点，P1为控制点，对应的表达式：

二阶贝塞尔表达式

三阶贝塞尔曲线：

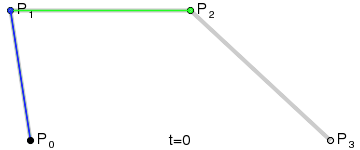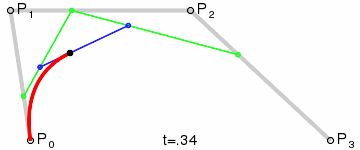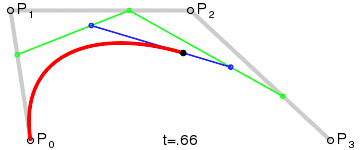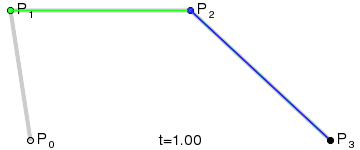
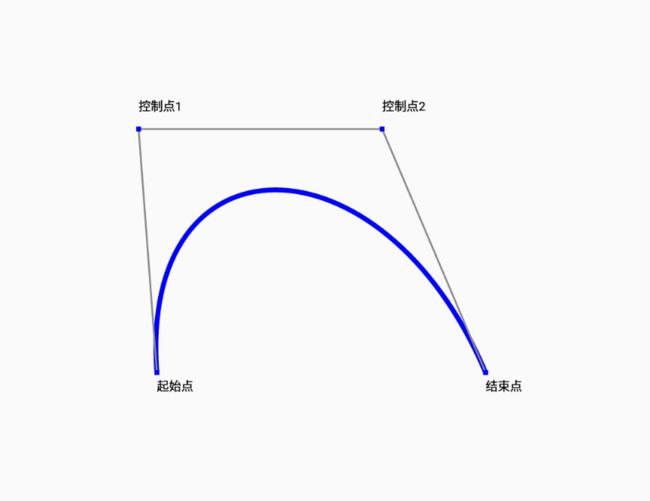
三阶贝塞尔曲线

给定对应的P0和P3，分别是起始点和结束点，P1，P2为控制点，对应的表达式：

三阶贝塞尔表达式

以上的曲线图红色轨迹即为贝塞尔曲线运动轨迹,而绿色的轨迹即为贝塞尔曲线的切线，想了解更多的朋友可以参考下维基百科：贝塞尔曲线
这里有一个贝塞尔曲线的动态演示图，大家玩玩感受一下：贝塞尔曲线的动态演示图

具体代码实现

好了，大概介绍完贝塞尔曲线的概念后，作为开发者，应该手痒痒的想拿去键盘用代码实现一波了吧？
由于一阶贝塞尔曲线没有控制点，就是一条直线，没什么好说的，这里我打算从二阶贝塞尔曲线开始说起，谷歌官方对开发者还是很不错的，已经提前帮我们封装好关于二阶和三阶贝塞尔曲线的实现方法，我们先来看下API：

二阶贝塞尔曲线:
对应的实现方式是：Path.quadTo和Path.rQuadTo，它们分别对应的是绝对坐标和相对坐标，两者是可以互相转换的。

 /**
     * Add a quadratic bezier from the last point, approaching control point
     * (x1,y1), and ending at (x2,y2). If no moveTo() call has been made for
     * this contour, the first point is automatically set to (0,0).
     *
     * @param x1 The x-coordinate of the control point on a quadratic curve
     * @param y1 The y-coordinate of the control point on a quadratic curve
     * @param x2 The x-coordinate of the end point on a quadratic curve
     * @param y2 The y-coordinate of the end point on a quadratic curve
     */
    public void quadTo(float x1, float y1, float x2, float y2) {
        isSimplePath = false;
        native_quadTo(mNativePath, x1, y1, x2, y2);
    }

首先我们先运用Path.moveTo将坐标移动到起始点，然后这里x1，y1代表的是控制点的x，y坐标，x2，y2代表结束点，我们来写个例子：

package com.lcw.view;

import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.util.AttributeSet;
import android.util.DisplayMetrics;
import android.view.MotionEvent;
import android.view.View;
import android.view.WindowManager;

/**
 * 自定义View(二阶贝塞尔曲线)
 * Create by: chenwei.li
 * Date: 2017/4/21
 * Time: 下午11:47
 * Email: [email protected]
 */

public class BezierQuadView extends View {

    //开始点和结束点
    private int mStartXPoint;
    private int mStartYPoint;
    private int mEndXPoint;
    private int mEndYPoint;
    //控制点
    private int mConXPoint;
    private int mConYPoint;

    //路径和画笔
    private Path mPath;
    private Paint mPaint;


    //辅助线画笔,写字画笔
    private Paint mLinePaint;
    private Paint mTextPaint;


    public BezierQuadView(Context context) {
        super(context);
        init(context);
    }


    public BezierQuadView(Context context, AttributeSet attrs) {
        super(context, attrs);
        init(context);
    }

    public BezierQuadView(Context context, AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
        init(context);
    }

    /**
     * 进行初始化的一些操作
     */
    private void init(Context context) {
        //获取屏幕的宽高
        WindowManager windowManager = (WindowManager) context.getSystemService(Context.WINDOW_SERVICE);
        DisplayMetrics displayMetrics = new DisplayMetrics();
        windowManager.getDefaultDisplay().getMetrics(displayMetrics);
        int screenHeight = displayMetrics.heightPixels;
        int screenWidth = displayMetrics.widthPixels;

        //设置各点的位置
        mStartXPoint = screenWidth / 4;
        mStartYPoint = screenHeight / 2;
        mEndXPoint = screenWidth * 3 / 4;
        mEndYPoint = screenHeight / 2;
        mConXPoint = screenWidth / 2;
        mConYPoint = screenHeight / 2 - 400;
        //路径,画笔设置
        mPath = new Path();
        mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
        mPaint.setColor(Color.BLUE);
        mPaint.setStyle(Paint.Style.STROKE);
        mPaint.setStrokeWidth(8);

        //辅助线画笔
        mLinePaint = new Paint(Paint.ANTI_ALIAS_FLAG);
        mLinePaint.setColor(Color.GRAY);
        mLinePaint.setStyle(Paint.Style.STROKE);
        mLinePaint.setStrokeWidth(3);

        //写字画笔
        mTextPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
        mTextPaint.setColor(Color.BLACK);
        mTextPaint.setStyle(Paint.Style.STROKE);
        mTextPaint.setTextSize(20);


    }

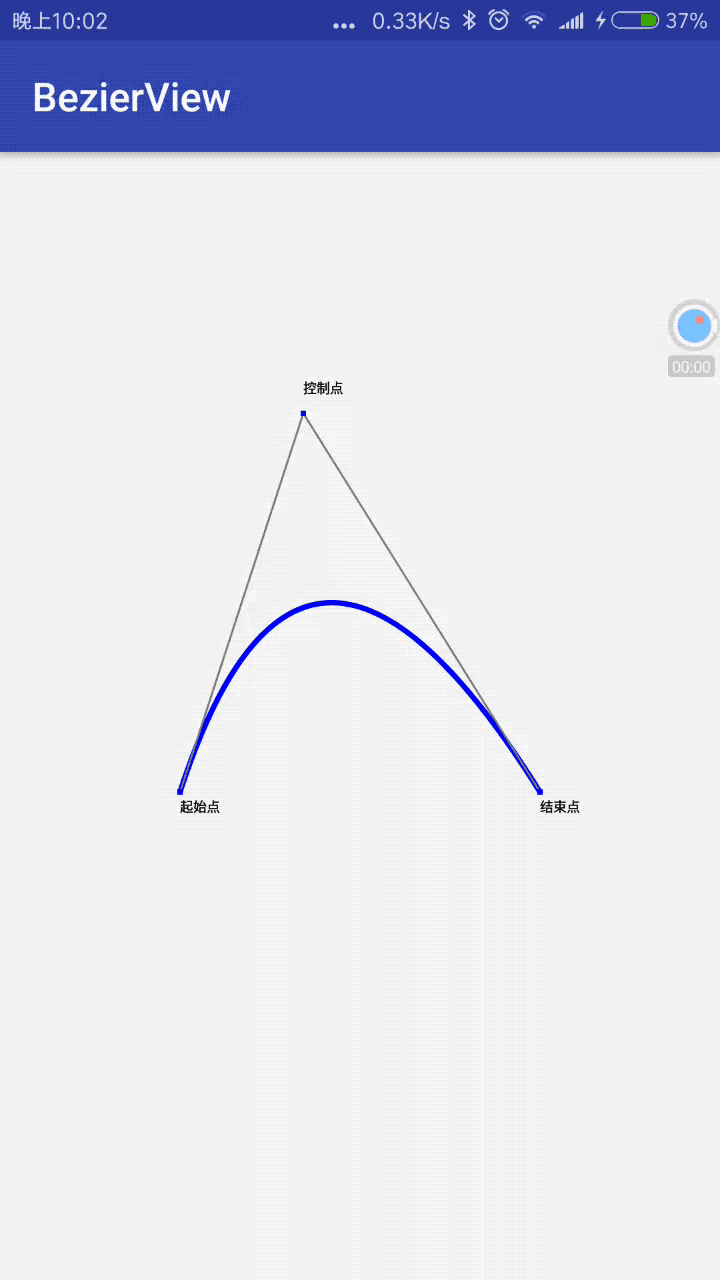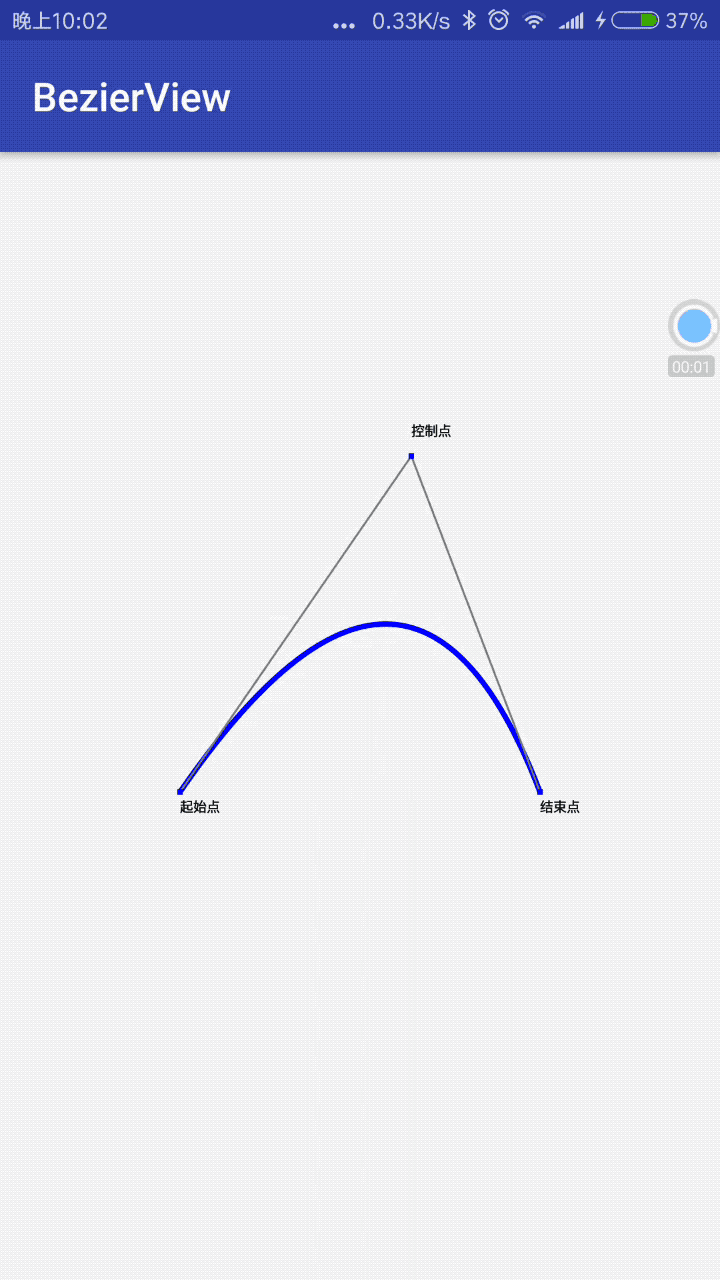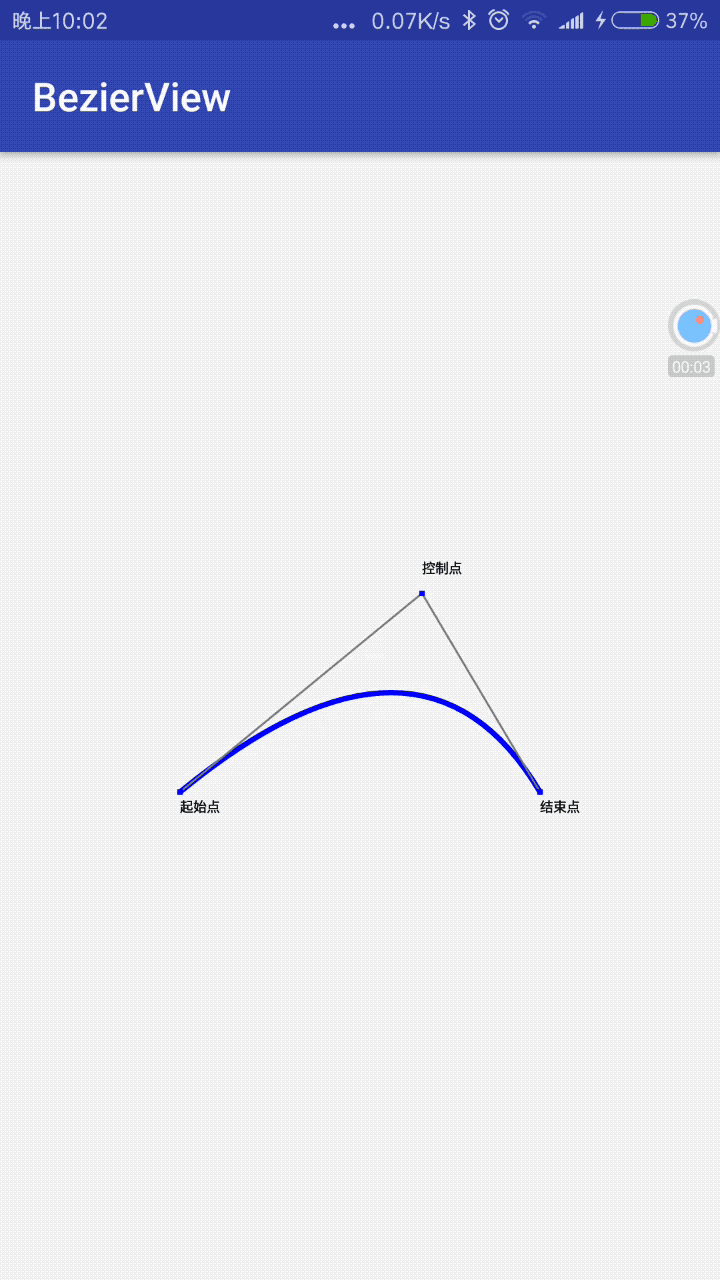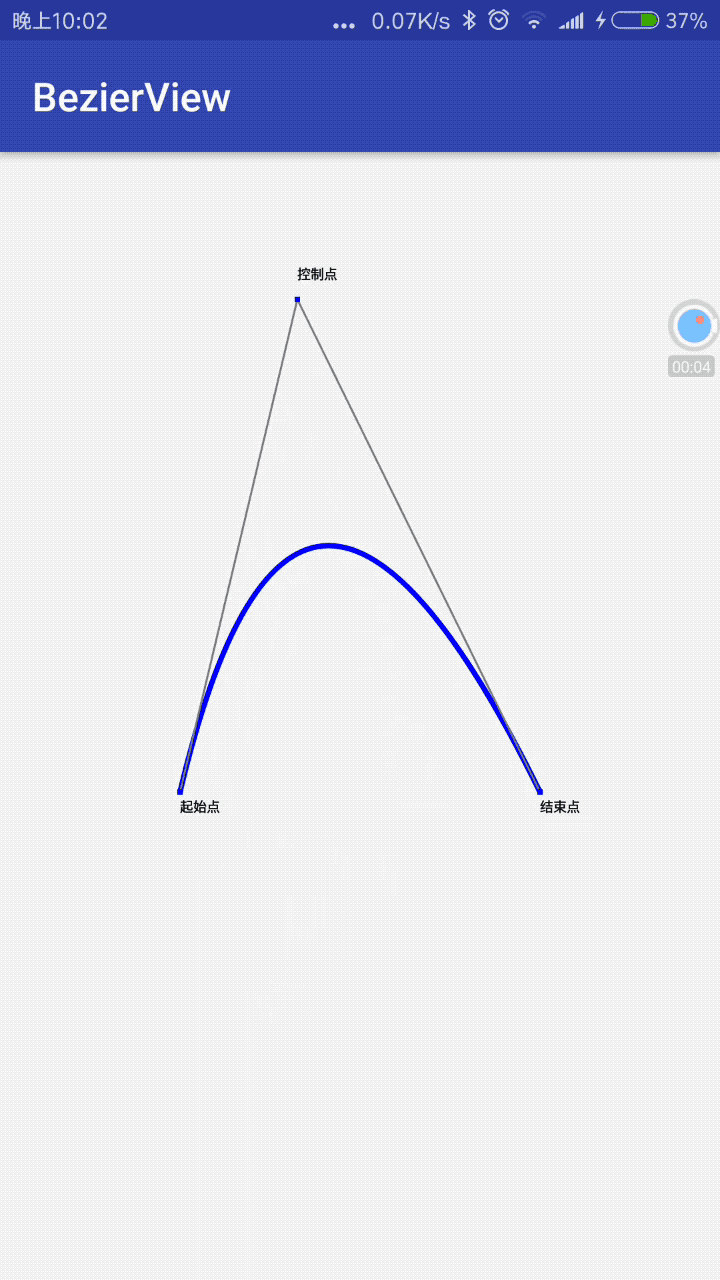
    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        mPath.reset();
        //赛贝尔曲线
        mPath.moveTo(mStartXPoint, mStartYPoint);
        mPath.quadTo(mConXPoint, mConYPoint, mEndXPoint, mEndYPoint);
        canvas.drawPath(mPath, mPaint);

        //辅助线
        canvas.drawLine(mStartXPoint, mStartYPoint, mConXPoint, mConYPoint, mLinePaint);
        canvas.drawLine(mConXPoint, mConYPoint, mEndXPoint, mEndYPoint, mLinePaint);

        //文字
        canvas.drawPoint(mStartXPoint, mStartYPoint, mPaint);
        canvas.drawText("起始点", mStartXPoint, mStartYPoint + 30, mTextPaint);
        canvas.drawPoint(mEndXPoint, mEndYPoint, mPaint);
        canvas.drawText("结束点", mEndXPoint, mEndYPoint + 30, mTextPaint);
        canvas.drawPoint(mConXPoint, mConYPoint, mPaint);
        canvas.drawText("控制点", mConXPoint, mConYPoint - 30, mTextPaint);

    }

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        switch (event.getAction()){
            case MotionEvent.ACTION_MOVE:
                mConXPoint= (int) event.getX();
                mConYPoint=(int)event.getY();
                invalidate();
                break;
        }
        return true;
    }
}

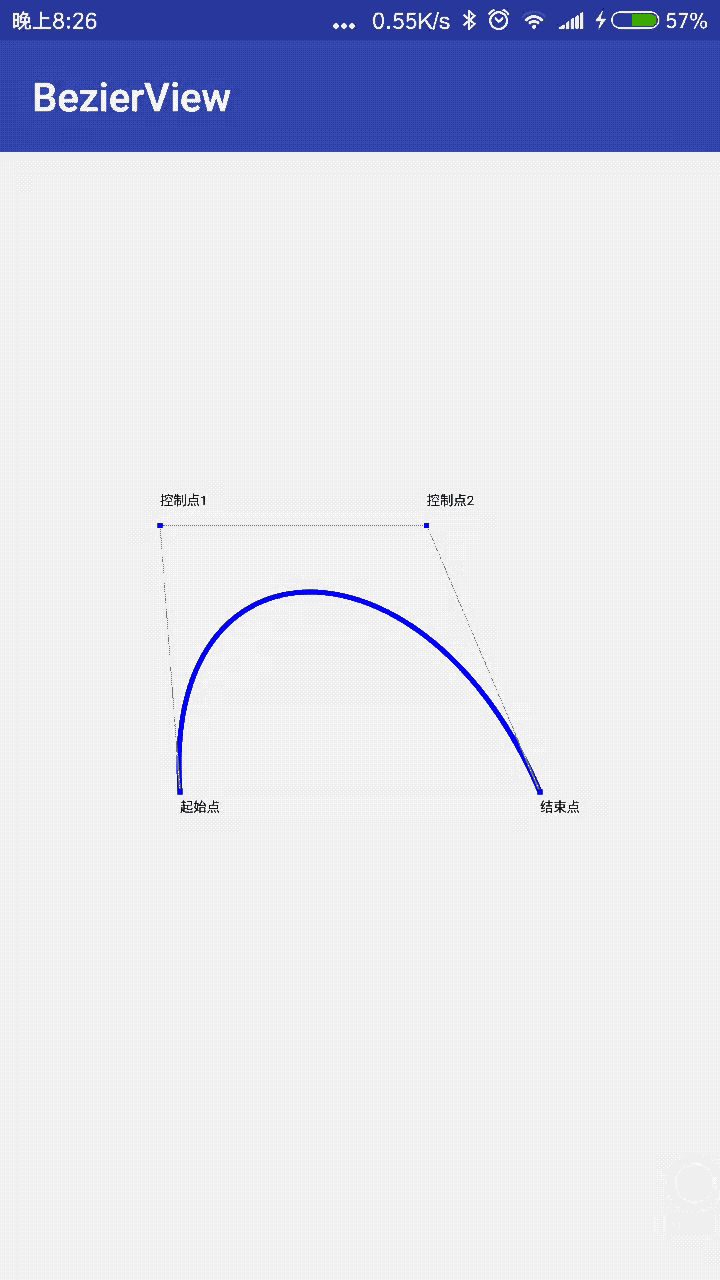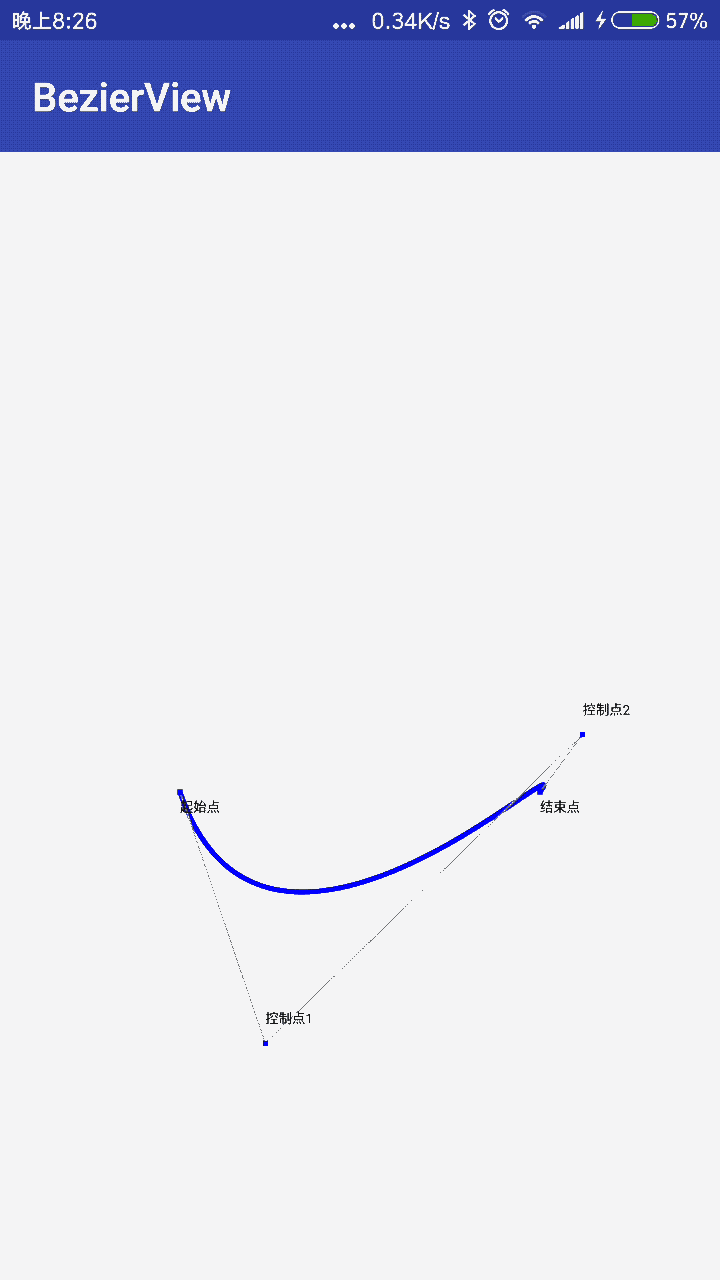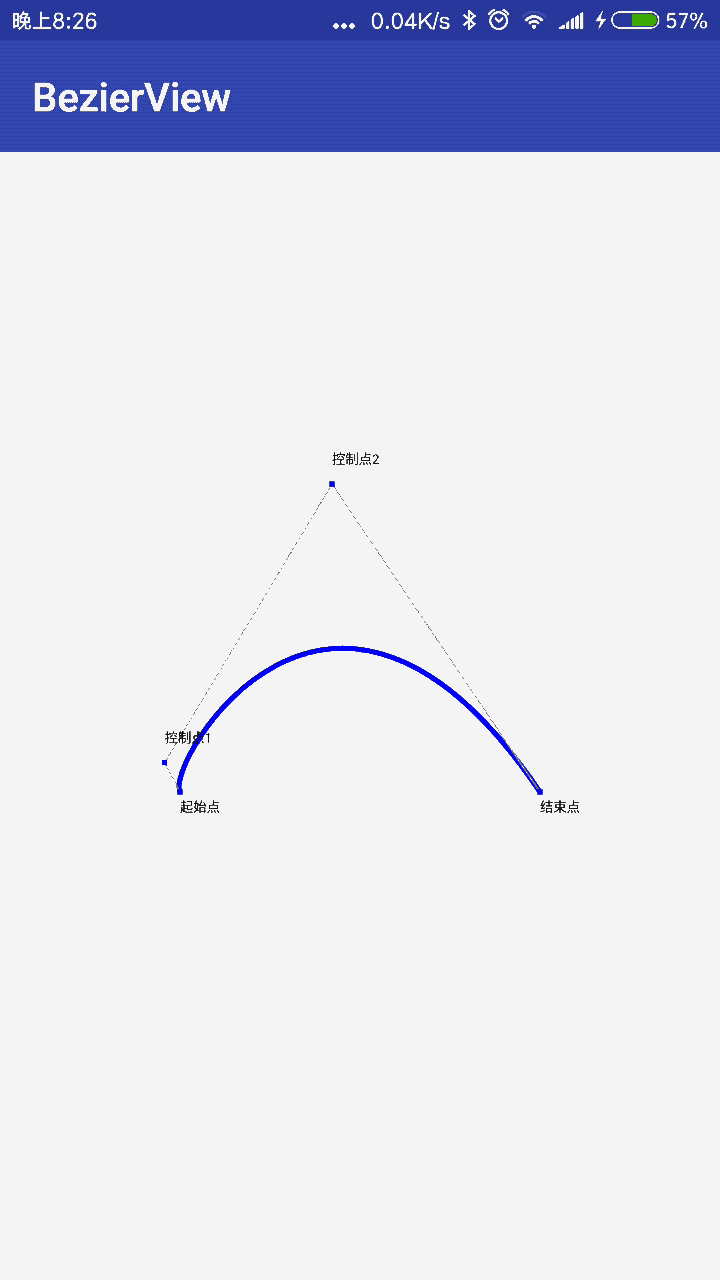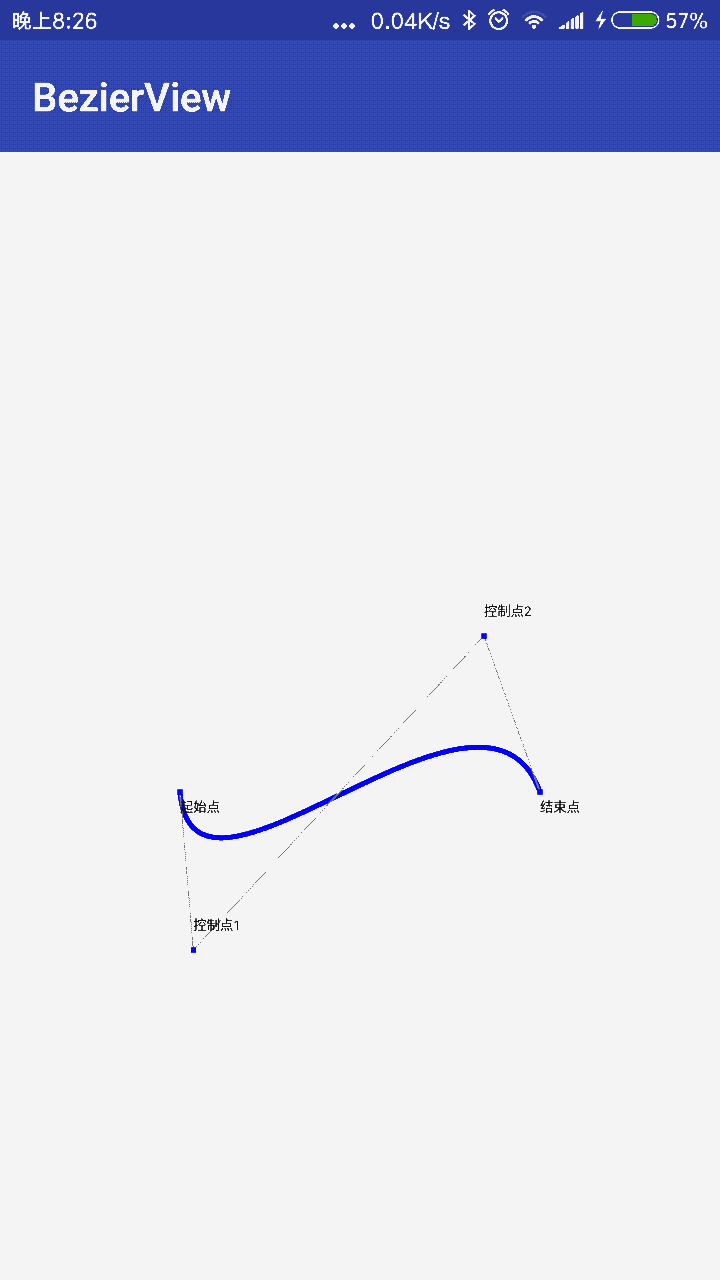
三阶贝塞尔曲线:
对应的实现方式是：Path.cubicTo和Path.rCubicTo，它们分别对应的是绝对坐标和相对坐标，两者是可以互相转换的。

    /**
     * Add a cubic bezier from the last point, approaching control points
     * (x1,y1) and (x2,y2), and ending at (x3,y3). If no moveTo() call has been
     * made for this contour, the first point is automatically set to (0,0).
     *
     * @param x1 The x-coordinate of the 1st control point on a cubic curve
     * @param y1 The y-coordinate of the 1st control point on a cubic curve
     * @param x2 The x-coordinate of the 2nd control point on a cubic curve
     * @param y2 The y-coordinate of the 2nd control point on a cubic curve
     * @param x3 The x-coordinate of the end point on a cubic curve
     * @param y3 The y-coordinate of the end point on a cubic curve
     */
    public void cubicTo(float x1, float y1, float x2, float y2,
                        float x3, float y3) {
        isSimplePath = false;
        native_cubicTo(mNativePath, x1, y1, x2, y2, x3, y3);
    }

来看下运行效果图：

二阶贝塞尔曲线.png

首先我们先运用Path.moveTo将坐标移动到起始点，然后这里x1，y1代表的是控制点1的x，y坐标，x2，y2代表的是控制点2的x，y坐标，x3，y3代表结束点，我们来写个例子：

package com.lcw.view;

import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.util.AttributeSet;
import android.util.DisplayMetrics;
import android.view.View;
import android.view.WindowManager;

/**
 * 自定义View(三阶贝塞尔曲线)
 * Create by: chenwei.li
 * Date: 2017/4/21
 * Time: 下午11:47
 * Email: [email protected]
 */

public class BezierCubicView extends View {

    //开始点和结束点
    private int mStartXPoint;
    private int mStartYPoint;
    private int mEndXPoint;
    private int mEndYPoint;
    //控制点
    private int mConOneXPoint;
    private int mConOneYPoint;
    private int mConTwoXPoint;
    private int mConTwoYPoint;

    //路径和画笔
    private Path mPath;
    private Paint mPaint;


    //辅助线画笔,写字画笔
    private Paint mLinePaint;
    private Paint mTextPaint;


    public BezierCubicView(Context context) {
        super(context);
        init(context);
    }


    public BezierCubicView(Context context, AttributeSet attrs) {
        super(context, attrs);
        init(context);
    }

    public BezierCubicView(Context context, AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
        init(context);
    }

    /**
     * 进行初始化的一些操作
     */
    private void init(Context context) {
        //获取屏幕的宽高
        WindowManager windowManager = (WindowManager) context.getSystemService(Context.WINDOW_SERVICE);
        DisplayMetrics displayMetrics = new DisplayMetrics();
        windowManager.getDefaultDisplay().getMetrics(displayMetrics);
        int screenHeight = displayMetrics.heightPixels;
        int screenWidth = displayMetrics.widthPixels;

        //设置各点的位置
        mStartXPoint = screenWidth / 4;
        mStartYPoint = screenHeight / 2;
        mEndXPoint = screenWidth * 3 / 4;
        mEndYPoint = screenHeight / 2;
        mConOneXPoint = screenWidth / 2 - 300;
        mConOneYPoint = screenHeight / 2 - 400;
        mConTwoXPoint = screenWidth / 2 + 100;
        mConTwoYPoint = screenHeight / 2 - 400;
        //路径,画笔设置
        mPath = new Path();
        mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
        mPaint.setColor(Color.BLUE);
        mPaint.setStyle(Paint.Style.STROKE);
        mPaint.setStrokeWidth(8);

        //辅助线画笔
        mLinePaint = new Paint(Paint.ANTI_ALIAS_FLAG);
        mLinePaint.setColor(Color.GRAY);
        mLinePaint.setStyle(Paint.Style.STROKE);
        mLinePaint.setStrokeWidth(3);

        //写字画笔
        mTextPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
        mTextPaint.setColor(Color.BLACK);
        mTextPaint.setStyle(Paint.Style.STROKE);
        mTextPaint.setTextSize(20);


    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        //赛贝尔曲线
        mPath.moveTo(mStartXPoint, mStartYPoint);
        mPath.cubicTo(mConOneXPoint, mConOneYPoint,mConTwoXPoint,mConTwoYPoint,mEndXPoint, mEndYPoint);
        canvas.drawPath(mPath, mPaint);

        //辅助线
        canvas.drawLine(mStartXPoint, mStartYPoint, mConOneXPoint, mConOneYPoint, mLinePaint);
        canvas.drawLine(mConOneXPoint, mConOneYPoint, mConTwoXPoint, mConTwoYPoint, mLinePaint);
        canvas.drawLine(mConTwoXPoint, mConTwoYPoint, mEndXPoint, mEndYPoint, mLinePaint);

        //文字
        canvas.drawPoint(mStartXPoint, mStartYPoint, mPaint);
        canvas.drawText("起始点", mStartXPoint, mStartYPoint + 30, mTextPaint);
        canvas.drawPoint(mEndXPoint, mEndYPoint, mPaint);
        canvas.drawText("结束点", mEndXPoint, mEndYPoint + 30, mTextPaint);
        canvas.drawPoint(mConOneXPoint, mConOneYPoint, mPaint);
        canvas.drawText("控制点1", mConOneXPoint, mConOneYPoint - 30, mTextPaint);
        canvas.drawPoint(mConTwoXPoint, mConTwoYPoint, mPaint);
        canvas.drawText("控制点2", mConTwoXPoint, mConTwoYPoint - 30, mTextPaint);


    }
}

来看下运行效果图：

三阶贝塞尔曲线.png

现在，我们监听下屏幕的触摸事件，让控制点随着我们手指的移动而移动，看看会是什么样的效果：

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        switch (event.getAction()){
            case MotionEvent.ACTION_MOVE:
                mConXPoint= (int) event.getX();
                mConYPoint=(int)event.getY();
                invalidate();
                break;
        }
        return true;
    }

二阶贝塞尔曲线演示

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        switch (event.getAction() & MotionEvent.ACTION_MASK) {
            case MotionEvent.ACTION_POINTER_DOWN:
                mFlag = true;
                break;
            case MotionEvent.ACTION_POINTER_UP:
                mFlag = false;
                break;
            case MotionEvent.ACTION_MOVE:
                mConOneXPoint = (int) event.getX(0);
                mConOneYPoint = (int) event.getY(0);
                if (mFlag) {
                    mConTwoXPoint = (int) event.getY(1);
                    mConTwoYPoint = (int) event.getY(1);
                }
                invalidate();
                break;
        }
        return true;
    }

三阶贝塞尔曲线演示

怎么样，曲线的绘制很自然吧，这就是贝塞尔曲线的入门使用了。入门篇到这里就结束了，下次给朋友们带来贝塞尔曲线的进阶篇。

源码下载:

这里附上源码地址（欢迎Star，欢迎Fork）：源码下载

Android开发之贝塞尔曲线初体验

什么是贝塞尔曲线，它能够做什么？

关于贝塞尔曲线，我们需要知道什么？

具体代码实现

源码下载:

你可能感兴趣的:(Android开发之贝塞尔曲线初体验)