【集体智慧编程】第二章、提供推荐
一、前言
本章即将告诉大家,如何根据群体偏好来为人们提供推荐。有许多针对于此的应用,如:在线购物中的商品推荐、热门网站的推荐,以及帮助人们寻找音乐和影片的应用。本章将告诉你如何构筑一个系统,用以寻找具有相同品味的人,并根据他人的喜好自动给出推荐。
也许在使用如Amazon这样的在线购物网站之前,你已经接触过某些推荐类引擎了。Amazon会对所有购物者的购买习惯进行追踪,并在你登陆网站时,利用这些信息将你可能会喜欢的商品推荐给你。Amazon甚至还能够向你推荐你可能会喜欢的影片,即便你此前也许只从该网站购买过书籍。还有一些在线的音乐会售票代理站点,它们会查看你以前观看演出的历史,并提醒你即将到来的演出,说不定这些演出是值得一看的。又比如像reddit.com这样的站点,它会让你对其他Web站点的链接进行投票,然后利用投票结果推荐你也许会感兴趣的其他链接。
从这些例子中,你可以看到,我们能够使用许多不同的方式来搜集兴趣偏好。有时候,这些数据可能来自于人们购买的物品,以及有关这些物品的评价信息,这些评论可能会被表达成“是/否”之类的投票表决,或者是从1到5的评价值,本章中,我们将对这些形色各异的表达方法进行考查,以便能够利用同一组算法对其进行处理,同时还讲建立几个涉及电影评分和社会化书签的可运行的例子。
二、协作型过滤
我们知道,要想了解商品、影片或娱乐性网站的推荐信息,最没有技术含量的方法莫过于向朋友们询问,我们也知道,这其中有一部分人的品味会比其他人的高一些。通过观察这些人是否通常也和我们一样喜欢同样的东西,可以逐渐对这些情况有所了解。不过随着选择越来越多,要想通过询问一小群人来确定我们想要的东西,将会变得越来越不切实际,因为他们可能并不了解所有的选择。这就是为什么人们要发展出一套被称为协作型过滤的技术。
一个协作型过滤算法通常的做法是对一大群人进行搜索,并从中找出与我们品味相近的一小群人。算法会对这些人所偏爱的其他内容进行考查,并将它们组合起来构造出一个经过排名的推荐列表。有许多不同的方法可以帮助我们确定哪些人与自己的品味相近,并将他们的选择组合成列表。
科普:
术语“协作型过滤”是David Goldberg 1992年在施乐帕克研究中心(Xerox PARC)的一篇题为《Using collaborative filtering to weave an information tapestry》的论文中首次使用的。他设计了一个名叫Tapestry的系统,该系统允许人们根据自己对文档感兴趣的程度为其添加标注,并利用这一信息为他人进行文档过滤。
(1)搜集偏好
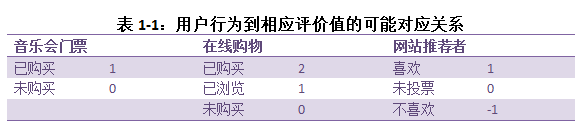
不管偏好是如何表达的,我们需要一种方法来将它们对应到数字。加入我们正在架设一个购物网站,不妨用数字1来代表有人过去曾购买过某件商品,用数字0表示未曾购买过任何商品。而对于一个新闻故事的投票网站,我们可以分别用数字-1,0和1来表达“不喜欢”、“没有投票”、“喜欢”,如下表所示:
(2)寻找相近的用户
搜集完人们的偏好数据之后,我们需要有一种方法来确定人们在品味方面的相似程度。为此,我们可以将每个人与所有其他人进行对比,并计算他们的相似度评价值。这里将介绍两套计算相似度评价值的体系
1. 欧几里德距离
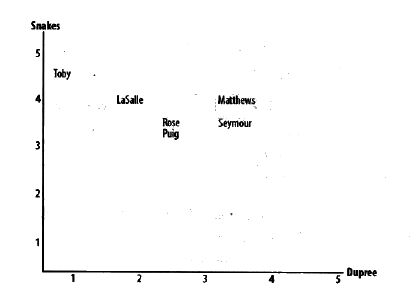
计算相似度评价值的一个非常简单的方法是使用欧几里德距离评价方法。它以经过人们一致评价的物品为坐标轴,然后将参与评价的人绘制到图上,并考查他们彼此间的距离远近。如下图所示:
该图显示了处于“偏好空间”中人们的分布状况。Toby和Snakes轴线和Dupree轴线上所标示的数值分别是4.5和1.0。两人在“偏好空间”中的距离越近,他们的兴趣偏好就越相似。因为这张图是二维的,所以在同一时间内你只能看到两项评分,但是这一规则对于更多数量的评分项而言也是同样适用的。
>>from math import sqrt
>>sqrt(pow(4.5-4.2)+pow(1-2,2))
1.1180339887498949为了计算图上Toby和LaSalle之间的距离,我们可以计算出每一轴向上的差值,求平方后再相加,最后对总和取平方根。偏好越相似的人,其距离就越短。我们还需要一个函数,来对偏好越相近的情况给出越大的值。为此,我们可以将函数值加1(这样就可以避免遇到被零整除的错误了),并取其倒数。
>>1/(1+sqrt(pow(4.5-4.2)+pow(1-2,2)))
0.47213595499957939这一新的函数总是返回介于0到1之间的值,返回1则表示两人具有一样的偏好。我们将前述知识结合起来,就可以构造出用来计算相似度的函数了。
from math import sqrt
# 返回一个有关person1与person2的基于距离的相似度评价
def sim_distance(prefs, person1, person2):
# 得到shared_items的列表
si={}
for item in prefs[person1]:
if item in prefs[person2]:
si[item]=1
# 如果两者没有共同之处,则返回0
if len(si)==0: return 0
# 计算所有差值的平方和
sum_of_squares = sum([pow(prefs[person1][item]-prefs[person2][item], 2)
for item in prefs[person1] if item in prefs[person2]])
return 1/(1+sqrt(sum_of_squares))我们可以调用该函数,分别传入两个人的名字,并计算出相似度的评价值。
2. 皮尔逊相关度
除了欧几里德距离,还有一种更复杂一些的方法可以用来判断人们兴趣的相似度,那就是皮尔逊相关系数。该相关系数是判断两组数据与某一直线拟合程度的一种度量。对应的公式比欧几里德距离评价的计算公式更复杂,但是它在数据不是很规范的时候(比如,影评者对影片的评价总是相对于平均水平偏离很大时),会倾向于给出更好的结果。
为了形象地展现这一方法,我们可以在图上标示出两位评论者的评分情况,如下图所示。Mick LaSalle为《Superman》评了3分,而Gene Seymour则评了5分,所以该影片被定位在图中的(3,5)处。
在图上,我们还可以看到一条直线。因其绘制原则是尽可能地靠近图上的所有坐标点,故而被称为最佳拟合线。如果两位评论者对所有影片的评分情况都相同,那么这条直线将成为对角线,并且会与图上所有的坐标点都相交,从而得到一个结果为1的理想相关度评价。对于如上图所示的情况,由于评论者对部分影片的评分不尽相同,因而相关系数大约为0.4左右。
在采用皮尔逊方法进行评价时,我们可以从图上发现一个值得注意的地方,那就是它修正了“夸大分值”的情况。在这张图中,虽然Jack Matthews总是倾向于给出比Lisa Rose更高的分值,但最终的直线仍然是拟合的,这是因为他们两者有着相对近似的偏好。如果某人总是倾向于给出比另一个人更高的分值,而二者的分值之差又始终保持一致,则他们依然总是倾向于给出比另一个人更高的分值,而二者的分值之差又始终保持一致,则他们依然可能会存在很好的相关性。此前提到过的欧几里德距离评价方法,会因为一个人的评价始终比另一个人的更为“严格”(从而导致评价始终相对偏低),而得出两者不相近的结论,即使他们的品味很相似也是如此。而这一行为是否就是我们想要的结果,则取决于具体的应用场景。
皮尔逊相关度评价算法首先会找出两位评论者都曾评价过的物品,然后计算两者的评分总和与平方和,并求得评分的乘积之和。最后,算法利用这些计算结果计算出皮尔逊相关系数。不同于距离度量法,这一公式不是非常的直观,但是通过除以将所有变量的变化值相乘后得到的结果,它的确能够告诉我们变量的总体变化情况。
# 返回p1和p2的皮尔逊相关系数
def sim_pearson(prefs, p1, p2):
# 得到双方都曾评价过的物品列表
si = {}
for item in prefs[p1]:
if item in prefs[p2]: si[item]=1
# 得到列表元素的个数
n = len(si)
# 如果两者没有共同之处,则返回1
if n==0: return 1
# 对所有偏好求和
sum1 = sum([prefs[p1][it] for it in si])
sum2 = sum([prefs[p2][it] for it in si])
# 求平方和
sum1Sq = sum([pow(prefs[p1][it], 2) for it in si])
sum2Sq = sum([pow(prefs[p2][it], 2) for it in si])
# 求乘积之和
pSum = sum([prefs[p1][it] * prefs[p2][it] for it in si])
# 计算皮尔逊评价值
num = pSum-(sum1*sum2/n)
den = sqrt((sum1Sq-pow(sum1, 2)/n) * (sum2Sq-pow(sum2, 2)/n))
if den == 0: return 0
r = num/den
return r(3)数据集来源:http://grouplens.org/datasets/movielens/
这里我下载了2016年1月更新的ml-latest-small.zip用来做实验
def loadMovieLens():
# 获取影片标题
movies = {}
xlrd.Book.encoding = "utf-8"
data1 = xlrd.open_workbook('movies.xlsx')
table1 = data1.sheets()[0] # 第1个sheet
nrows1 = table1.nrows # 行数
ncols1 = table1.ncols # 列数
for rownum in range(1, nrows1):
row1 = table1.row_values(rownum) # row是一行的数据
if row1:
movies[row1[0]] = row1[1]
# 加载数据
prefs={}
data2 = xlrd.open_workbook('ratings.xlsx')
table2 = data2.sheets()[0] # 第1个sheet
nrows2 = table2.nrows # 行数
ncols2 = table2.ncols # 列数
for rownum in range(1, nrows2):
row2 = table2.row_values(rownum)
if row2:
prefs.setdefault(row2[0], {})
prefs[row2[0]][movies[row2[1]]] = float(row2[2])
return prefs解压后得到的是csv文件,转化为xlsx后将数据取出来转化为字典的形式存起来。
# getRecommendations函数会循环遍历所有字典prefs中的其他人。
# 针对每一次循环,它会计算由person参数所指定的人员与这些人的相似度。
# 然后它会循环遍历所有打过分的项。
# 每一项的最终评论值的计算方法--用每一项的评价值乘以相似度,并将所得乘积累加起来。
# 最后,我们将每个总计值除以相似度之和,借此对评价值进行归一化处理,然后返回一个经过排序的结果
# 利用所有他人评价值的加权平均,为某人提供建议
def getRecommendations(prefs, person, similarity=sim_pearson):
totals = {}
simSums = {}
for other in prefs:
# 不要和自己做比较
if other == person: continue
sim = similarity(prefs, person, other)
# 忽略评价值为零或小于零的情况
if sim <= 0: continue
for item in prefs[other]:
# 只对自己还未曾看过的影片进行评价
if item not in prefs[person] or prefs[person][item] == 0:
# 相似度*评价值
totals.setdefault(item, 0)
totals[item] += prefs[other][item]*sim
# 相似度之和
simSums.setdefault(item, 0)
simSums[item] += sim
# 建立一个归一化的列表
rankings = [(total/simSums[item], item) for item, total in totals.items()]
# 返回经过排序的列表
rankings.sort()
rankings.reverse()
return rankings获取基于用户的推荐
prefs = loadMovieLens()
print getRecommendations(prefs, 87)[0:30]输出如下:
[(5.000000000000001, u"Mummy's Hand, The (1940)"), (5.0, u'Young at Heart (a.k.a. Young@Heart) (2007)'), (5.0, u'Women on the 6th Floor, The (Les Femmes du 6\u732bme \u8121tage) (2010)'), (5.0, u'Werckmeister Harmonies (Werckmeister harm\u8d38ni\u8c29k) (2000)'), (5.0, u'War Photographer (2001)'), (5.0, u"Waiting for 'Superman' (2010)"), (5.0, u'Traviata, La (1982)'), (5.0, u'Topkapi (1964)'), (5.0, u'Time of the Gypsies (Dom za vesanje) (1989)'), (5.0, u'Three Ages (1923)'), (5.0, u'This Is My Father (1998)'), (5.0, u'The Liberator (2013)'), (5.0, u'The Hateful Eight (2015)'), (5.0, u'Temptress, The (1926)'), (5.0, u'Syrup (2013)'), (5.0, u'Symbol (Shinboru) (2009)'), (5.0, u'Swan, The (1956)'), (5.0, u'Svengali (1931)'), (5.0, u'Superman/Batman: Public Enemies (2009)'), (5.0, u'Strawberry and Chocolate (Fresa y chocolate) (1993)'), (5.0, u'Stonewall (1995)'), (5.0, u'Star Wreck: In the Pirkinning (2005)'), (5.0, u"Star Maker, The (Uomo delle stelle, L') (1995)"), (5.0, u'Speedy (1928)'), (5.0, u'Sleepwalk with Me (2012)'), (5.0, u'Six-String Samurai (1998)'), (5.0, u'Sherlock Holmes and the Voice of Terror (1942)'), (5.0, u'Sherlock Holmes Faces Death (1943)'), (5.0, u"Shackleton's Antarctic Adventure (2001)"), (5.0, u'School For Scoundrels (1960)')]