关于K-fold cross validation 下不同的K的选择的疑惑？

 在K-fold cross validation 下 比较不同的K的选择对于参数选择（模型参数，CV意义下的估计的泛化误差）以及实际泛化误差的影响。更一般的问题，在实际模型选择问题中，选择几重交叉验证比较合适？

 

交叉验证的背景知识：

CV是用来验证模型假设（hypothesis）性能的一种统计分析方法，基本思想是在某种意义下将原始数据进行分组，一部分作为训练集，一部分作为验证集，使用训练集对每个hypothesis进行训练，再用验证集对每个hypothesis的性能进行评估，然后选取性能最好的hypothesis作为问题对应的模型。

 

常用CV 方法：

1. Hold-out method

最简单的验证方法，将训练数据随机分为两份（典型做法是七三分）。不是真正意义上的CV，没有交叉的思想，所以验证集上的测试精度与原始数据的分组有很大关系，具有随机性，不具有说服性。（是否可通过多次平均的方法来消除这种随机性？待验证）

2. K-fold CV

 

一般，k>=2。经验上，k取5即可（计算量与精度的权衡），k=5时的结果大致和10以上类似。

3. Leave-one-out CV（LOO-CV）

K-fold CV 的极端情况，将k设为样本数。

优点：（1）结果可靠。

     （2）实验过程可被复制。

缺点：计算量过大。实际操作困难，除非并行化。

 

实验: 使用高斯核最小二乘做回归。

Code:

Contents

• training set
• test set
• ================Cross Validation=======================
• ================ Normal Equations ================

training set

the number of the tarining samples

trainSize=1000;
% the dimension of the tarining samples
trainDim=1;

% the gaussian noise (u=0, sigma= 0.4472(variance equals to 0.2))
% epsilon=normrnd(0, 0.4472,trainSize,trainDim);

% the gaussian noise (u=0, sigma= 0.3162(variance equals to 0.1))
% epsilon=normrnd(0, 0.3162,trainSize,trainDim);

epsilon=normrnd(0, 0.1,trainSize,trainDim);
% the nosiy training samples
% the uniform distribution in [-a,a]
% R = a - 2*a*rand(m,n)
%  x_train=1-2.*rand(trainSize,trainDim); %[-1,1]
x_train=pi-(2*pi).*rand(trainSize,trainDim); %[-pi,pi]
% sinc target function
y_train=sinc(x_train)+epsilon;
%y_train=sinc(x_train);

test set

the number of the test samples

testSize=1000;
% the dimension of the tarining samples
testDim=1;

% the test samples
x_test=pi-2*pi.*rand(testSize,testDim);
y_test=sinc(x_test);

================Cross Validation=======================

[mse,bestk,bestg] = RLScgForRegress(x_train,y_train);

================ Normal Equations ================

fprintf('Solving with normal equations...\n');

D_train=generateDictonary(x_train,x_train,bestg);

D_test=generateDictonary(x_test,x_train,bestg);

% Map D_train onto Guassian high-dim Features and Normalize
[D_train, mu, sigma] = featureNormalize(D_train);

% Map D_test and normalize (using mu and sigma)
D_test = bsxfun(@minus, D_test, mu);
D_test = bsxfun(@rdivide, D_test, sigma);

% Calculate the parameters from the normal equation
ntheta = normalEqn(D_train,y_train,bestk);

%     % Display normal equation's result
%     fprintf('Theta computed from the normal equations: \n');
%     fprintf(' %f \n', ntheta);
%     fprintf('\n');


trainError=sqrt(sum((y_train-D_train*ntheta).^2)/size(y_train,1));
testError=sqrt(sum((y_test-D_test*ntheta).^2)/size(y_test,1));


%  Plot fit over the data
figure;
plot(x_test, y_test, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
xlabel('x test');
ylabel('y test');
hold on;
grid on;
plot(x_test,D_test*ntheta, 'b.', 'LineWidth', 2);
hold off;

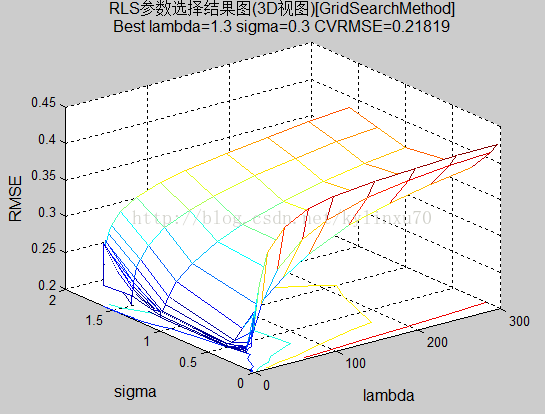
对于这个问题，选择K为多少比较合适？

1、 首先确定待选模型参数的范围（即假设空间），确保所选范围能包含最优假设。K-fold CV 可以选出某种意义下的最优的参数，但通过实验观察，似乎的趋势是，不同的K对应的假设空间是不同的，K越大，需要增加参数的区间，以保证假设空间能包含住最优性能的假设。

 

Eg：lambda_vec = [0.001 0.003 0.01 0.03 0.1 0.3 1 1.3 1.6 1.9 2.3 3 6 10 20 40 70 100 150 200 250 300];

sigma_vec = [0.03 0.1 0.3 1 1.3 1.6];

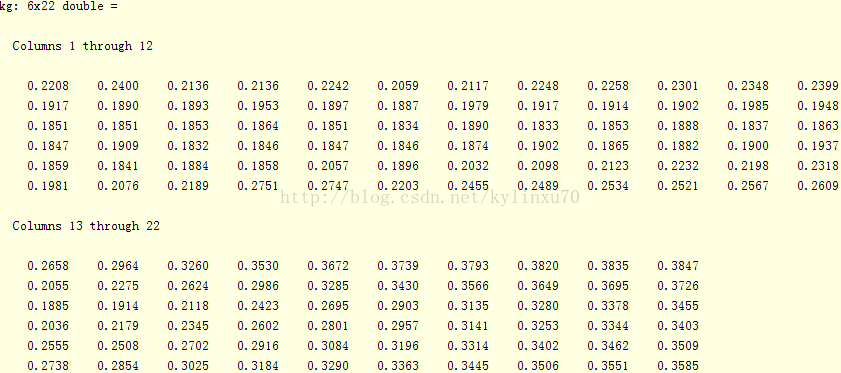
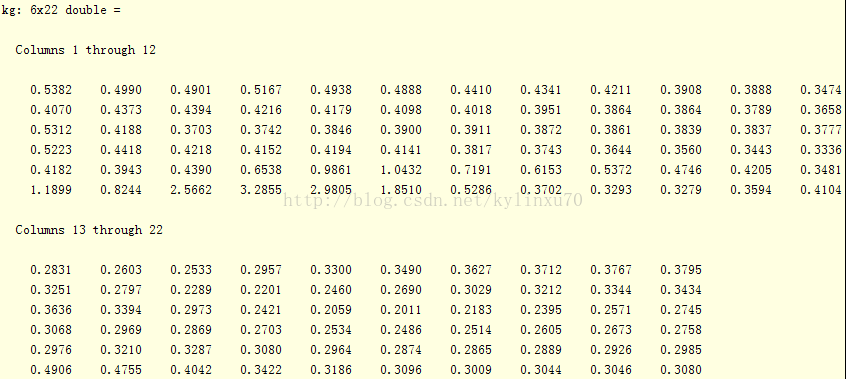
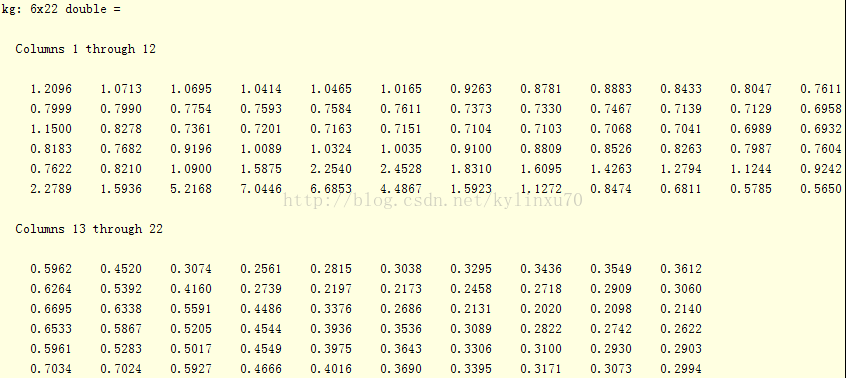
这两组参数区间下，对应的假设的性能：

 

 

2、 对于不同的K对应的CV的评价指标：

（1）CV意义下的估计泛化误差（使用RMSE）

（2）实际泛化误差

 

K=2时

最优估计泛化误差         0.1832                实际泛化误差 0.1769

K=5时

最优估计泛化误差         0.2011                实际泛化误差 0.2571

 

K=10时

 

最优估计泛化误差         0.2020                实际泛化误差 0.2740

 

 

这种随着K增加，泛化误差增加的趋势和理论上不符？

理论上，随着K越大，可供训练的样本更多，这样评估的结果更可靠。即是这两种泛化误差都应是下降趋势。