吴恩达机器学习笔记

本文为吴恩达机器学习视频听课笔记，仅记录课程大纲及对于部分关键点、疑难点的理解。
课程链接: 吴恩达机器学习.

说明：这篇博客已经躺在草稿箱里很久了 由于整理公式等耗费大量时间 仅仅梳理了前 7章的内容 后续内容若有时间再做整理

Chapter1 绪论

本章主要介绍了机器学习的定义、算法分类及应用场景。

Chapter2 单变量线性回归

模型表示

• 符号说明

项目	Value
m	Number of training examples
x’s	“input” variable
y’s	“output” variable
(x,y)	one training example
($x^{(i)}$,$y^{(i)}$)	the $i^{th}$ training example

• 监督学习算法工作过程
  

• Linear Regression Model

  $h_{\theta }(x)={\theta }_0+{\theta }_{1}x$

  $\mathrm{J}({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$

代价函数

项目	Value
假设函数	$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$
参数	${\theta }_0$, ${\theta }_1$
代价函数	$\mathrm{J}({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$
目标	$minimize\mathrm{J}({\theta }_0,{\theta }_1)$

注意：

• 选择合适的${\theta }_0$,和${\theta }_1$使得假设函数表示的直线更好地与数据点拟合，定义为最小化问题
• 代价函数中，系数为$\frac{1}{2}$，目的是在梯度下降时便于求解

梯度下降

（一种可以自动找到使得函数J最小的参数的算法）

1. 定义：
   repeat until convergence{
   ${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}\mathrm{J}({\theta }_0,{\theta }_1)$        (for j=0 and j=1)
   }
2. 关于α（学习率）
   （1）学习率表示在控制梯度下降时，以多大的幅度更新参数（采用同时更新的方法，即 ${\theta }_0$和${\theta }_1$同时更新）
   （2）if α is too small, gradient descent can be slow
   （3）if α is too large, gradient descent can overshoot the minimum. It may fail to converge, or even diverge.

线性回归中的梯度下降

1. 线性回归模型

   $h_{\theta }(x)={\theta }_0+{\theta }_{1}x$

   $\mathrm{J}({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$

2. 梯度下降算法

   repeat until convergence{
   ${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}\mathrm{J}({\theta }_0,{\theta }_1)$        (for j=0 and j=1)
   }

3. Apply gradient descent to minimize squared error cost function

   求偏导：
   $\frac{\partial }{\partial {\theta }_j}\mathrm{J}({\theta }_0,{\theta }_1)=\frac{\partial }{\partial {\theta }_j}\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2=\frac{\partial }{\partial {\theta }_j}\frac{1}{2m}\sum _{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}{)}^2$

   j=0时 ，$\frac{\partial }{\partial {\theta }_0}\mathrm{J}({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$
   j=1时 ，$\frac{\partial }{\partial {\theta }_1}\mathrm{J}({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$
   结果：
   repeat until convergence{
   ${\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$
   ${\theta }_1:={\theta }_1-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$
   }

Chapter3 线性代数回顾

1. 矩阵和向量
   （1）矩阵（Matrix）：由数字组成的矩形阵列（Rectangular array of numbers）
   矩阵的维度（Dimension of matrix）： 矩阵的行数乘以列数（Number of rows × number of columns）
   矩阵的项（Entry）：$A_{ij}$=" i,j entry" in the $i_{th}$ row, $j_{th}$ column.
   Function：矩阵提供了一种快速整理、索引和访问大量数据的方式
   （2）向量（Vector）：一种特殊的矩阵（An n×1 matrix ）
2. 矩阵的加减法、乘法
   （1）加减法：两个矩阵的每一个元素逐个相加减（只有相同维度的矩阵才能相加）
   （2）标量乘法：将矩阵中所有元素逐一与3相乘（标量，在这里指的是实数）
   （3）乘法：条件：第一个矩阵的列数等于第二个矩阵的行数；相乘得到的结果： 行数等于第一个矩阵的行数，列数等于第二个矩阵的列数；矩阵的乘法不符合交换律，符合结合律
   （4）单位矩阵：对角线元素为1，其他位置为0
3. 逆和转置
   （1）逆矩阵：
   if A is an m×m matrix, and if it has an inverse, $A{A}^{-1}=A^{-1}A=I$.
   （2） 矩阵的转置
   Let A be an m×n matrix, and let B=$A^T$. Then B is an n×m matrix, and $B_{ij}=A_{ji}$.

Chapter4 多变量线性回归

Notation

项目	Value
n	number of features
$x^{(i)}$	input of $i^{th}$ training example
$x_j^{(i)}$	value of feature j in $i^{th}$ training example

假设函数：$h_{\theta }(x)={\theta }^{T}x={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n$ 其中，$x_0=1$

参数：θ ，为n+1维向量

代价函数： $\mathrm{J}(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$

多变量梯度下降法

（使用梯度下降法处理多元线性回归）
Repeat {
${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$       ( simultaneously update ${\theta }_j$ for j = 0,…,n )
}
注意：

1. 特征缩放：
   由于各特征值范围不一，可能影响代价函数的收敛速度。通过特征缩放，使得他们的值的范围更相近，这样，收敛所需的迭代次数更少。
   Feature Scalling：Get every feature into approximately a -1 ≤ $x_i$ ≤ 1 range.
   方法：
   （1）将特征值除以最大值
   （2）归一 法
   $x_i=\frac{x_i-avg(x)}{max(x)-min(x)}$
2. 如何选择学习率？
   通过绘制代价函数随迭代步数变化的曲线，确定学习率的取值。
   If α is too small：slow convergence
   If α is too large：J(θ) may not decrease on every iteration;may not converge.
   To choose α, try…,0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1,…

正规方程法

（梯度下降算法需要经过梯度下降的多次迭代，获得最小代价函数J(θ)。而正规方程则不须运行迭代算法，只需一步求解θ的最优值）

1. 使用步骤：
   （1）构建矩阵X、向量y。本例中，矩阵X维度为：m×(n+1)；y为m维向量
   （2）利用公式求解最优θ值（最小化线性回归的代价函数J(θ)）
   注意：
   使用正规方程法不需要特征缩放
2. 梯度下降法与正规方程法的区别
   （1）梯度下降需要选择学习率α，而正规方程法不需要
   （2）梯度下降算法需要多次迭代，而正规方程法不需要
   （3）由于逆矩阵计算代价较高(以矩阵维度的三次方增长，$X^{T}X$维度为n×n时，代价为O($n^3$))。因此，当n的值很大时，正规方程方法运行慢。故当特征数目<=10000时，选用正规方程法；当特征数目n>10000时，选用梯度下降方法
   （4）在线性回归模型中，正规方程方法适用（并且比梯度下降算法更快）；在一些更复杂的算法中（例如分类算法、logistic回归算法），正规方程并不适用

多项式回归

（使用线性回归的方法来拟合复杂函数、甚至非线性函数）

例：
$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3={\theta }_0+{\theta }_1(size)+{\theta }_2(size{)}^2+{\theta }_3(size{)}^3$

$h_{\theta }(x)={\theta }_0+{\theta }_1(size)+{\theta }_2\sqrt{(size)}$

在使用多项式回归时，注意特征的缩放

Chapter 5 逻辑回归

逻辑回归是一种常用的分类算法，其输出值永远在 0 到 1 之间。

假设函数

定义：

$h_{\theta }(x)=g({\theta }^{T}x)$

其中， $h_{\theta }(x)$ 的范围为 (0,1)

其含义为：$x$ 及 θ 情况下，y = 1 的可能性

$h_{\theta }(x)=P(y=1|x;\theta )=1-P(y=0|x;\theta )$

将sigmoid函数$g(z)=\frac{1}{1+e^{-z}}$代入逻辑回归模型，得到：

$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$

决策边界

决策边界即为分类的边界线

举例：

代价函数

$\mathrm{J}(\theta )=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x),y^{(i)})$

$Cost(h_{\theta }(x),y)=-log(h_{\theta }(x))$     if y=1

$Cost(h_{\theta }(x),y)=-log(1-h_{\theta }(x))$     if y=0

简化：

对于二元分类问题：

$Cost(h_{\theta }(x),y)=-ylog(h_{\theta }(x))-(1-y)log(1-h_{\theta }(x))$

$\mathrm{J}(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$

梯度下降

（最小化代价函数）
Repeat {
${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )$
}
(simultaneously update all ${\theta }_j$)

解偏导得：
Repeat {
${\theta }_j:={\theta }_j-\alpha \sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$
}
(simultaneously update all ${\theta }_j$)
区分：
线性回归与Logistic回归的梯度下降算法中，更新规则形式相同，但其中假设函数hθ(x)的含义不同。
线性回归中，$h_{\theta }(x)={\theta }^{T}x$ ；Logistic回归中，$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$ 。
除梯度下降外，还有其他优化算法：
Conjugate gradient
BFGS
L-BFGS
以上三种方法不需要手动选择学习率，相比梯度下降更快，但更加复杂。

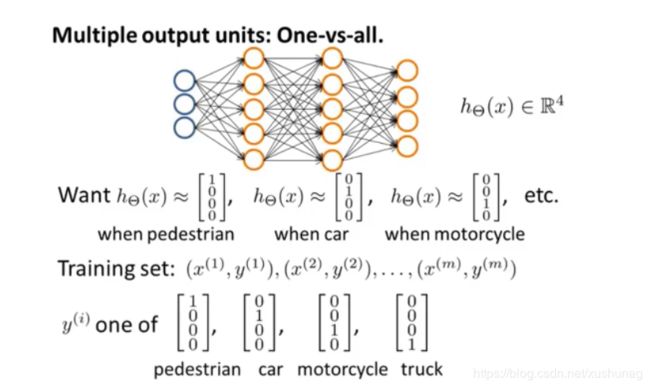
多类别分类问题

原理：转化成多个二元分类问题
Train a logistic regression classifier $h_{\theta }^{(i)}(x)$ for each class i to predict the probability that y=i.
On a new input x, to make a prediction, pick the class i that maximizes.（即选出k个分类器中可信度最高、效果最好的）
$h_{\theta }^{(i)}(x)=p(y=i|x;\theta )$   i=(1,2,3…k)
其中，k表示类别数量；$h_{\theta }^{(i)}(x)$表示输出 y=i 的可能性

Chapter6 正则化

过拟合问题

欠拟合（Underfitting）：不能很好地拟合训练数据
过拟合（Overfitting）：过度地拟合了训练数据，而没有考虑到泛化能力
解决过拟合问题的方法：
解决过拟合问题：
（1） 减少变量数量
人工检查变量清单，选择要保留的变量/ 模型选择算法
（2）正则化
基本思想：惩罚各个参数大小，降低模型复杂度，改善或减少过拟合问题。

正则化代价函数

$\mathrm{J}(\theta )=\frac{1}{2m}[\sum _{i=1}^m({h_{\theta }(x^{(i)})-y^{(i)})}^2-\lambda \sum _{j=1}^n{{\theta }_j}^2]$
其中，

$\lambda {\sum }_{j=1}^n{{\theta }_j}^2$为正则化项

正则化参数λ：控制两个目标（更好地拟合训练集的目标、将参数控制得更小）之间的平衡关系

线性回归、逻辑回归的正则方法

将正则化的思想用在线性回归和Logistic回归，来避免过拟合问题。

一、线性回归正则化

拟合线性回归模型的两种算法：
（1）梯度下降
Repeat {
${\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_0^{(i)}$
${\theta }_j:={\theta }_j-\alpha [\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_j]$
}
（2）正规方程
$X=\left[\begin{array}{c}(x^{(1)}{)}^T\\ ...\\ ...\\ (x^{(m)}{)}^T\end{array}\right]$

$y=\left[\begin{array}{c}{y}^{(1)}\\ ...\\ ...\\ y^{(m)}\end{array}\right]$

$\theta =(X^{T}X+\lambda M{)}^{-1}{X}^{T}y$

M为(n+1)*(n+1)矩阵：

$M=\left[\begin{array}{cccc}0& & & \\ & 1& & \\ & & ...& \\ & & & 1\end{array}\right]$

二、逻辑回归正则化

正则化的逻辑回归代价函数：

$\mathrm{J}(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log(h_{\theta }(x^{(i)}))+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j]$

正则化的逻辑回归梯度下降算法：
Repeat {
${\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_0^{(i)}$
${\theta }_j:={\theta }_j-\alpha [\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_j]$
}

Chapter7 神经网络

背景

在特征过多的情况下，简单逻辑回归算法不适合学习复杂非线性假设。而神经网络可以处理特征量过大的情况。

• 神经网络起源：人们尝试设计模仿大脑的算法
• 广泛应用：1980s-1990s
• 没落：1990后期
• 再次兴起：重要原因： 计算机运行速度变快

模型表示

类比大脑神经元，树突表示输入，接受来自其他神经元的信息；细胞核表示激活单元；轴突表示输出，向其他神经元传递信号。

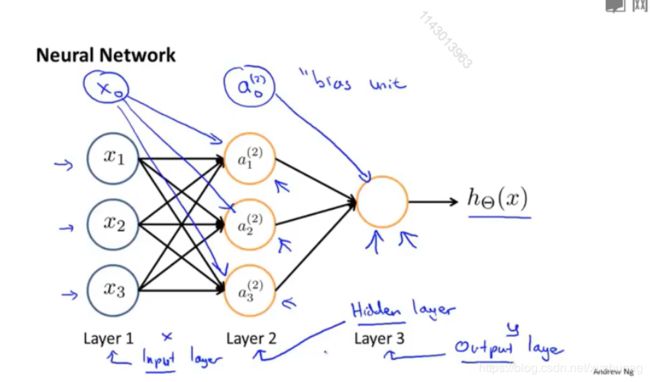
符号说明：

项目	Value
输入层	对应训练集中的特征$x$
输出层	对应训练集中的结果$y$
$x_0$	值为1，偏置单元，根据具体例子中是否方便选择加或不加$x_0$
activation function	激活函数，非线性函数g(z)
θ	参数（parameters），文献中也称为权重（weights）
$a_i^{(j)}$	第$j$层的第$i$个激活单元
${\theta }^{(j)}$	第$j$层映射到第$j+1$层的权重矩阵

计算：
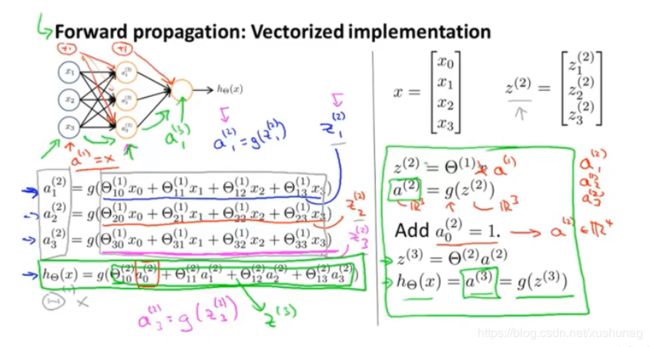
（1）前向传播

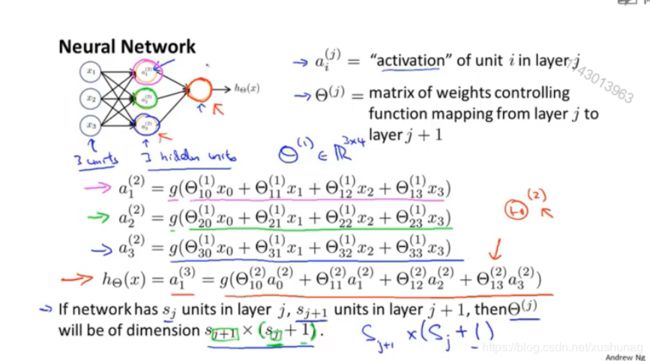
注：
逻辑回归使用原始的$x_1,x_2,x_3$作为特征
神经网络使用隐藏层计算的数值$a_1^{(2)}，a_2^{(2)}，a_3^{(2)}$作为特征
（2）计算h(x)的高效方法：向量化

多元分类

利用神经网络解决多类别分类问题

输出层输出单元个数即为类别数