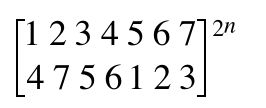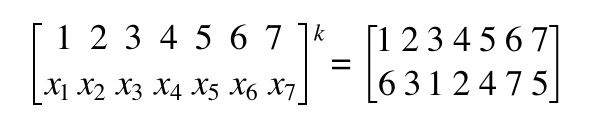ACM 置换群专题（1）

关于置换群的题目下面列举几个：
POJ 2369 Permutations
题目还是比较简单的，就是一次求出每个循环节的长度，取它们的公倍数即可

//
//  main.cpp
//  poj 2369 Permutations
//
//  Created by ccccsober on 7/2/16.
//  Copyright © 2016 cccsober. All rights reserved.
//
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int MAX1= (1e3) +2 ;
//const int MAX2=    ;
//const int Mod=     ;
const double plus=0.49999999;
const int INF=0x3f3f3f3f;
typedef long long LL;
typedef unsigned long long ULL;
#define M_PI 3.141592653589
int num[MAX1];
bool vis[MAX1];
int gcd(int a,int b){
    return b==0?a:gcd(b,a%b);
}
int lcm(int a,int b){
    return a/gcd(a,b)*b;
}
int main(int argc, const char * argv[]) {
    int n;
    while(scanf("%d",&n)!=EOF){
        for(int i=1;i<=n;i++)
            scanf("%d",&num[i]);
        int ans=1;
        for(int i=1;i<=n;i++){
            int t=i;
            int cnt=0;
            while(!vis[t]){
                vis[t]=1;
                t=num[t];
                cnt++;
            }
            if(cnt)
            ans=lcm(ans,cnt);
        }
        cout<


POJ 1026 Cipher
 题目总体还是比较简单，算出每个置换群的阶，依次算出每个 k%loopsize[i] 就能得到结果了，下面相对详细的讲解下：
 题目中：
 {1 2 3 4 5 6 7 8 9 10}
 ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ⇒{1,4,7},{2,5},{3},{6,8},{9,10}
 {4 5 3 7 2 8 1 6 10 9} ⇒loopsize[10]={3,2,1,3,2,2,3,2,2,2}
求loopsize的时候可以选择递归，这个很好的。
 一开始我一直纠结算法复杂度，后来想想，一开始球loopsize的时候其实就是每个元素遍历一遍，这个不可能减少，而且也不算太高 ，在O(n)总体的复杂度也差不多。
 给出AC参考代码：就是个递归着loopsize，之后处理下，代码实际不到60行...
//
//  main.cpp
//  poj 1026 Cipher
//
//  Created by ccccsober on 7/3/16.
//  Copyright © 2016 cccsober. All rights reserved.
//

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int MAX1= 202  ;
//const int MAX2=    ;
//const int Mod=     ;
const double plus=0.49999999;
const int INF=0x3f3f3f3f;
typedef long long LL;
typedef unsigned long long ULL;
int num[MAX1];
int loopsize[MAX1];
bool vis[MAX1];
char result[MAX1];
char str[MAX1];
#define M_PI 3.141592653589
void recursion(int i,int& n){
    if(!vis[i]){
        vis[i]=1;
        n++;
        recursion(num[i],n);
    }
    loopsize[i]=n;
}
void _init(){
    memset(vis,0,sizeof(vis));
}
void _init2(){
    memset(result,0,sizeof(result));
    memset(str,0,sizeof(str));
}
int main(int argc, const char * argv[]) {
    freopen("/Users/sperc4/Desktop/input.txt", "r", stdin);
    int n;
    while(scanf("%d",&n)!=EOF){
        _init();
        if(!n) break;
        for(int i=1;i<=n;i++)
            scanf("%d",&num[i]);
        int k;
        for(int i=1;i<=n;i++){
            int t=0;
            if(!vis[i])
            recursion(i,t);
        }
        while(scanf("%d",&k),k){
            _init2();
            getchar();
            gets(str+1);
            for(int i=1;i<=n;i++){
                int t=k%loopsize[i];
                int pos=i;
                while(t--){
                    pos=num[pos];
                }
                result[pos]=str[i];
            }
            for(int i=1;i<=n;i++){
                if(result[i])
                    printf("%c",result[i]);
                else
                    printf(" ");
            }
            printf("\n");
        }
        printf("\n");
    }
    //      freopen("/Users/sperc4/Desktop/output.txt","w",stdout);
    fclose(stdin);
    //      fclose(stdout);
    return 0;
}


POJ 1721 CARDS
 题目跟我预想的并不一样...
 我开始觉得进行n次的置换那么的到应该等价下面分析：
 n=1 有
 









 那么如果是n次置换：











 我觉得既然n是1～1000，那么这里应该会用到 快速幂取模，之后的到的数学式子等价于＝











 自己在笔算的时候可以得到这样的结果：











 但说实话，直接怎样我实在是不知道如何进行了...

下面给出一个思路是别人的：
 poj 1721
 怎么说，我一开始很疑惑，为什么经过多番置换一定可以回到原来的数组...
 比如下面这个例子：
 1 2 3 4 5 6 7 8 9
 6 3 5 9 7 2 1 8 4 后来会发现是下面的情况：
 1 2 3 4 5 6 7 8 9 1 2 3 4 5 7 8 9 1 2 3 4 5 6 7 8 9
 6 3 5 9 7 2 1 8 4 ⇒ 2 5 7 4 1 6 8 9 ⇒ 5 1 6 4 2 7 3 8 9
我测试过后面总是在后面那两个中不断循环，这个置换那个循环节就是2吗？我要怎么从第一个得出他的循环节就是2？
 但仔细研究了下题目叙述的到结果是：
 这句话保证最后一定可以回到原始的状态...
 **
 Alice and Bob play a game. Alice first writes down all the numbers from 1 to N in some random order: a1, a2, ..., aN. Then she arranges the cards so that the position ai holds the card numbered ai+1, for every 1 <= i <= N-1, while the position aN holds the card numbered a1. **
 ...
 最后还是给出一个参考的代码：
 我考虑很久要不要把多余内容删掉，后来想想，留出自己的思考过程何尝不是好的足迹
//
//  main.cpp
//  poj 1721 CARDS
//
//  Created by ccccsober on 7/6/16.
//  Copyright © 2016 cccsober. All rights reserved.
//
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int MAX1=  (1e3) +3;
//const int MAX2=    ;
//const int Mod=     ;
const double plus=0.49999999;
const int INF=0x3f3f3f3f;
typedef long long LL;
typedef unsigned long long ULL;
#define M_PI 3.141592653589
int temp[MAX1];
int ans[MAX1];
int data[MAX1];
bool vis[MAX1];
//int gcd(int a,int b){
//    return b==0?a:gcd(b,a%b);
//}
//int lcm(int a,int b){
//    return a/gcd(a,b)*b;
//}
bool check_same(int*a ,int*b,int n){
    for(int i=1;i<=n;i++)
        if(a[i]!=b[i]) return false;
    return true;
}
int main(int argc, const char * argv[]) {
    freopen("/Users/sperc4/Desktop/input.txt", "r", stdin);
    int n,s;
    while(scanf("%d%d",&n,&s)!=EOF){
        memset(vis,0,sizeof(vis));
        for(int i=1;i<=n;i++){
            scanf("%d",&ans[i]);
            data[i]=ans[i];
        }
        int loopsize=1;
        for(int i=1;i<=n;i++)
            temp[i]=data[data[i]];
//            memcmp(data,temp,sizeof(temp));
        for(int i=1;i<=n;i++)
            data[i]=temp[i];
        while(!check_same(temp,ans,n)){
            loopsize++;
            for(int i=1;i<=n;i++)
                temp[i]=data[data[i]];
            for(int i=1;i<=n;i++)
                data[i]=temp[i];
        }
//        int t=0;
//        for(int i=1;i<=n;i++){
//            int k=i;
//            t=0;
//            while(!vis[k]){
//                t++;
//                vis[k]=1;
//                k=ans[ans[k]];
//            }
//            if(t)
//                loopsize=lcm(t,loopsize);
//        }
//        
        int plus=loopsize-s%loopsize;
//        cout<<"loopsize "<

POJ 3821 Leonardo's Notebook
 这个题目也不错，非常好的利用了循环群分裂的一些性质。
 比较好的论文：置换群快速幂运算+研究与探讨
 里面只看前半部分就绰绰有余了。
 因为gcd(2＊k,2)=2说明凡是置换p＊p得到的结果，其实都是由p分裂过来的。长度为奇数的置换，不用在意，因为gcd(2＊k+1,2)=1，长度为2*k 的循环，这个就是关注点了。任何一个 2＊k 必然是 4＊k分裂出现。并且又一个和它对应。那么，长度为偶数的一定是成对出现

ACM 置换群专题（1）

你可能感兴趣的:(ACM 置换群专题（1）)