多智能体强化学习博弈系列（1）- 差分博弈和模糊系统

几点说明：

1. 这个系列重点关注多智能体和强化学习在差分博弈中的应用，文章中有尝试复现的主要是双人/多人混合策略多阶段随机差分零和游戏的模拟。关于智能体、关于强化学习、关于博弈论基础的介绍，在这个系列基本不涉及。
   • 强化学习简简简介见我之前的文章。
   • 多智能体简简简介见我之前的文章。
   • 有关博弈论基础的内容，e.g. 双人/多人游戏、零和/变和游戏、单一/混合策略、单一/多阶段博弈等概念，本文不涉及，有兴趣的童鞋可以参考这里。
   • 这个系列也不涉及各种均衡的求解。
2. 希望更多关注神经网络类实现的童鞋可以不必再往下读了：本系列不涉及DQN或其他类型的由神经网络实现的RL系统。

差分博弈 differential games

在真实世界中经常遇到环境、状态、行为都处于连续空间的情况。这时一般选择用差分方程来表达连续空间。这类博弈成为差分博弈，在这种博弈中智能体的目标是学习如何适应和学习连续可变的环境和能力。

模糊系统 fuzzy systems

模糊系统通常使用离散空间（比如文字描述）作为标签表示状态或行为。方法是通过构造membership function。

定义Universe of discourse $X$ 为一组元素x的集合，所有集合中的元素具有相同的特征标签。

定义membership function (MF) ${\mu }_A(x)$ 为映射集合元素到0-1的空间的方程。如果${\mu }_A(x)$取值仅为0或1, 这个模糊集合称为crisp或classical集合：

$$A=\{(x,{\mu }_A(x))|x\in X\}$$

membership function的交集intersection运算：

$${\mu }_{A\cap B}(x)=T({\mu }_A(x),{\mu }_B(x))={\mu }_A(x)\ast {\mu }_B(x)$$

其中$T$是泛化的t-norm运算符，代表比如如下运算:

• 求最小: $T_{min}(a,b)=min(a,b)$
• 代数乘积: $T_{ap}(a,b)=ab$

并集union运算：

$${\mu }_{A\cup B}(x)=S({\mu }_A(x),{\mu }_B(x))={\mu }_A(x)\dot{+}{\mu }_B(x)$$

其中$S$是泛化的s-norm运算符，代表比如如下运算：

• 求最大：$S_{max}(a,b)=max(a,b)$
• 代数求和：$S_{ap}(a,b)=a+b-ab$

一些常用的membership function: singleton, gaussian, sigmodial, triangular, etc.

Fuzzy IF-THEN rules：用来实现不确定环境下的专家系统建模的一组规则：

${\mathfrak{R}}_l$ : if x is A then y is B

其中 x, y是模糊变量，A 和 B是定义在空间X和Y的模糊集合，"x is A"称为_antecedent_ 或 premise, “y is B” 称为 consequence 或 conclusion.

generalized modus ponens 定义为：

premise1(rule): if x is A then y is B
premise2(fact): x is A’
conclusion: y is B’.

定义fuzzy inference engine 为一个可以组合多个模糊IF-THEN规则的推理系统，目的是将模糊规则映射到模糊集合。

Product inference engine：一种常见的模糊推理系统，通常包含以下三个特征：

• T运算是代数乘积，S运算是求最大值
• 使用Mamdani’s product implication (后面有介绍）
• 推理系统使用交集作为模糊规则的组合方式

Mamdani implication: 将模糊规则$l$作为二进制的模糊关系处理：

$${\mu }_R(x,y)={\mu }_{A^l\times B^l}(x,y)={\mu }_{A^l\to B^l}(x,y)={\mu }_{A^l}(x)\ast {\mu }_{B^l}(x)$$

其中$A^l\to B^l$是模糊关系的映射关系。在product inference engine 中，"*"代表代数乘积。

根据以上定义，一个模糊集合$B^{{}^{\prime }l}$可以这样被推理出来：

$${\mu }_{B^{{}^{\prime }l}}(y)=su{p}_{x\in X}T[{\mu }_{A^{\prime }}(x),{\mu }_{A^l\to B^l}(x,y)]$$

其中T[.]为t-norm运算符，sup为最大元素。有：

${\mu }_{B^{\prime }}(y)=ma{x}_{l=1}^M{\mu }_{B^{{}^{\prime }l}}(y)$

          $=ma{x}_{l=1}^M\left[su{p}_{x\in X}\left({\mu }_{A^{\prime }}(x){\Pi }_{j=1}^n{\mu }_{A_j^l}(x_j){\mu }_{B^l}(y)\right)\right]$

其中$l\in M$是规则，M是规则集合，j是antecedents的索引, $n$是每个premise里的antecedent个数。$A_j^l$是antecedent中用于第l个规则的第j个模糊集合，$B^l$是第l个规则的推理结果（consequence）。

举例：

Premise 1 (rule 1): if $x_1$ is $A_1^1$ and $x_2$ is $A_2^1$ then y is $B^1$ (j = (1,2), l = 1)
Premise 2 (rule 2): if $x_1$ is $A_1^2$ and $x_2$ is $A_2^2$ then y is $B^2$ (j = (1,2), l = 2)
Premise 3 (fact): $x_1$ is $A_1^{\prime }$ and $x_2$ is $A_2^{\prime }$
Conclusion: y is $B^{\prime }$

模糊系统构建：

一个模糊系统(FIS/fuzzy contollers)的结构：

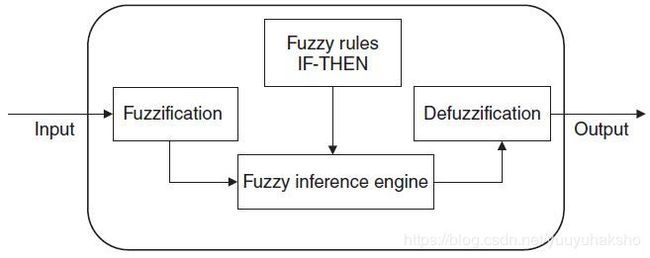
参考 “Multi-Agent Machine-Learning - A Reinforcement Approach” - Howard M. Schwartz.

模糊化Fuzzifier: 将连续输入空间映射到离散的membership function上，并用membership degree代表映射的强度。

以singleton membership function为例：

$${\mu }_A(x)=\{\begin{array}{ll}1& \text{if }x=x^{\ast }\\ 0& \text{otherwise}\end{array}$$

其中$x^{\ast }$是一个连续的值。

以Gaussian membership function为例:

$${\mu }_A(x)=e^{-(\frac{x_1-x_1^{\ast }}{a_1}{)}^2}\ast \cdots \ast e^{-(\frac{x_n-x_n^{\ast }}{a_n}{)}^2}$$

其中$a$是正的常量。

以 triangular membership function为例：

$${\mu }_A(x)=\{\begin{array}{ll}(1-\frac{|x_1-x_1^{\ast }|}{b_1})\ast \cdots \ast (1-\frac{|x_n-x_n^{\ast }|}{b_n})& \text{if }|x_i-x_i^{\ast }|\ge b_i\\ 0& \text{otherwise}\end{array}$$

其中$b_i$是一个正的常量。

去模糊化Defuzzifier: 将模糊的值重新映射回连续空间。常用的方法之一是加权平均去模糊化，计算量少好理解：

$$f=\frac{{\sum }_{l=1}^M\left({\Pi }_{j=1}^J{\mu }^{A_j^l}(x_j)\right)f_l}{{\sum }_{l=1}^M\left({\Pi }_{j=1}^J{\mu }^{A_j^l}(x_j)\right)}$$

其中J是输入个数，M是规则个数。

更多去模糊化方法参考这里。

下一篇会介绍如何实现一个行走在连续状态和行为空间中，用加强学习方法寻找博弈中的纳什均衡点的智能体。这个智能体所使用的算法的输入和输出都经过了模糊系统的离散化和去离散化处理。