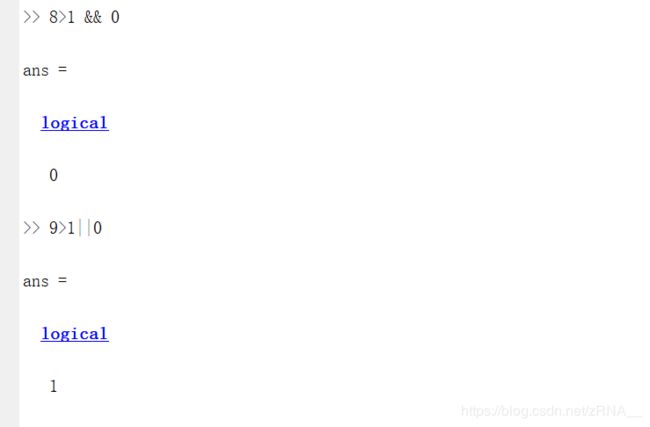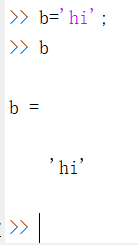matlab版吴恩达机器学习第五章笔记
机器学习matlab操作基础
- 1、基本操作
- 2、移动数据
- 3、计算数据
- 4、绘图数据
- 5、控制语句:for,while,if语句
- 6、向量化
1、基本操作
参考视频: 5 - 1 - Basic Operations (14 min).mkv
打开matlab(R2019b) 这是 matlab命令行
现在示范最基本的matlab代码:
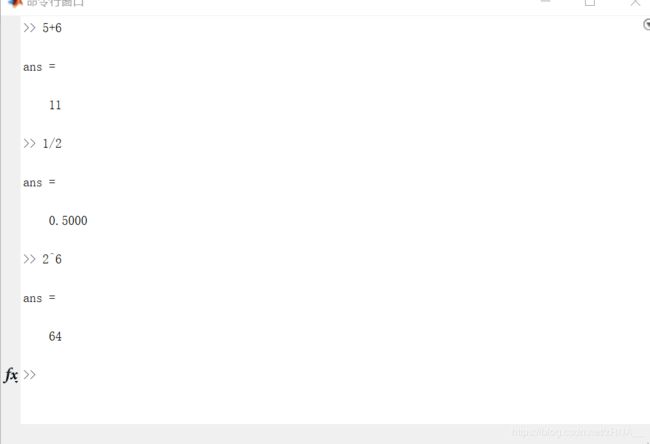
输入5 + 6,然后得到11。
输入1/2、2^6等等,得到相应答案。
这些都是基本的数学运算
也可以去做逻辑运算 例如 1==2 计算结果为 false(假)这里用0表示 1~=2 计算结果为 true(真)用1表示
![]()
请注意,不等于符号的写法是这个波浪线加上等于符号 ( ~= ),而不是等于感叹号加等号( != ),这是和其他一些编程语言中不太一样的地方。
让我们看看逻辑运算 1 && 0,使用双&符号表示逻辑与,1 && 0判断为假,1和0的或运算 1 || 0,其计算结果为真。
还有异或运算 如XOR ( 1, 0 ),其返回值为1
如果你想分配一个变量,但不希望在屏幕上显示结果,你可以在命令后加一个分号,可以抑制打印输出,敲入回车后,不打印任何东西。
现在举一个字符串的例子:变量b等于"hi"。
c等于3大于等于1,所以,现在变量c的值是真。
如果你想打印出变量,或显示一个变量,你可以像下面这么做:
设置a等于圆周率,如果我要打印该值,那么只需键入a像这样 就打印出来了。
对于更复杂的屏幕输出,也可以用DISP命令显示:


这是一种,旧风格的C语言语法,对于之前就学过C语言的同学来说,你可以使用这种基本的语法来将结果打印到屏幕。
例如 ^{T}命令的六个小数:0.6%f ,a,这应该打印的6位小数形式。
也有一些控制输出长短格式的快捷命令:
下面,让我们来看看向量和矩阵:
比方说 建立一个矩阵 A:
对A矩阵进行赋值,考虑到这是一个三行两列的矩阵,你同样可以用向量。
建立向量V并赋值1 2 3,V是一个行向量,或者说是一个3 ( 列 )×1 ( 行 )的向量,或者说,一行三列的矩阵。
如果我想,分配一个列向量,我可以写“1;2;3”,现在便有了一个3 行 1 列的向量,同时这是一个列向量。
下面是一些更为有用的符号,如:
V=1:0.1:2
这个该如何理解呢:这个集合是一组值,从数值1开始,增量或说是步长为0.1,直到增加到2,按照这样的方法对向量V操作,可以得到一个行向量,这是一个1行11列的矩阵,其矩阵的元素是1 1.1 1.2 1.3,依此类推,直到数值2。
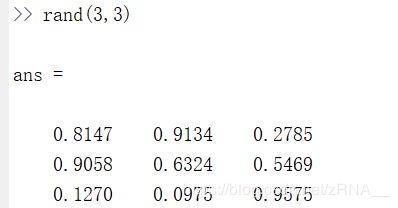
我也可以建立一个集合并用命令“1:6”进行赋值,这样V就被赋值了1至6的六个整数。
这里还有一些其他的方法来生成矩阵
例如“ones(2, 3)”,也可以用来生成矩阵:
你可以把这个方法当成一个生成矩阵的快速方法。
w为一个一行三列的零矩阵,一行三列的A矩阵里的元素全部是零:

还有很多的方式来生成矩阵。
如果我对W进行赋值,用Rand命令建立一个一行三列的矩阵,因为使用了Rand命令,则其一行三列的元素均为随机值,如“rand(3,3)”命令,这就生成了一个3×3的矩阵,并且其所有元素均为随机。
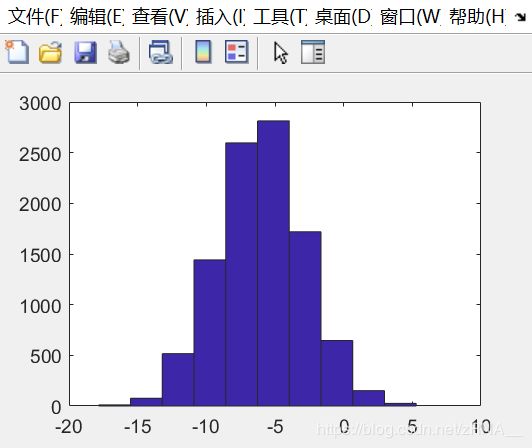
如果,你知道什么是高斯随机变量,或者,你知道什么是正态分布的随机变量,你可以设置集合W,使其等于一个一行三列的矩阵N,并且,来自三个值,一个平均值为0的高斯分布,方差或者等于1的标准偏差。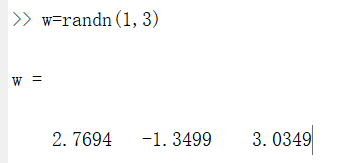 还可以设置地更复杂:
还可以设置地更复杂:
并用hist命令绘制直方图。
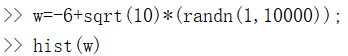
![]()
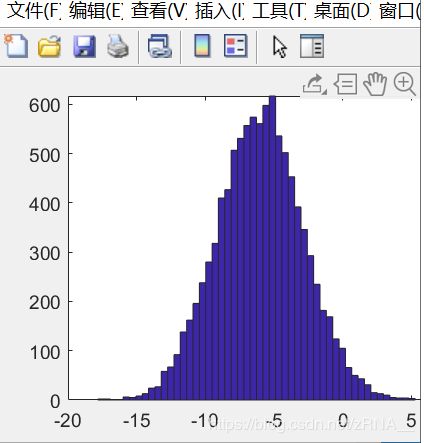
绘制单位矩阵:![]()
如果对命令不清楚,建议用help命令:
![]()
以上讲解的内容都是matlab的基本操作。希望你能通过上面的讲解,自己练习一些矩阵、乘、加等操作,将这些操作在matlab中熟练运用。
在接下来的视频中,将会涉及更多复杂的命令,并使用它们在matlab中对数据进行更多的操作。
2、移动数据
如果你有一个机器学习问题,你怎样把数据加载到 Octave 中?
怎样把数据存入一个矩阵?
如何对矩阵进行相乘?
如何保存计算结果?
如何移动这些数据并用数据进行操作?
进入我的 matlab 窗口,
我键入A,得到我们之前构建的矩阵A ,也就是用这个命令生成的:
A = [1 2; 3 4; 5 6]
这是一个3行2列的矩阵,Octave 中的 size() 命令返回矩阵的尺寸。
所以 size(A) 命令返回3 2

实际上,size() 命令返回的是一个 1×2 的矩阵,我们可以用 来存放。
设置 sz = size(A)
因此 sz就是一个1×2的矩阵,第一个元素是3,第二个元素是2。
所以如果键入 size(sz) 看看 sz的尺寸,返回的是1 2,表示是一个1×2的矩阵,1 和 2分别表示矩阵sz的维度 。
你也可以键入 size(A, 1),将返回3,这个命令会返回矩阵A的第一个元素,矩阵的第一个维度的尺寸,也就是 A矩阵的行数。
同样,命令 size(A, 2),将返回2,也就是 A矩阵的列数。
如果你有一个向量 v,假如 v = [1 2 3 4],然后键入length(v),这个命令将返回最大维度的大小,返回4。
你也可以键入length(A),由于矩阵是一个3×2的矩阵,因此最大的维度应该是3,因此该命令会返回3。
但通常我们还是对向量使用 命令,而不是对矩阵使用 length 命令,比如 length([1;2;3;4;5]),返回5。
如何在系统中加载数据和寻找数据:
当我们打开 Matlab 时,我们通常已经在一个默认路径中,这个路径是 matlab的安装位置,pwd 命令可以显示出matlab 当前所处路径。
cd命令,意思是改变路径,我可以把路径改为C:\Users\ang\Desktop,这样当前目录就变为了桌面。
如果键入 ls,ls 来自于一个 Unix 或者 Linux 命令,ls命令将列出我桌面上的所有路径。
事实上,我的桌面上有两个文件:featuresX.dat 和priceY.dat,是两个我想解决的机器学习问题。
featuresX文件如这个窗口所示,是一个含有两列数据的文件,其实就是我的房屋价格数据,数据集中有47行,第一个房子样本,面积是2104平方英尺,有3个卧室,第二套房子面积为1600,有3个卧室等等。
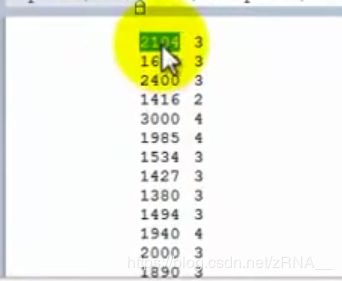
priceY这个文件就是训练集中的价格数据,所以 featuresX 和priceY就是两个存放数据的文档,那么应该怎样把数据读入 matlab 呢?我们只需要键入featuresX.dat,这样我将加载了 featuresX 文件。同样地我可以加载priceY.dat。其实有好多种办法可以完成,如果你把命令写成字符串的形式load('featureX.dat'),也是可以的,这跟刚才的命令效果是相同的,只不过是把文件名写成了一个字符串的形式,现在文件名被存在一个字符串中。matlab中使用引号来表示字符串。
另外 who 命令,能显示出 在我的 Matlab工作空间中的所有变量
所以我可以键入featuresX 回车,来显示 featuresX
还可以键入 size(featuresX),得出的结果是 47 2,代表这是一个47×2的矩阵。
类似地,输入 size(priceY),结果是 47
1,表示这是一个47维的向量,是一个列矩阵,存放的是训练集中的所有价格 Y Y Y 的值。
who 函数能让你看到当前工作空间中的所有变量,同样还有另一个 whos命令,能更详细地进行查看。
同样也列出我所有的变量,不仅如此,还列出了变量的维度。
double 意思是双精度浮点型,这也就是说,这些数都是实数,是浮点数。
如果你想删除某个变量,你可以使用 clear 命令,我们键入 clear featuresX,然后再输入 whos 命令,你会发现 featuresX 消失了。
另外,我们怎么储存数据呢?
我们设变量 V= priceY(1:10)
这表示的是将向量 Y Y Y 的前10个元素存入 V V V中。
假如我们想把它存入硬盘,那么用 save hello.mat v 命令,这个命令会将变量 V V V存成一个叫 hello.mat 的文件,让我们回车,现在我的桌面上就出现了一个新文件,名为hello.mat。
现在我们清除所有变量,直接键入clear,这样将删除工作空间中的所有变量,所以现在工作空间中啥都没了。
但如果我载入 hello.mat 文件,我又重新读取了变量 v v v,因为我之前把变量 v v v存入了hello.mat 文件中,所以我们刚才用 save命令做了什么。这个命令把数据按照二进制形式储存,或者说是更压缩的二进制形式,因此,如果 v v v是很大的数据,那么压缩幅度也更大,占用空间也更小。如果你想把数据存成一个人能看懂的形式,那么可以键入:
save hello.txt v -ascii
这样就会把数据存成一个文本文档,或者将数据的 ascii 码存成文本文档。
我键入了这个命令以后,我的桌面上就有了 hello.txt文件。如果打开它,我们可以发现这个文本文档存放着我们的数据。
这就是读取和储存数据的方法。
接下来我们再来讲讲操作数据的方法:
假如 A A A 还是那个矩阵
跟刚才一样还是那个 3×2 的矩阵,现在我们加上索引值,比如键入 A(3,2)
这将索引到 A A A 矩阵的 (3,2) 元素。这就是我们通常书写矩阵的形式,写成 A A A 32,3和2分别表示矩阵的第三行和第二列对应的元素,因此也就对应 6。
我也可以键入A(2,:) 来返回第二行的所有元素,冒号表示该行或该列的所有元素。
类似地,如果我键入 A(:,2),这将返回 A A A 矩阵第二列的所有元素,这将得到 2 4 6。
这表示返回 A A A 矩阵的第二列的所有元素。
你也可以在运算中使用这些较为复杂的索引。
我再给你展示几个例子,可能你也不会经常使用,但我还是输入给你看 A([1 3],:),这个命令意思是取 A A A 矩阵第一个索引值为1或3的元素,也就是说我取的是A矩阵的第一行和第三行的每一列,冒号表示的是取这两行的每一列元素,即:

可能这些比较复杂一点的索引操作你会经常用到。
我们还能做什么呢?依然是 A A A 矩阵,A(:,2) 命令返回第二列。
你也可以为它赋值,我可以取 A A A 矩阵的第二列,然后将它赋值为10 11 12,我实际上是取出了 A A A 的第二列,然后把一个列向量[10;11;12]赋给了它,因此现在 A A A 矩阵的第一列还是 1 3 5,第二列就被替换为 10 11 12。

接下来一个操作,让我们把 $A $设为A = [A, [100, 101,102]],这样做的结果是在原矩阵的右边附加了一个新的列矩阵,就是把 A A A矩阵设置为原来的 A A A 矩阵再在右边附上一个新添加的列矩阵。

最后,还有一个小技巧,如果你就输入 A(:),这是一个很特别的语法结构,意思是把 A A A中的所有元素放入一个单独的列向量,这样我们就得到了一个 9×1 的向量,这些元素都是 A A A 中的元素排列起来的。
再来几个例子:
我还是把 A 重新设为 [1 2; 3 4; 5 6],我再设一个 B B B为[11 12; 13 14; 15 16],我可以新建一个矩阵 C C C,C = [A B],这个意思就是把这两个矩阵直接连在一起,矩阵 A A A 在左边,矩阵 B B B 在右边,这样组成了 C C C矩阵,就是直接把 A A A和 B B B 合起来。

我还可以设C = [A; B],这里的分号表示把分号后面的东西放到下面。所以,[A;B]的作用依然还是把两个矩阵放在一起,只不过现在是上下排列,所以现在 A A A 在上面 B B B在下面, C C C 就是一个 6×2 矩阵。

简单地说,分号的意思就是换到下一行,所以 C 就包括上面的A,然后换行到下面,然后在下面放上一个 B B B。
另外顺便说一下,这个[A B]命令跟 [A, B] 是一样的,这两种写法的结果是相同的。
通过以上这些操作,希望你现在掌握了怎样构建矩阵,也希望我展示的这些命令能让你很快地学会怎样把矩阵放到一起,怎样取出矩阵,并且把它们放到一起,组成更大的矩阵。
3、计算数据
现在快速地初始化一些变量。比如设置 A A A为一个3×2的矩阵,设置 B B B为一个3 ×2矩阵,设置 C C C为2 × 2矩阵。
我想算两个矩阵的乘积,比如说 A × C A × C A×C,我只需键入A×C,这是一个 3×2 矩阵乘以 2×2矩阵,得到这样一个3×2矩阵。
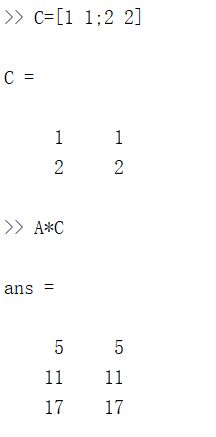
你也可以对每一个元素,做运算 方法是做点乘运算A.*B,这么做Octave将矩阵 A A A中的每一个元素与矩阵 B B B 中的对应元素相乘:A.*B
这里第一个元素1乘以11得到11,第二个元素2乘以12得到24,这就是两个矩阵的元素位运算。通常来说,在matlab中点号一般用来表示元素位运算。

这里是一个矩阵 A A A,这里我输入A.^2,这将对矩阵 A A A中每一个元素平方。

我们设 V V V为 [1; 2; 3] 是列向量,你也可以输入1./V,得到每一个元素的倒数,所以这样一来,就会分别算出 1/1 1/2 1/3。
矩阵也可以这样操作,1./A 得到 A A A中每一个元素的倒数。
同样地,这里的点号还是表示对每一个元素进行操作。
我们还可以进行求对数运算,也就是对每个元素进行求对数运算。
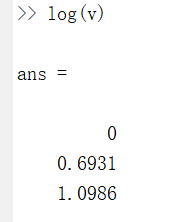
还有自然数 e e e的幂次运算,就是以 e e e为底,以这些元素为幂的运算。

我还可以用 abs来对 v v v 的每一个元素求绝对值,当然这里 v v v都是正数。我们换成另一个这样对每个元素求绝对值,得到的结果就是这些非负的元素。还有 – v –v –v,给出 v v v中每个元素的相反数,这等价于 -1 乘以 v v v,一般就直接用 − v -v −v
就好了,其实就等于 − 1 ∗ v -1*v −1∗v。

%百分号表示注释
还有一个技巧,比如说我们想对 v v v中的每个元素都加1,那么我们可以这么做,首先构造一个3行1列的1向量,然后把这个1向量跟原来的向量相加,因此 v v v向量从[1 2 3] 增至 [2 3 4]。我用了一个,length(v)命令,因此这样一来,ones(length(v) ,1) 就相当于ones(3,1),然后我做的是v +ones(3,1),也就是将 v v v 的各元素都加上这些1,这样就将 v v v 的每个元素增加了1。
另一种更简单的方法是直接用 v+1,v + 1 也就等于把 v v v 中的每一个元素都加上1。

矩阵 A A A 如果你想要求它的转置,那么方法是用A’,将得出 A 的转置矩阵。当然,如果我写(A')',也就是 A A A 转置两次,那么我又重新得到矩阵 A A A。
还有一些有用的函数,比如: a=[1 15 2 0.5],这是一个1行4列矩阵,val=max(a),这将返回 A A A矩阵中的最大值15。
我还可以写 [val, ind] =max(a),这将返回 A A A矩阵中的最大值存入 v a l val val,以及该值对应的索引,元素15对应的索引值为2,存入 i n d ind ind,所以 i n d = 2 ind =2 ind=2。
特别注意一下,如果你用命令 max(A), A A A是一个矩阵的话,这样做就是对每一列求最大值。
我们还是用这个例子,这个 a a a 矩阵a=[1 15 2 0.5],如果输入a<3,这将进行逐元素的运算,所以元素小于3的返回1,否则返回0。

因此,返回[1 1 0 1]。也就是说,对 a a a矩阵的每一个元素与3进行比较,然后根据每一个元素与3的大小关系,返回1和0表示真与假。
如果我写 find(a<3),这将告诉我 a a a 中的哪些元素是小于3的。
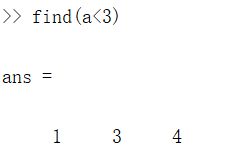
设A = magic(3),magic 函数将返回一个矩阵,称为魔方阵或幻方 (magic squares),它们具有以下这样的数学性质:它们所有的行和列和对角线加起来都等于相同的值。
当然据我所知,这在机器学习里基本用不上,但我可以用这个方法很方便地生成一个3行3列的矩阵,而这个魔方矩阵这神奇的方形屏幕。每一行、每一列、每一个对角线三个数字加起来都是等于同一个数。

在其他有用的机器学习应用中,这个矩阵其实没多大作用。
如果我输入 [r,c] = find(A>=7),这将找出所有 A A A矩阵中大于等于7的元素,因此, r r r 和 c c c分别表示行和列,这就表示,第一行第一列的元素大于等于7,第三行第二列的元素大于等于7,第二行第三列的元素大于等于7。

顺便说一句,其实我从来都不去刻意记住这个 find 函数,到底是怎么用的,我只需要会用help函数就可以了,每当我在使用这个函数,忘记怎么用的时候,我就可以用 help函数,键入 help find 来找到帮助文档。
最后再讲两个内容,一个是求和函数,这是 a a a 矩阵:

键入 sum(a),就把 a 中所有元素加起来了。
如果我想把它们都乘起来,键入 prod(a),prod 意思是product(乘积),它将返回这四个元素的乘积。
floor(a) 是向下四舍五入,因此对于 a a a 中的元素0.5将被下舍入变成0。

还有 ceil(a),表示向上四舍五入,所以0.5将上舍入变为最接近的整数,也就是1。
如果键入 max(rand(3),rand(3)),这样做的结果是返回两个3×3的随机矩阵,并且逐元素比较取最大值。
假如我输入max(A,[],1),这样做会得到每一列的最大值。
所以第一列的最大值就是8,第二列是9,第三列的最大值是7,这里的1表示取A矩阵第一个维度的最大值。
相对地,如果我键入max(A,[],2),这将得到每一行的最大值,所以,第一行的最大值是等于8,第二行最大值是7,第三行是9。

所以你可以用这个方法来求得每一行或每一列的最值,另外,你要知道,默认情况下max(A)返回的是每一列的最大值,如果你想要找出整个矩阵A的最大值,你可以输入max(max(A)),或者你可以将 A A A 矩阵转成一个向量,然后键入 max(A(:)),这样做就是把 A A A 当做一个向量,并返回 A A A向量中的最大值。
最后,让我们把 A A A设为一个9行9列的魔方阵,魔方阵具有的特性是每行每列和对角线的求和都是相等的。
这是一个9×9的魔方阵,我们来求一个 sum(A,1),这样就得到每一列的总和,这也验证了一个9×9的魔方阵确实每一列加起来都相等,都为369。
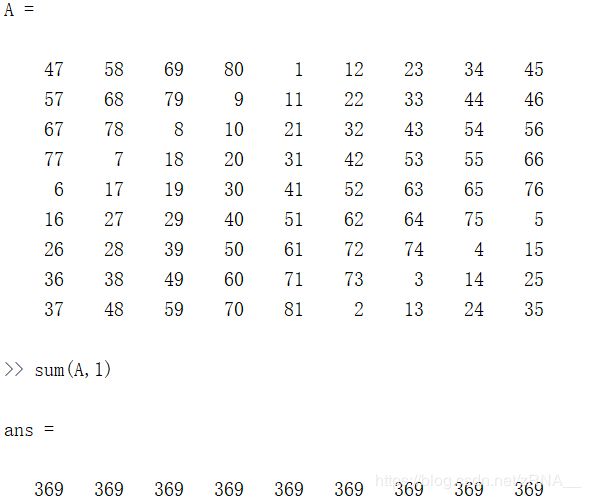
现在我们来求每一行的和,键入sum(A,2),这样就得到了 A A A 中每一行的和加起来还是369。
现在我们来算$A $的对角线元素的和。我们现在构造一个9×9 的单位矩阵,键入 eye(9),
然后我们要用 A A A逐点乘以这个单位矩阵,除了对角线元素外,其他元素都会得到0。
键入sum(sum(A.*eye(9))
这实际上是求得了,这个矩阵对角线元素的和确实是369。
你也可以求另一条对角线的和也是是369。
flipup/flipud 表示向上/向下翻转。
同样地,如果你想求这个矩阵的逆矩阵,键入pinv(A),通常称为伪逆矩阵,你就把它看成是矩阵 A A A 求逆,因此这就是 A A A矩阵的逆矩阵。
设 temp = pinv(A),然后再用 t e m p temp temp 乘以 A A A,这实际上得到的就是单位矩阵,对角线为1,其他元素为0。
如何对矩阵中的数字进行各种操作,在运行完某个学习算法之后,通常一件最有用的事情是看看你的结果,或者说让你的结果可视化,在接下来的视频中,我会非常迅速地告诉你,如何很快地画图,如何只用一两行代码,你就可以快速地可视化你的数据,这样你就能更好地理解你使用的学习算法。
4、绘图数据
参考视频: 5 - 4 - Plotting Data (10 min).mkv
当开发学习算法时,往往几个简单的图,可以让你更好地理解算法的内容,并且可以完整地检查下算法是否正常运行,是否达到了算法的目的。
例如在之前的视频中,我谈到了绘制成本函数 J ( θ ) J(\theta) J(θ),可以帮助确认梯度下降算法是否收敛。通常情况下,绘制数据或学习算法所有输出,也会启发你如何改进你的学习算法。幸运的是,matlab有非常简单的工具用来生成大量不同的图。当我用学习算法时,我发现绘制数据、绘制学习算法等,往往是我获得想法来改进算法的重要部分。在这段视频中,我想告诉你一些matlab的工具来绘制和可视化你的数据。
我们先来快速生成一些数据用来绘图。

如果我想绘制正弦函数,这是很容易的,我只需要输入plot(t,y1),并回车,就出现了这个图:
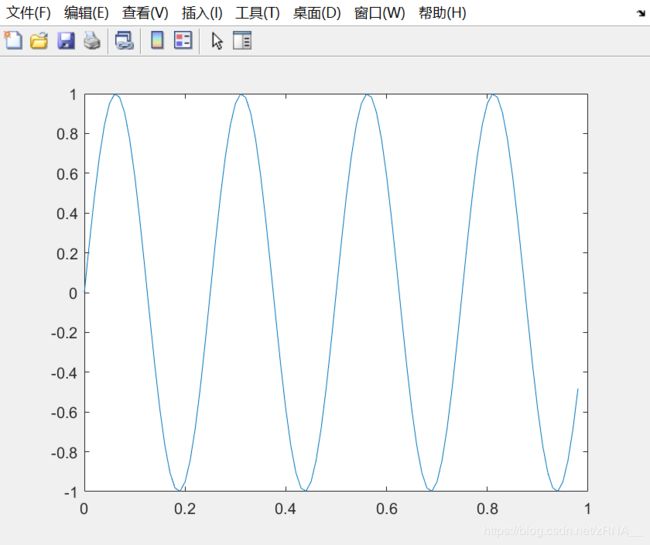
横轴是 t t t变量,纵轴是 y 1 y1 y1,也就是我们刚刚所输出的正弦函数。
让我们设置 y 2 y2 y2
![]()
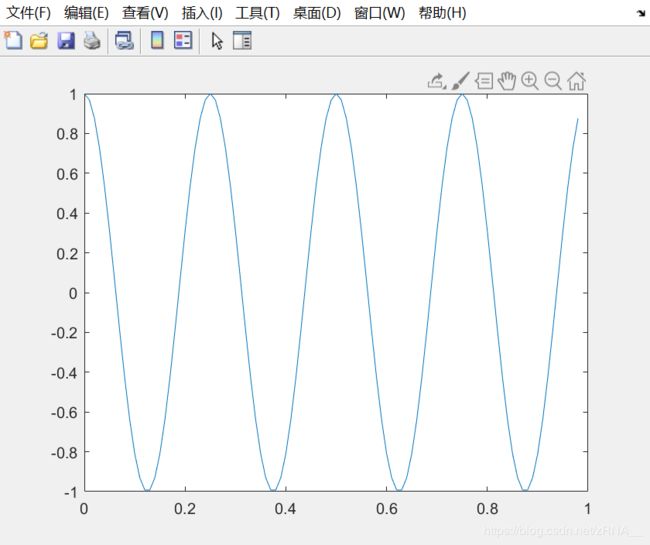
将会消除之前的正弦图,并且用这个余弦图来代替它,这里纵轴 c o s ( x ) cos(x) cos(x)从1开始,
如果我要同时表示正弦和余弦曲线。
我要做的就是,输入:plot(t, y1),得到正弦函数,我使用函数hold on,hold on函数的功能是将新的图像绘制在旧的之上。
我现在绘制 y 2 y2 y2,输入:plot(t, y2)。
我要以不同的颜色绘制余弦函数,所以我在这里输入带引号的r绘制余弦函数, r r r表示所使用的颜色:plot(t,y2,’r’),再加上命令xlabel('time'),
来标记X轴即水平轴,输入ylabel('value'),来标记垂直轴的值。
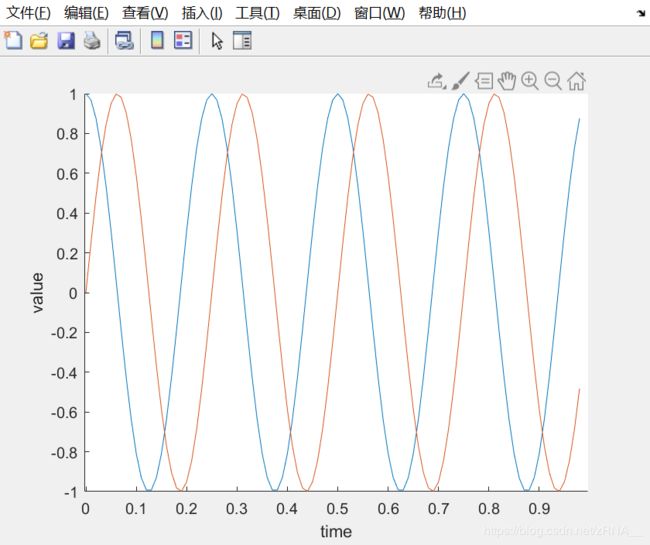
同时我也可以来标记我的两条函数曲线,用这个命令 legend('sin','cos')将这个图例放在右上方,表示这两条曲线表示的内容。最后输入title('myplot'),在图像的顶部显示这幅图的标题。

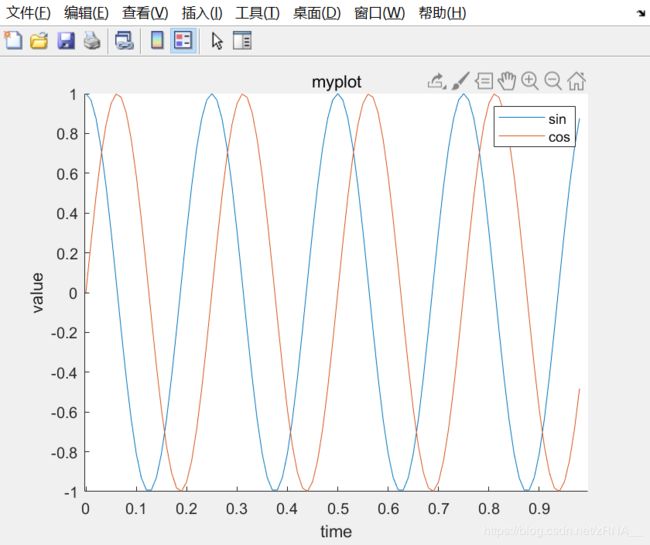
如果你想保存这幅图像,你输入print –dpng 'myplot.png',png是一个图像文件格式,如果你这样做了,它可以让你保存为一个文件。
也可以保存为很多其他的格式,你可以键入help plot。
最后如果你想,删掉这个图像,用命令close会让这个图像关掉。
也可以让你为图像标号
你键入figure(1); plot(t, y1);将显示第一张图,绘制了变量 t t t y 1 y1 y1。
键入figure(2); plot(t, y2); 将显示第一张图,绘制了变量 t t t y 2 y2 y2。
subplot命令,我们要使用subplot(1,2,1),它将图像分为一个1*2的格子,也就是前两个参数,然后它使用第一个格子,也就是最后一个参数1的意思。

我现在使用第一个格子,如果键入plot(t,y1),现在这个图显示在第一个格子。如果我键入subplot(1,2,2),那么我就要使用第二个格子,键入plot(t,y2);现在y2显示在右边,也就是第二个格子。
最后一个命令,你可以改变轴的刻度,比如改成[0.5 1 -1 1],输入命令:axis([0.5 1 -1 1])也就是设置了右边图的 x x x轴和 y y y轴的范围。具体而言,它将右图中的横轴的范围调整至0.5到1,竖轴的范围为-1到1。

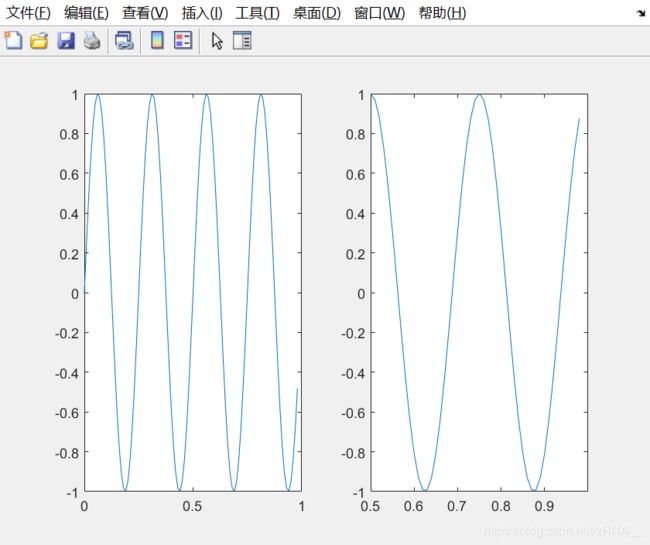
你不需要记住所有这些命令,如果你需要改变坐标轴,或者需要知道axis命令,你可以用matlab中用help命令了解细节。
最后,还有几个命令。
Clf(清除一幅图像)。
让我们设置A等于一个5×5的magic方阵:
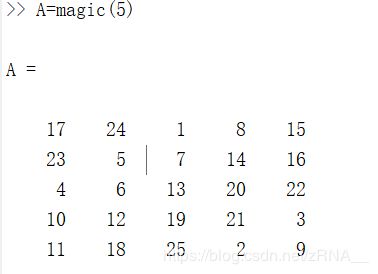
有时用一个巧妙的方法来可视化矩阵,也就是imagesc(A)命令,它将会绘制一个5*5的矩阵,一个5*5的彩色格图,不同的颜色对应A矩阵中的不同值。
还可以使用函数colorbar,让我用一个更复杂的命令 imagesc(A),colorbar,colormap gray。这实际上是在同一时间运行三个命令:运行imagesc,然后运行,colorbar,然后运行colormap gray。
它生成了一个颜色图像,一个灰度分布图,并在右边也加入一个颜色条。所以这个颜色条显示不同深浅的颜色所对应的值。
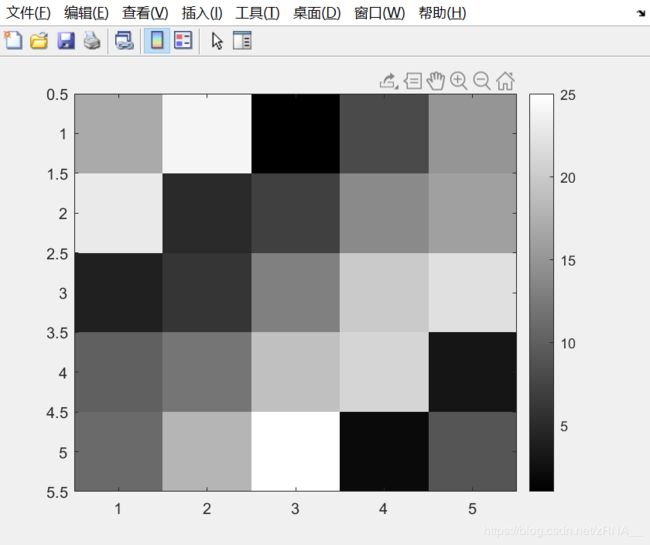
你可以看到在不同的方格,它对应于一个不同的灰度。
输入`你可以看到在不同的方格,它对应于一个不同的灰度。
输入`imagesc(magic(15)),colorbar,colormap gray``
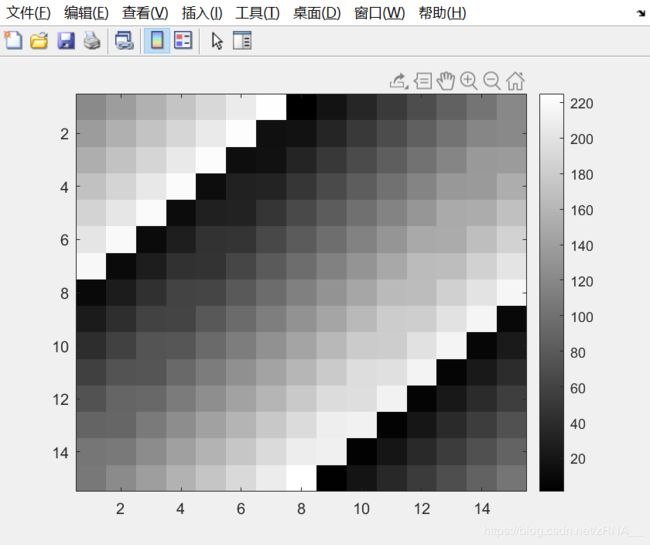
这将会是一幅15*15的magic方阵值的图。
最后,总结一下这段视频。你看到我所做的是使用逗号连接函数调用。如果我键入 a = 1 a=1 a=1, b = 2 b=2 b=2, c = 3 c=3 c=3然后按Enter键,其实这是将这三个命令同时执行,或者是将三个命令一个接一个执行,它将输出所有这三个结果。
这很像 a = 1 a=1 a=1; b = 2 b=2 b=2; c = 3 c=3 c=3;如果我用分号来代替逗号,则没有输出出任何东西。
这里我们称之为逗号连接的命令或函数调用。

用逗号连接是另一种matlab中更便捷的方式,将多条命令例如imagesc colorbar colormap,将这多条命令写在同一行中。
5、控制语句:for,while,if语句
参考视频: 5 - 5 - Control Statements_ for, while, if statements (13 min).mkv
在这段视频中,我想告诉你怎样为你的 Octave 程序写控制语句。诸如:“for” “while” “if” 这些语句,并且如何定义和使用方程。
如何使用 “for” 循环。
首先,要将 v v v 值设为一个10行1列的零向量。
接着我要写一个 “for" 循环,让 i i i 等于 1 到 10,写出来就是 i = 1:10。我要设$ v(i)$的值等于 2 的 i i i 次方,循环最后写上“end”。
向量 v v v 的值就是这样一个集合 2的一次方、2的二次方,依此类推。这就是我的 i i i 等于 1 到 10的语句结构,让 i i i 遍历 1 到 10的值。


另外,你还可以通过设置你的 indices (索引) 等于 1一直到10,来做到这一点。这时indices 就是一个从1到10的序列。
你也可以写 i = indices,这实际上和我直接把 i 写到 1 到 10 是一样。你可以写 disp(i),也能得到一样的结果。所以 这就是一个 “for” 循环。

如果你对 “break” 和 “continue” 语句比较熟悉,Octave里也有 “break” 和 “continue”语句,你也可以在 Octave环境里使用那些循环语句。
但是首先让我告诉你一个 while 循环是如何工作的:

这是什么意思呢:我让 i i i 取值从 1 开始,然后我要让 v ( i ) v(i) v(i) 等于 100,再让 i i i 递增 1,直到 i i i 大于 5停止。
现在来看一下结果,我现在已经取出了向量的前五个元素,把他们用100覆盖掉,这就是一个while循环的句法结构。
现在我们来分析另外一个例子:

这里我将向你展示如何使用break语句。比方说 v(i) = 999,然后让 i = i+1,当 i i i 等于6的时候 break (停止循环),结束 (end)。
当然这也是我们第一次使用一个 if 语句,所以我希望你们可以理解这个逻辑,让 i i i 等于1 然后开始下面的增量循环,while语句重复设置 v ( i ) v(i) v(i) 等于999,不断让 i i i增加,然后当 i i i 达到6,做一个中止循环的命令,尽管有while循环,语句也就此中止。所以最后的结果是取出向量 v v v 的前5个元素,并且把它们设置为999。
所以,这就是if 语句和 while 语句的句法结构。并且要注意要有end,上面的例子里第一个 end 结束的是 if
语句,第二个 end 结束的是 while 语句。
现在让我告诉你使用 if-else 语句:

最后,让我们来说说函数 (functions),如何定义和调用函数。
我在桌面上存了一个预先定义的文件名为 “squarethisnumber.m”,这就是在 matlab 环境下定义的函数。
让我们打开这个文件。请注意,我使用的是微软的写字板程序来打开这个文件,我只是想建议你,如果你也使用微软的Windows系统,那么可以使用写字板程序,而不是记事本来打开这些文件。如果你有别的什么文本编辑器也可以,记事本有时会把代码的间距弄得很乱。如果你只有记事本程序,那也能用。我建议你用写字板或者其他可以编辑函数的文本编辑器。
现在我们来说如何在 matlab 里定义函数:
这个文件只有三行:
第一行写着 function y = squareThisNumber(x),这就告诉 matlab,我想返回一个 y值,我想返回一个值,并且返回的这个值将被存放于变量 y y y 里。另外,它告诉了Octave这个函数有一个参数,就是参数 x x x,还有定义的函数体,也就是 y y y 等于 x x x 的平方。
还有一个其他许多编程语言都没有的概念,那就是它可以允许你定义一个函数,使得返回值是多个值或多个参数。这里就是一个例子,定义一个函数叫:
“SquareAndCubeThisNumber(x)” ( x x x的平方以及 x x x的立方)
这说的就是函数返回值是两个: y 1 y1 y1 和 y 2 y2 y2,接下来就是 y 1 y1 y1是被平方后的结果, y 2 y2 y2是被立方后的结果,这就是说,函数会真的返回2个值。
有些同学可能会根据你使用的编程语言,比如你们可能熟悉的C或C++,通常情况下,认为作为函数返回值只能是一个值,但matlab 的语法结构就不一样,可以返回多个值。
如果我键入 [a,b] = SquareAndCubeThisNumber(5),然后, a a a就等于25, b b b 就等于5的立方125。
所以说如果你需要定义一个函数并且返回多个值,这一点常常会带来很多方便。
最后,我来给大家演示一下一个更复杂一点的函数的例子。
比方说,我有一个数据集,像这样,数据点为[1,1], [2,2],[3,3],我想做的事是定义一个 matlab 函数来计算代价函数 J ( θ ) J(\theta) J(θ),就是计算不同 θ \theta θ值所对应的代价函数值 J J J。
首先让我们把数据放到 matlab 里,我把我的矩阵设置为X = [1 1; 1 2; 1 3];
请仔细看一下这个函数的定义,确保你明白了定义中的每一步。

我键入 J = costFunctionJ (X, y, theta),它就计算出 J J J等于0,这是因为如果我的数据集 x x x 为 [1;2;3], y y y 也为 [1;2;3] 然后设置 θ 0 \theta_0 θ0 等于0, θ 1 \theta_1 θ1等于1,这给了我恰好45度的斜线,这条线是可以完美拟合我的数据集的。

而相反地,如果我设置 θ \theta θ 等于[0;0],那么这个假设就是0是所有的预测值,和刚才一样,设置 θ 0 \theta_0 θ0 = 0, θ 1 \theta_1 θ1也等于0,然后我计算的代价函数,结果是2.333。实际上,他就等于1的平方,也就是第一个样本的平方误差,加上2的平方,加上3的平方,然后除以 2 m 2m 2m,也就是训练样本数的两倍,这就是2.33。

因此这也反过来验证了我们这里的函数,计算出了正确的代价函数。这些就是我们用简单的训练样本尝试的几次试验,这也可以作为我们对定义的代价函数 J J J进行了完整性检查。确实是可以计算出正确的代价函数的。至少基于这里的 x x x和 y y y是成立的。也就是我们这几个简单的训练集,至少是成立的。
6、向量化
参考视频: 5 - 6 - Vectorization (14 min).mkv
在这段视频中,我将介绍有关向量化的内容,无论你是用MATLAB,还是别的语言,比如Octave或者你正在用Python、NumPy 或 Java C C++,所有这些语言都具有各种线性代数库,这些库文件都是内置的,容易阅读和获取,他们通常写得很好,已经经过高度优化,通常是数值计算方面的博士或者专业人士开发的。
而当你实现机器学习算法时,如果你能好好利用这些线性代数库,或者数值线性代数库,并联合调用它们,而不是自己去做那些函数库可以做的事情。如果是这样的话,那么通常你会发现:首先,这样更有效,也就是说运行速度更快,并且更好地利用你的计算机里可能有的一些并行硬件系统等等;其次,这也意味着你可以用更少的代码来实现你需要的功能。因此,实现的方式更简单,代码出现问题的有可能性也就越小。
举个具体的例子:与其自己写代码做矩阵乘法。如果你只在matlab中输入 a a a乘以 b b b就是一个非常有效的两个矩阵相乘的程序。有很多例子可以说明,如果你用合适的向量化方法来实现,你就会有一个简单得多,也有效得多的代码。
让我们来看一些例子:这是一个常见的线性回归假设函数: h θ ( x ) = ∑ j = 0 n θ j x j {{h}_{\theta }}(x)=\sum\limits_{j=0}^{n}{{{\theta }_{j}}{{x}_{j}}} hθ(x)=j=0∑nθjxj
如果你想要计算 h θ ( x ) h_\theta(x) hθ(x) ,注意到右边是求和,那么你可以自己计算 j = 0 j = 0 j=0 到$ j = n$ 的和。但换另一种方式来想想,把 h θ ( x ) h_\theta(x) hθ(x) 看作 θ T x \theta^Tx θTx,那么你就可以写成两个向量的内积,其中 θ \theta θ就是 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2,如果你有两个特征量,如果 n = 2 n = 2 n=2,并且如果你把 x x x 看作 x 0 x_0 x0、 x 1 x_1 x1、 x 2 x_2 x2,这两种思考角度,会给你两种不同的实现方式。
比如说,这是未向量化的代码实现方式:

计算 h θ ( x ) h_\theta(x) hθ(x)是未向量化的,我们可能首先要初始化变量 p r e d i c t i o n prediction prediction 的值为0.0,而这个变量 p r e d i c t i o n prediction prediction 的最终结果就是 h θ ( x ) h_\theta(x) hθ(x),然后我要用一个 for 循环, j j j 取值 0 到 n + 1 n+1 n+1,变量 p r e d i c t i o n prediction prediction 每次就通过自身加上$ theta(j) $乘以 x ( j ) x(j) x(j)更新值,这个就是算法的代码实现。
顺便我要提醒一下,这里的向量我用的下标是0,所以我有 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2,但因为MATLAB的下标从1开始,在 MATLAB 中 θ 0 \theta_0 θ0,我们可能会用 t h e t a ( 1 ) theta(1) theta(1) 来表示,这第二个元素最后就会变成, t h e t a ( 2 theta(2 theta(2) 而第三个元素,最终可能就用 t h e t a ( 3 ) theta(3) theta(3)表示,因为MATLAB中的下标从1开始,这就是为什么这里我的 for 循环, j j j取值从 1 直到 n + 1 n+1 n+1,而不是从 0 到 n n n。这是一个未向量化的代码实现方式,我们用一个 for 循环对 n n n 个元素进行加和。
作为比较,接下来是向量化的代码实现:

你把x和 θ \theta θ看做向量,而你只需要令变量 p r e d i c t i o n prediction prediction等于 t h e t a theta theta转置乘以 x x x,你就可以这样计算。与其写所有这些for循环的代码,你只需要一行代码,这行代码就是利用 matlab 的高度优化的数值,线性代数算法来计算两个向量 θ \theta θ以及 x x x的内积,这样向量化的实现更简单,它运行起来也将更加高效。这就是 matlab 所做的而向量化的方法,在其他编程语言中同样可以实现。
让我们来看一个C++ 的例子:

与此相反,使用较好的**C++数值线性代数库,你可以写出像右边这样的代码,因此取决于你的数值线性代数库的内容。你只需要在C++**中将两个向量相乘,根据你所使用的数值和线性代数库的使用细节的不同,你最终使用的代码表达方式可能会有些许不同,但是通过一个库来做内积,你可以得到一段更简单、更有效的代码。
现在,让我们来看一个更为复杂的例子,这是线性回归算法梯度下降的更新规则:
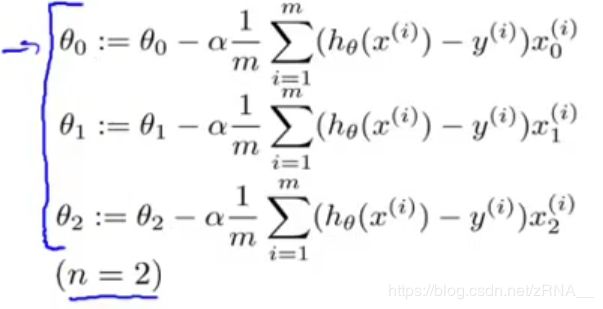
我们用这条规则对$ j$ 等于 0、1、2等等的所有值,更新对象 θ j \theta_j θj,我只是用 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2来写方程,假设我们有两个特征量,所以 n n n等于2,这些都是我们需要对 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2进行更新,这些都应该是同步更新,我们用一个向量化的代码实现,这里是和之前相同的三个方程,只不过写得小一点而已。
你可以想象实现这三个方程的方式之一,就是用一个 for 循环,就是让 j j j等于0、等于1、等于2,来更新 θ j \theta_j θj。但让我们用向量化的方式来实现,看看我们是否能够有一个更简单的方法。基本上用三行代码或者一个for 循环,一次实现这三个方程。让我们来看看怎样能用这三步,并将它们压缩成一行向量化的代码来实现。做法如下:
我打算把 θ \theta θ看做一个向量,然后我用 θ \theta θ- α \alpha α 乘以某个别的向量 δ \delta δ 来更新 θ \theta θ。
这里的 δ \delta δ 等于
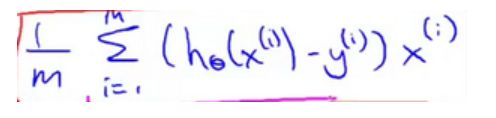
解释一下是怎么回事:我要把 θ \theta θ看作一个向量,有一个 n + 1 n+1 n+1 维向量, α \alpha α 是一个实数, δ \delta δ在这里是一个向量。

所以这个减法运算是一个向量减法,因为 α \alpha α 乘以 δ是一个向量,所以 θ \theta θ就是 θ \theta θ - α δ \alpha \delta αδ得到的向量。
那么什么是向量 δ \delta δ 呢 ?
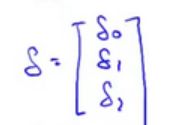
X ( i ) X^{(i)} X(i)是一个向量
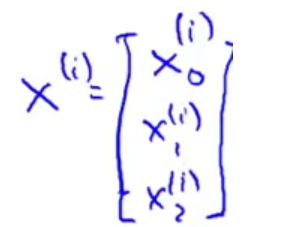
你就会得到这些不同的式子,然后作加和。
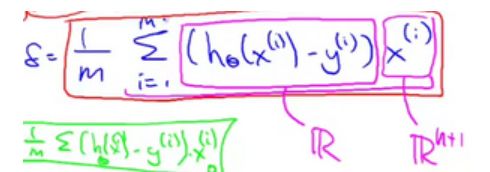
实际上,在以前的一个小测验,如果你要解这个方程,我们说过为了向量化这段代码,我们会令u = 2v +5w因此,我们说向量 u u u等于2乘以向量 v v v加上5乘以向量 w w w。用这个例子说明,如何对不同的向量进行相加,这里的求和是同样的道理。
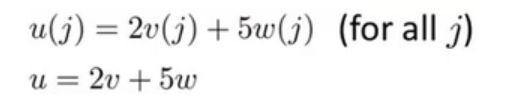
这就是为什么我们能够向量化地实现线性回归。
所以,我希望步骤是有逻辑的。请务必看视频,并且保证你确实能理解它。如果你实在不能理解它们数学上等价的原因,你就直接实现这个算法,也是能得到正确答案的。所以即使你没有完全理解为何是等价的,如果只是实现这种算法,你仍然能实现线性回归算法。如果你能弄清楚为什么这两个步骤是等价的,那我希望你可以对向量化有一个更好的理解,如果你在实现线性回归的时候,使用一个或两个以上的特征量。
有时我们使用几十或几百个特征量来计算线性归回,当你使用向量化地实现线性回归,通常运行速度就会比你以前用你的for循环快的多,也就是自己写代码更新 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2。
因此使用向量化实现方式,你应该是能够得到一个高效得多的线性回归算法。而当你向量化我们将在之后的课程里面学到的算法,这会是一个很好的技巧,无论是对于matlab 或者一些其他的语言 如C++、Java 来让你的代码运行得更高效。