以LeNet-5为例理解CNN
在用caffe实现对MNIST手写数字分类的过程中发现利用的网络是LetNet-5.决定从这个网络入手好好认识一下CNN。
LeNet-5早在1998年就出现了(5表示5层模型),标志着CNN的诞生。以其作者YannLeCun的名字命名。但是却没有得到广泛的应用,原因一个是对机器要求高(当时没有GPU),一个是因为其他算法(SVM,老实说是你干的吧?)也能达到类似的效果甚至超过。之后的模型还有AlexNet(以人的名字命名)、VGG(以机构名命名)、GoogleNet(机构名命名)、ResNet(以核心算法命名)。既然都是千年的狐狸(神经网络),比的就是谁的模型更好,可以更好地模拟人脑认知的过程。而之后出现的R-CNN(使用了AlexNet),Fast R-CNN等就好比是《聊斋》,是一套方法,重要的是把故事讲好。看《聊斋》的书,哪只狐狸什么样子当然无所谓;但是如果是看电影,那么扮演狐狸的演员,她对狐狸的把握、还原就至关重要了。至于Caffe、TensorFlow、Torch等深度学习框架,仅仅是一个工具,就像是写作的笔,没有马良的笔那么神奇,但也都足够我们用来书写自己的故事。
胡乱比喻了一下,不至于把他们混淆。下来好好认识一下这个LeNet-5网络及CNN。
我准备从三个角度介绍一下LeNet-5网络。先是侧重每部分的作用,整体把握一下网络的思路。然后从连接的角度,层与层之间在数学上的关系。最后对CNN中特有的几个概念做一下解读。
一
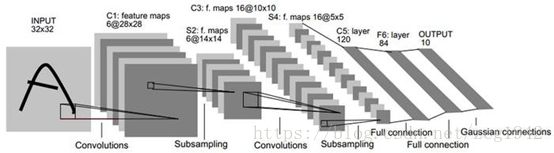
既然说是5层网络,那么我们看一看到底是哪5层。看来看去,发现是7层(算上输出层,不算输入层)。就拿论文中的插图来看,上图的顶部是每层的名字。看来作者认为是6层。。
INPUT,输入图像是32x32,对比之下,MNIST输入的图像是28x28的。
C1:C意味着这是一个卷积层。在这一层我们将得到feature map。卷积应该不是一个陌生的概念,在图像处理中,简单来说就是旋转180度之后卷积核和图像对应像素加权求和。卷积之后的图像是一个“响应”,如果是边缘检测算子,那么得到的响应就是图像的边缘,现在我们只知道我们希望得到的响应是feature map,得到输入图像的特征,但是不知道的是卷积核的参数(权重),所以我们需要一个网络来训练它。
这一层卷积核的大小是5x5.卷积核滑动一行之后,得到的结果的边长变为32-5+1,得到的feature map大小是28x28.有6个不同的卷积核,希望从不同的角度得到图像的特征。所以待定参数是(5x5+1)*6=156。刚才讲到,参数要由网络求得,网络的层与层之间是通过feature map连接的。得到的28x28的feature map的每一个像素对应5x5+1个权值,这有点像MIMO,所以这里的连接个数是28x28x156=122304个。
S2:S指的是Subsamples,这层经过下采样得到的也是featuremap。下采样的作用是减少计算量,同时保留有用的信息。但是这里的下采样和普通的不一样,不是插值的方法,而是用一种叫池化的方法。就是把一幅图像分割成几个块,每个块的输出是这个块原有像素的统计结果,可以是最大值,那就是最大值池化Max_pooling,如果是均值,那就是均值池化Mean_Pooling。
这一层池的大小是2x2.所以最后得到6个14x14的feature map。和卷积层的连接数的计算方法一样,连接数=参数个数*feature map大小=(2x2+1)x6x14x14=5880
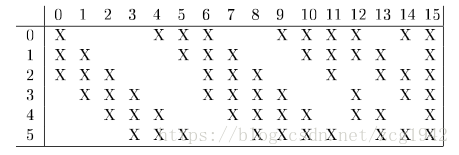
C3:这一层还是卷积层。卷积核大小还是5x5.但是有16个(14-5+1)x(14-5+1)=10x10的fea map。所以得到16个这个层除了要对下采样得到的feature map再进行一次卷积,还有一个问题值得注意。既然有16个卷积核,那么对每一幅feature map就可以得到16个全新的,总共可以得到16x6个feature map,但是这里得到的正好是16个feature map,所以其实在卷积之前,对池化后的feature map进行了组合,得到了16个新的图像,每个图像对应一个特有的卷积核,最终得到16个f.map。所以,现在的问题就是如何对6个feature map排列组合得到16个新图像。论文中给出了一种组合方式(部分连接):
一共6行10列,每列的X表示C3中的一个feature map与S2中的feature map的连接情况。可以看到C3一共有6个与3个S2中的feature map连接,有9个是4连接,有一个是全连接。参数数目:(5x5x3+1)x6+(5x5x4+1)x9+5x5x6+1=1516.这里得到的每一个feature map其实是多核多通道卷积。把每一列叫作一个卷积核,它由若干个卷积模板构成。因为是多个卷积核模板卷积的结果得到一个feature map,仍然认为是一个卷积核,所以每列只有一个偏置参数。所以连接的数目=1516x10x10=151600.
S4:也是下采样层,得到16个5x5的feature map。连接数=(2x2+1)x5x5x16=2000.
C5:又一个卷积层。注意到它与S4是Fullconnection,因为卷积核大小依然是5x5,正好与S4得到的feature map大小一样,得到的feature map就是1x1大小的,时刻注意连接指的是feature map之间的连接。还注意到这里的示意图是带状了,这是因为feature map到这里太多了,有多少呢?有120个。如果用类似上图的矩阵表示,那就是16x120的全1矩阵。
F6:只有86个神经元,继续降低特征的维数。采用了正切函数。连接数=86x(120+1)=10164.
完全连接层就是传统的多层感知机。使用softmax连接函数,输出的概率和为1.
最终经过高斯连接,得到10维的输出。输出层采用了RBF径向欧式距离函数。计算输入向量和参数向量的欧式距离。
卷积神经网络在本质上是一种输入到输出的映射,它能够学习大量的输入与输出之间的映射关系,而不需要任何输入与输出之间的精确的数学表达式,只要用已知的模式对卷积神经网络加以训练,网络就具有输入与输出之间的映射能力。卷积网络是有监督学习,所以它的样本集都形如:(输入向量,理想输出向量)之类的向量对构成。
在训练之前,所有权值都用一些不同的小随机数进行初始化,小的随机数可以保证网络不会因权值太大而进入饱和状态,从而导致训练失败。不同则保证网络可以正常学习。
如果要是用相同的数去初始化矩阵,网络会没有学习的能力。
关于偏置和激活
卷积、池化其实不是简单的加权求和、统计最大值/均值。首先,它们都会加一个偏置系数。池化的连接处还有一个激活函数,这同样是模仿人的神经系统,因为刺激达到一定程度神经元才会做出反应,而反应又可分为刺激(正)和抑制(负)。激活函数的选取也很重要,可选择的有sigmoid函数、tanh双曲正切函数、ReLU函数。前两个函数是饱和的。现在一般使用ReLu作为激活函数(虽然sigmoid的求导形式优美,f’(x)=f(x)(1-f(x)),可以加速收敛。
参考6提到卷积之后也会加ReLU函数。ReLU 是一个针对元素的操作(应用于每个像素),并将特征映射中的所有负像素值替换为零。ReLU 的目的是在卷积神经网络中引入非线性因素,因为在实际生活中我们想要用神经网络学习的数据大多数都是非线性的(卷积是一个线性运算)
关于C3的部分连接
C3中的每一个Feature Map连接到S2的所有6个Feature Map或者是几个Feature Map。表示本层的Feature Map是上一层提取的Feature Map的不同组合。为什么不把S2的每一个Feature Map连接到S3的每一个Feature Map中?原因有2: 第一,不完全连接机制连接的数量保持在合理范围,第二,这样破坏了网络的对称性,由于不同的Feature Map有不同的输入,所以迫使他们抽取不同的特征(理想状态特征互补)。
关于连接数的计算
上文中提到连接数=参数个数*featuremap大小,但是以C2为例,不同的feature map是由不同的卷积核得到的,所以有一些连接对是没有联系的。为什么也要将他们连接起来呢?我的思考是虽然他们没有因果关系,但是因为我们的目的是在构建网络之后训练得到网络的参数,所以除了前向传播通过损失函数得到损失,我们还需要向后传播梯度信息,更新权重。反向传播的过程中,已经得到的某个feature map当然可以推算对应的卷积核,但是对其他的卷积核也有启示作用,因为我们是基于局部感知的,每个神经元只负责对图像某一部分,这里的某一部分,我觉得指的不是图像的空域部分,而是图像的某一种特征,如颜色或者边缘信息,然后在更高的层次进行组合得到全局的,更加完整的感知。这也解释了为什么C3部分连接组合,也可以解释为什么一开始选择用6个卷积核。
关于池化的作用
池化的作用是逐步减少输入的空间大小[4]。具体来说有以下四点:
使输入(特征维度)更小,更易于管理
减少网络中的参数和运算次数,因此可以控制过拟合 [4]
使网络对输入图像微小的变换、失真和平移更加稳健(输入图片小幅度的失真不会改池化的输出结果 —— 因为我们取了邻域的最大值/平均值)。
可以得到尺度几乎不变的图像(确切的术语是“等变”)。这是非常有用的,这样无论图片中的物体位于何处,我们都可以检测到,(详情参阅[18]和[19])
Reference:
1.1998论文:http://pdfs.semanticscholar.org/162d/958ff885f1462aeda91cd72582323fd6a1f4.pdf
2.SVM干的https://www.cnblogs.com/alexanderkun/p/6923064.html
3.https://blog.csdn.net/genius_zz/article/details/52804585
4.https://www.cnblogs.com/ranjiewen/articles/7467600.html
5.诺贝尔医学奖可视皮层是分级的https://www.cnblogs.com/alexcai/p/5506806.html
6.http://www.mamicode.com/info-detail-2310074.html