【OpenCV学习笔记】之仿射变换(Affine Transformation)
-
图像的几何变换——拉伸、收缩、扭曲、旋转(stretch,shrink,distortion,rotation)
拉伸、收缩、扭曲、旋转是图像的几何变换,在三维视觉技术中大量应用到这些变换,又分为仿射变换和透视变换。仿射变换通常用单应性(homography)建模,利用cvWarpAffine解决稠密仿射变换,用cvTransform解决稀疏仿射变换。仿射变换可以将矩形转换成平行四边形,它可以将矩形的边压扁但必须保持边是平行的,也可以将矩形旋转或者按比例变化。透视变换提供了更大的灵活性,一个透视变换可以将矩阵转变成梯形。当然,平行四边形也是梯形,所以仿射变换是透视变换的子集。
1、仿射变换(Affine transformation)
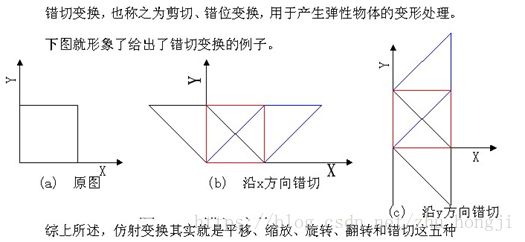
因此,空间变换中的仿射变换对应着五种变换,平移,缩放,旋转,翻转,错切。而这五种变化由原图像转变到变换图像的过程,可以用仿射变换矩阵进行描述。而这个变换过程可以用一个2*3的矩阵与原图进行相乘得到。
2、透视变换(Perspective transformation)
从原理可以得出,透视变换除了变换矩阵是一个3*3的矩阵和需要四个控点以外,透视变换在其他方面都和仿射变换完全类似。
3、 OpenCV里面API 的介绍
3.1 仿射变换
OpenCV通过两个函数的组合使用来实现仿射变换,也就是仿射变换的两步:
第一步:获取仿射映射矩阵(两种):
(1)getAffineTransform //三点法
Mat M1=getAffineTransform(const Point2f* src, const Point2f* dst)
//参数const Point2f* src:原图的三个固定顶点
//参数const Point2f* dst:目标图像的三个固定顶点
//返回值:Mat型变换矩阵,可直接用于warpAffine()函数
//注意,顶点数组长度超过3个,则会自动以前3个为变换顶点;数组可用Point2f[]或Point2f*表示
(2)getRotationMatrix2D //直接指定比例和角度
Mat M2=getRotationMatrix2D (CvPoint2D32f center,double angle,double scale)
//参数CvPoint2D32f center,表示源图像旋转中心
//参数double angle,旋转角度,正值表示逆时针旋转
//参数double scale,缩放系数
第二步:进行仿射变换
C++ void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())
//参数InputArray src:输入变换前图像
//参数OutputArray dst:输出变换后图像,需要初始化一个空矩阵用来保存结果,不用设定矩阵尺寸
//参数InputArray M:变换矩阵,用另一个函数getAffineTransform()计算
//参数Size dsize:设置输出图像大小
//参数int flags = INTER_LINEAR:设置插值方式,默认方式为线性插值(另一种WARP_FILL_OUTLIERS)
//参数int borderMode=BORDER_CONSTANT:边界像素模式,默认值BORDER_CONSTANT
//参数const Scalar& borderValue=Scalar(),在恒定边界情况下取的值,默认值为Scalar(),即0
第五个参数插值方式可选方式:
示例程序:
//仿射变换—平移,旋转,缩放,翻转,错切
#include "stdafx.h"
#include
#include
#include
using namespace cv;
using namespace std;
int main(int argc, char* argv) {
Mat src, dst;
src = imread("C:/Users/59235/Desktop/image/girl5.jpg");
if (!src.data) {
printf("could not load image...\n");
return -1;
}
namedWindow("original image", CV_WINDOW_AUTOSIZE);
imshow("original image", src);
Mat dst_warp, dst_warpRotateScale, dst_warpTransformation, dst_warpFlip;
Point2f srcPoints[3];//原图中的三点 ,一个包含三维点(x,y)的数组,其中x、y是浮点型数
Point2f dstPoints[3];//目标图中的三点
//第一种仿射变换的调用方式:三点法
//三个点对的值,上面也说了,只要知道你想要变换后图的三个点的坐标,就可以实现仿射变换
srcPoints[0] = Point2f(0, 0);
srcPoints[1] = Point2f(0, src.rows);
srcPoints[2] = Point2f(src.cols, 0);
//映射后的三个坐标值
dstPoints[0] = Point2f(0, src.rows*0.3);
dstPoints[1] = Point2f(src.cols*0.25, src.rows*0.75);
dstPoints[2] = Point2f(src.cols*0.75, src.rows*0.25);
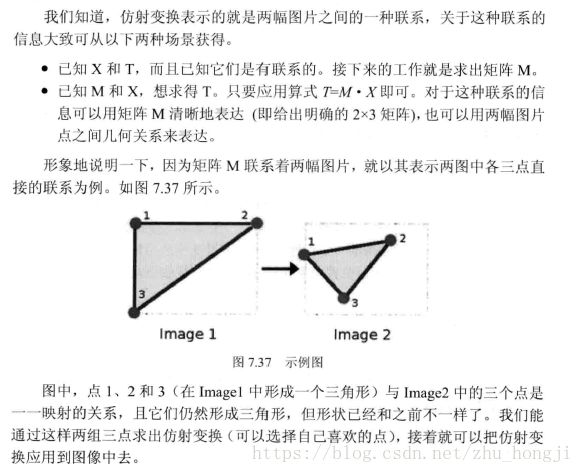
Mat M1 = getAffineTransform(srcPoints, dstPoints);//由三个点对计算变换矩阵
warpAffine(src, dst_warp, M1, src.size());//仿射变换
//第二种仿射变换的调用方式:直接指定角度和比例
//旋转加缩放
Point2f center(src.cols / 2, src.rows / 2);//旋转中心
double angle = 45;//逆时针旋转45度
double scale = 0.5;//缩放比例
Mat M2 = getRotationMatrix2D(center, angle, scale);//计算旋转加缩放的变换矩阵
warpAffine(src, dst_warpRotateScale, M2, Size(src.cols, src.rows), INTER_LINEAR);//仿射变换
//仿射变换—平移
Point2f srcPoints1[3];
Point2f dstPoints1[3];
srcPoints1[0] = Point2i(0, 0);
srcPoints1[1] = Point2i(0, src.rows);
srcPoints1[2] = Point2i(src.cols, 0);
dstPoints1[0] = Point2i(src.cols / 3, 0);
dstPoints1[1] = Point2i(src.cols / 3, src.rows);
dstPoints1[2] = Point2i(src.cols + src.cols / 3, 0);
Mat M3 = getAffineTransform(srcPoints1, dstPoints1);
warpAffine(src, dst_warpTransformation, M3, Size(src.cols + src.cols / 3, src.rows));
//仿射变换—翻转、镜像
Point2f srcPoints2[3];
Point2f dstPoints2[3];
srcPoints2[0] = Point2i(0, 0);
srcPoints2[1] = Point2i(0, src.rows);
srcPoints2[2] = Point2i(src.cols, 0);
dstPoints2[0] = Point2i(src.cols, 0);
dstPoints2[1] = Point2i(src.cols, src.rows);
dstPoints2[2] = Point2i(0, 0);
Mat M4 = getAffineTransform(srcPoints2, dstPoints2);
warpAffine(src, dst_warpFlip, M4, Size(src.cols, src.rows));
//flip(src, dst_warpFlip, 1);// flipCode:= 0 图像向下翻转
//> 0 图像向右翻转
//< 0 图像同时向下向右翻转
imshow("affine transformation1(三点法)", dst_warp);
imshow("affine transfoemation2(指定比例和角度)", dst_warpRotateScale);
imshow("affine transfoemation3(仿射变换平移)", dst_warpTransformation);
imshow("affine transformation4(仿射变换镜像)", dst_warpFlip);
waitKey(0);
return 0;
} 效果图:
(原图)
(仿射变换旋转的两种方法)
(仿射变换平移) (仿射变换翻转)
分析:仿射变换的五种变换平移,旋转,缩放,翻转(翻转镜像除了用三点法求仿射变换矩阵外还可以用flip函数实现)和错切,主要是一个仿射映射矩阵的设置,灵活的设置不同的变换矩阵则可以得到不同的变换效果,这里的仿射变换要想得到很好的效果如旋转以后图像的大小不变而且,图像还是位于窗口中心,就需要进行窗口大小调整还有旋转后,图像的平移。
3.2 透视变换
透视变换的API和仿射变换的API很像,原理也相同,不同的只是由之前的三点变为四点法求透视变换矩阵,变换矩阵也由2*3变为3*3;
(1)MatgetPerspectiveTransform(const Point2f* src, const Point2f* dst)
//参数const Point2f* src:原图的四个固定顶点
//参数const Point2f* dst:目标图像的四个固定顶点
//返回值:Mat型变换矩阵,可直接用于warpAffine()函数
//注意,顶点数组长度超4个,则会自动以前4个为变换顶点;数组可用Point2f[]或Point2f*表示
//注意:透视变换的点选取变为4个
(2)C++ void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())
//参数InputArray src:输入变换前图像
//参数OutputArray dst:输出变换后图像,需要初始化一个空矩阵用来保存结果,不用设定矩阵尺寸
//参数InputArray M:变换矩阵,用另一个函数getAffineTransform()计算
//参数Size dsize:设置输出图像大小
//参数int flags = INTER_LINEAR:设置插值方式,默认方式为线性插值(另一种WARP_FILL_OUTLIERS)
示例程序:
//透视变换
#include "stdafx.h"
#include
#include
#include
using namespace cv;
using namespace std;
int main(int argc, char* argv) {
Mat src, dst;
src = imread("C:/Users/59235/Desktop/image/girl5.jpg");
if (!src.data) {
printf("could not load image...\n");
return -1;
}
namedWindow("original image", CV_WINDOW_AUTOSIZE);
imshow("original image", src);
Mat dst_warp, dst_warpRotateScale, dst_warpTransformation, dst_warpFlip;
Point2f srcPoints[4];//原图中的四点 ,一个包含三维点(x,y)的数组,其中x、y是浮点型数
Point2f dstPoints[4];//目标图中的四点
srcPoints[0] = Point2f(0, 0);
srcPoints[1] = Point2f(0, src.rows);
srcPoints[2] = Point2f(src.cols, 0);
srcPoints[3] = Point2f(src.cols, src.rows);
//映射后的四个坐标值
dstPoints[0] = Point2f(src.cols*0.1, src.rows*0.1);
dstPoints[1] = Point2f(0, src.rows);
dstPoints[2] = Point2f(src.cols, 0);
dstPoints[3] = Point2f(src.cols*0.7, src.rows*0.8);
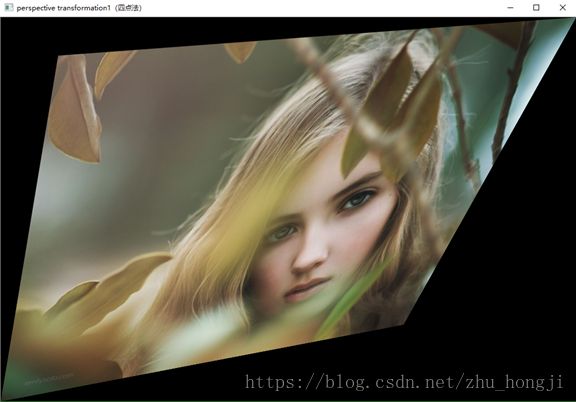
Mat M1 = getPerspectiveTransform(srcPoints, dstPoints);//由四个点对计算透视变换矩阵
warpPerspective(src, dst_warp, M1, src.size());//仿射变换
imshow("perspective transformation1(四点法)", dst_warp);
waitKey(0);
return 0;
} 效果图: (透视变换)