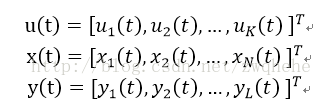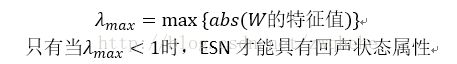回声状态网络(ESN)原理详解(附源码实现)

最近在看回声状态网络(Echo State Network)的内容，因为很少搜到关于Echo State  Network的快速入门讲解，所以打算写一下ESN的基本原理。

1、概念

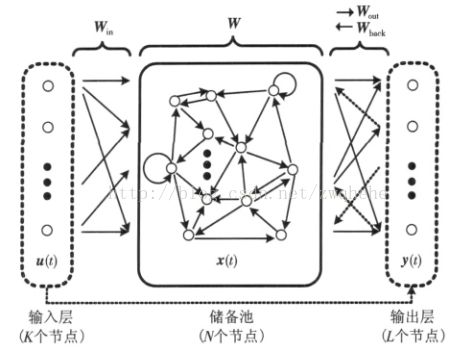
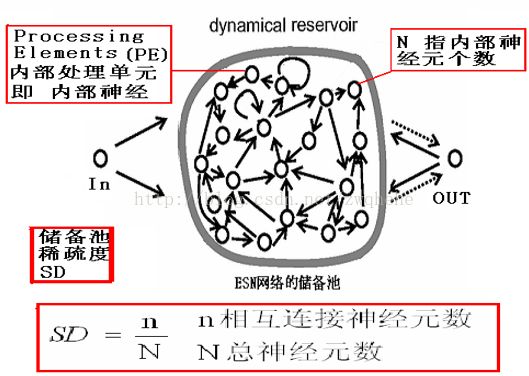
回声状态网络作为一种新型的递归神经网络(如上图)，也由输入层、隐藏层(即储备池)、输出层组成。其将隐藏层设计成一个具有很多神经元组成的稀疏网络，通过调整网络内部权值的特性达到记忆数据的功能，其内部的动态储备池(DR)包含了大量稀疏连接的神经元，蕴含系统的运行状态，并具有短期训记忆功能。ESN训练的过程，就是训练隐藏层到输出层的连接权值(Wout)的过程。总结如下三个特点：

（1）核心结构是一个随机生成且保持不变的储备池(Reservoir)

（2）其输出权值是唯一需要调整的部分

（3）简单的线性回归就可完成网络的训练

 

2、ESN的各个参数与公式。

2.1 节点与状态

图中t时刻的输入u(t)，一共有K个节点，储备池状态为x(t)，N个节点，输出为y(t)，L个节点。

        t 时刻的状态为：

  

2.2 连接矩阵与状态方程

图中的储备池就是常规神经网络的隐藏层，输入层到储备池的连接为Win(N*K阶)，储备池到下一个时刻储备池状态的连接为W(N*N阶)，储备池到输出层的连接为Wout(L*(K+N+L)阶)。另外还有一个前一时刻的输出层到下一时刻的储备池的连接Wback(N*L阶)，这个连接不是必须的(图中虚线表示)。

每一时刻输入u(t)，储备池都要更新状态，它的状态更新方程为：

式中，Win和Wback都是在最初建立网络的时候随机初始化的，并且固定不变。u(t+1)是这个时刻的输入，x(t+1)是这个时刻的储备池状态，x(t)是

上一个时刻的储备池状态，在t=0时刻可以用0初始化。f是DR内部神经元激活函数，通常使用双曲正切函数（tanh）。

注：在建模的时候，和一般的神经网络一样，会在连接矩阵上加上一个偏置量，所以输入u的是一个长度为1+K的向量，Win是一个[1+K, N]的矩阵，

x是一个长度为N的向量。

ESN的输出状态方程为：

式中，fout是输出层神经元激活函数。

到这里有了储备池状态，有了ESN输出方式，就可以根据目标输出y(target)来确定Wout，以使得y(t+1)和y(target)的差距尽可能小。这是一个简单

的线性回归问题，计算方法有多种，不再赘述。

2.3 储备池四个参数

储备池是该网络的核心结构，所谓的储备池就是随机生成的、大规模的、稀疏连接（SD通常保持1%-5%连接）的递归结构。

ESN的最终性能是由储备池的各个参数决定的，包括：储备池内部连接权谱半径SR、储备池规模N、储备池输入单元尺度IS、储备池稀疏程度SD。

（1）储备池内部连接权谱半径SR。其为连接权矩阵W的绝对值最大的特征值，记为λmax，λmax<1是保证网络稳定的必要条件；

（2）储备池规模N。其为储备池中神经元的个数，储备池的规模选择与样本个数有关，对网络性能影响很大，储备池规模越大，ESN对给定动态系统的描述越准确，但是会带来过拟合问题。

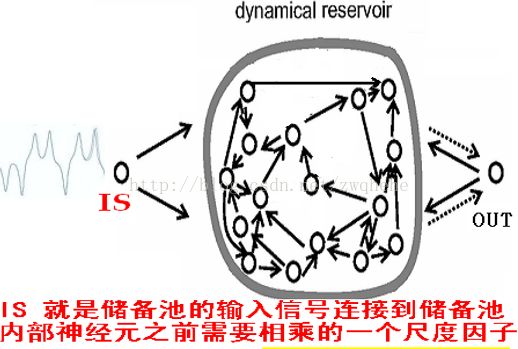
（3）储备池输入单元尺度IS。其为储备池的输入信号连接到储备池内部神经元之前需要相乘的一个尺度因子，即对输入信号进行一定的缩放。一般需要处理的对象非线性越强，IS越大。

（4）储备池稀疏程度SD。其表示储备池中神经元之间的连接情况，储备池中并不是所有神经元之间都存在连接。SD表示储备池中相互连接的神经元总数占总的神经元N的百分比，其值越大，非线性逼近能力越强。

 

3. ESN网络的训练

ESN的训练过程就是根据给定的训练样本确定系数输出连接权矩阵Wout的过程。其训练分为两个阶段：采样阶段和权值计算阶段

为了简单起见，这里假定Wback为0，同时输入到输出以及输出到输出连接权也假定为0。

3.1 采样阶段

采样阶段首先任意选定网络的初始状态，但是通常情况下选取网络的初始状态为0，即x(0)=0。

（1）训练样本（u(t), t=1,2,...,P）经过输入连接权矩阵Win被加入到储备池。

（2）按照前述两个状态方程，依次完成系统状态和输出y(t)的计算与收集。

为了计算输出连接权矩阵，需要从某一时刻m开始收集(采样)内部状态变量，并以向量为行构成矩阵B(P-m+1, N)，同时相应的样本数据y(t)也被收集，并构成一个列向量T(P-m+1, 1)。

3.2 权值计算阶段

权值计算就是根据在采样阶段收集到系统状态矩阵和样本数据，计算输出连接权Wout。因为状态变量x(t)和预测输出之间是线性关系，所以需要实现的目标就是利用预测输出，逼近期望输出y(t)：

至此，ESN网络训练已经完成，训练好的网络可以用于时间序列建模具体问题。

4. ESN实例

最后通过一个例子彻底理解最基本的ESN。数据集。python源码。（修改：链接已更新。如果以后在失效，可以在github上搜到类似代码和数据集，地址：https://github.com/alexander-rakhlin/ESN，现在我又在githhub搜了下ESN，能看到很多更好的代码，大家可以试试看）

在页面中下载python源码和数据集，在python2.7环境中运行。下面我改成了python3，并带有自己的注解。

数据就是一维的，代码中每次输入长度为1，预测数据中后一位的值，当然长度也是1:。

效果什么的，自己跑跑看。。。。

 

# -*- coding: utf-8 -*-
"""
A minimalistic Echo State Networks demo with Mackey-Glass (delay 17) data 
in "plain" scientific Python.
by Mantas Lukoševi�?ius 2012
http://minds.jacobs-university.de/mantas
"""
from numpy import *
from matplotlib.pyplot import *
import scipy.linalg

# 加载数据
#前2000个数据用来训练，2001-4000的数据用来测试。训练数据中，前100项用来初始化储备池，以让储备池中形成良好的回声之后再开始训练。
trainLen = 2000
testLen = 2000
initLen = 100

data = loadtxt('MackeyGlass_t17.txt')

# 绘制前1000条数据
figure(10).clear()
plot(data[0:1000])
title('A sample of data')

# 生成ESN储层
inSize = outSize = 1   # inSize 输入维数 K
resSize = 1000     # 储备池规模 N
a = 0.3 # 可以看作储备池更新的速度，可不加，即设为1.

random.seed(42)
#随机初始化 Win 和 W
Win = (random.rand(resSize, 1+inSize)-0.5) * 1   # 输入矩阵 N * (1+K)
W = random.rand(resSize, resSize)-0.5    # 储备池连接矩阵 N * N

# 对W进行防缩，以满足稀疏的要求。
# 方案 1 - 直接缩放 (快且有脏数据, 特定储层): W *= 0.135 
# 方案 2 - 归一化并设置谱半径 (正确, 慢):
print ('计算谱半径...')
rhoW = max(abs(linalg.eig(W)[0]))   # linalg.eig(W)[0]:特征值   linalg.eig(W)[1]:特征向量
W *= 1.25 / rhoW

# 为设计（收集状态）矩阵分配内存
X = zeros((1+inSize+resSize, trainLen-initLen))   # 储备池的状态矩阵x(t)：每一列是每个时刻的储备池状态。后面会转置
# 直接设置相应的目标矩阵
Yt = data[None, initLen+1:trainLen+1]    #输出矩阵:每一行是一个时刻的输出

# 输入所有的训练数据，然后得到每一时刻的输入值和储备池状态。
x = zeros((resSize, 1))
for t in range(trainLen):
    u = data[t]
    x = (1-a)*x + a*tanh( dot( Win, vstack((1, u)) ) + dot( W, x ) )   # vstack((1, u)):将偏置量1加入输入序列
    if t >= initLen:   # 空转100次后，开始记录储备池状态
        X[:, t-initLen] = vstack((1, u, x))[:, 0]
    
# 使用Wout根据输入值和储备池状态去拟合目标值，这是一个简单的线性回归问题，这里使用的是岭回归(Ridge Regression)。
reg = 1e-8  # 正则化系数
X_T = X.T
# Wout:  1 * 1+K+N
Wout = dot( dot(Yt, X_T), linalg.inv( dot(X, X_T) + \
    reg*eye(1+inSize+resSize) ) )   # linalg.inv矩阵求逆；numpy.eye()生成对角矩阵，规模:1+inSize+resSize，默认对角线全1，其余全0
#Wout = dot( Yt, linalg.pinv(X) )

# 使用训练数据进行前向处理得到结果
# run the trained ESN in a generative mode. no need to initialize here, 
# because x is initialized with training data and we continue from there.
Y = zeros((outSize, testLen))
u = data[trainLen]
for t in range(testLen):
    x = (1-a)*x + a*tanh( dot( Win, vstack((1, u)) ) + dot( W, x ) )
    y = dot( Wout, vstack((1, u, x)) )   # 输出矩阵(1 * 1+K+N)*此刻状态矩阵(1+K+N * 1)=此刻预测值
    Y[:,t] = y    # t时刻的预测值   Y: 1 * testLen
    # 生成模型
    u = y
    # 预测模型
    #u = data[trainLen+t+1] 

# 计算第一个errorLen时间步长的MSE
errorLen = 500
mse = sum( square( data[trainLen+1:trainLen+errorLen+1] - Y[0, 0: errorLen] ) ) / errorLen
print ('MSE = {0}'.format( str( mse ) ))
    
# 绘制测试集的真实数据和预测数据
figure(1).clear()
plot( data[trainLen+1:trainLen+testLen+1], 'g' )
plot( Y.T, 'b' )
title('Target and generated signals $y(n)$ starting at $n=0$')
legend(['Target signal', 'Free-running predicted signal'])

# 绘制储备池中前200个时刻状态(x(t))的前20个储层结点值
figure(2).clear()
plot( X[0:20,0:200].T )
title('Some reservoir activations $\mathbf{x}(n)$')

# 绘制输出矩阵
figure(3).clear()
bar( range(1+inSize+resSize), Wout.T )
title('Output weights $\mathbf{W}^{out}$')

show()