【码上实战】【立体匹配系列】经典PatchMatch: （3）随机初始化

下载源码，点击进入: Github - PatchMatchStereo
欢迎同学们在Github项目里讨论，如果觉得博主代码质量不错，给颗小星星，以及Follow Me！感激不尽！

算法效果图镇楼：

上一篇博客主类中，我们介绍了算法的主类：PatchMatchStereo，基本上大家对头文件已经了解了，从本篇开始，我们进入算法的具体实现部分。

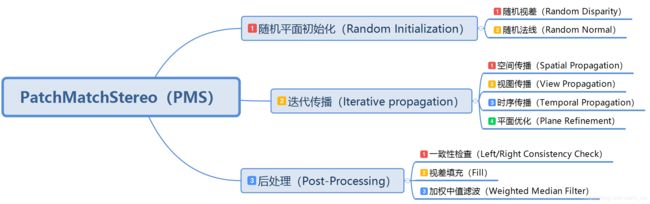
在第一篇编码教学博客框架中，我们有一张算法的架构图（下图），从图中我们可以清晰的看到算法的几个步骤，而第一个步骤，就是视差平面的随机初始化，本篇的内容也就是它！

视差平面的随机方法

我们知道，一个空间平面，你可以用参数来表达：$z=ax+by+c$，同时你也可以用平面上一个点$p(x,y,z)$以及平面法线$n(n_x,n_y,n_z)$来表示：$pl=(p,n)$。在PMS中，$z$就代表视差$d$，

如果选择第一种表达法，由于$a、b、c$是无边界的，可以随机到任何值，因此$d$就是无边界的，没有范围约束，这样显然不合适（要是随机个99999.9，那可怎么玩！）。

第二种表达法则可以限制$d$的范围，用户可以设定视差范围为$(d_{min},d_{max})$，对像素$(x,y)$，随机数生成器可在视差范围内随机视差值$d$组成平面上点$p(x,y,d)$。再随机一个单位法向量组成平面法线$n(n_x,n_y,n_z)$。这样平面可以表达成：$pl=(p,n)$，再换算成第一种方式，便于后面计算：$a=-\frac{n_x}{n_z}$，$b=-\frac{n_y}{n_z}$、$c=\frac{n_{x}x+n_{y}y+n_{z}d}{n_z}$。

代码解析

原理看懂了，我们再来看代码，先回顾下上篇关于视差平面的结构体定义：

/**
 * \brief 视差平面
 */
struct DisparityPlane {
	PVector3f p;
	DisparityPlane() = default;
	DisparityPlane(const float32& x,const float32& y,const float32& z) {
		p.x = x; p.y = y; p.z = z;
	}
	DisparityPlane(const sint32& x, const sint32& y, const PVector3f& n, const float32& d) {
		p.x = -n.x / n.z;
		p.y = -n.y / n.z;
		p.z = (n.x * x + n.y * y + n.z * d) / n.z;
	}

	/**
	 * \brief 获取该平面下像素(x,y)的视差
	 * \param x		像素x坐标
	 * \param y		像素y坐标
	 * \return 像素(x,y)的视差
	 */
	float32 to_disparity(const sint32& x,const sint32& y) const
	{
		return p.dot(PVector3f(float32(x), float32(y), 1.0f));
	}

	/** \brief 获取平面的法线 */
	PVector3f to_normal() const
	{
		PVector3f n(p.x, p.y, -1.0f);
		n.normalize();
		return n;
	}

	/**
	 * \brief 将视差平面转换到另一视图
	 * 假设左视图平面方程为 d = a_p*xl + b_p*yl + c_p
	 * 左右视图满足：(1) xr = xl - d_p; (2) yr = yl; (3) 视差符号相反(本代码左视差为正值，右视差为负值)
	 * 代入左视图视差平面方程就可得到右视图坐标系下的平面方程: d = -a_p*xr - b_p*yr - (c_p+a_p*d_p)
	 * 右至左同理
	 * \param x		像素x坐标
	 * \param y 	像素y坐标
	 * \return 转换后的平面
	 */
	DisparityPlane to_another_view(const sint32& x, const sint32& y) const
	{
		const float32 d = to_disparity(x, y);
		return { -p.x, -p.y, -p.z - p.x * d };
	}

	// operator ==
	bool operator==(const DisparityPlane& v) const {
		return p == v.p;
	}
	// operator !=
	bool operator!=(const DisparityPlane& v) const {
		return p != v.p;
	}
};

它的成员只有一个：

PVector3f p;

PVector3f是一个三维矢量结构体，在pms_types.h文件中同样有定义，这种最底层的结构体我们不细说，大家自己了解下，明白它有$x,y,z$三个分量就好。在视差平面结构体中,成员变量$p$就代表视差平面，它的三个分量$x,y,z$代表视差平面的三个参数$a,b,c$。

按照上面的说法，我们就是先随机一个视差$d$，再随机一个单位法向量$n$，通过它俩构造视差平面。咱们看代码：

void PatchMatchStereo::RandomInitialization() const
{
	const sint32 width = width_;
	const sint32 height = height_;
	if (width <= 0 || height <= 0 ||
		disp_left_ == nullptr || disp_right_ == nullptr ||
		plane_left_ == nullptr || plane_right_ == nullptr) {
		return;
	}
	const auto& option = option_;
	const sint32 min_disparity = option.min_disparity;
	const sint32 max_disparity = option.max_disparity;

	// 随机数生成器
	std::random_device rd;
	std::mt19937 gen(rd());
	const std::uniform_real_distribution<float32> rand_d(static_cast<float32>(min_disparity), static_cast<float32>(max_disparity));
	const std::uniform_real_distribution<float32> rand_n(-1.0f, 1.0f);

	for (int k = 0; k < 2; k++) {
		auto* disp_ptr = k == 0 ? disp_left_ : disp_right_;
		auto* plane_ptr = k == 0 ? plane_left_ : plane_right_;
		sint32 sign = (k == 0) ? 1:-1;
		for (sint32 y = 0; y < height; y++) {
			for (sint32 x = 0; x < width; x++) {
				const sint32 p = y * width + x;
				// 随机视差值
				float32 disp = sign * rand_d(gen);
				if (option.is_integer_disp) {
					disp = static_cast<float32>(round(disp));
				}
				disp_ptr[p] = disp;

				// 随机法向量
				PVector3f norm;
				if (!option.is_fource_fpw) {
					norm.x = rand_n(gen);
					norm.y = rand_n(gen);
					float32 z = rand_n(gen);
					while (z == 0.0f) {
						z = rand_n(gen);
					}
					norm.z = z;
					norm.normalize();
				}
				else {
					norm.x = 0.0f; norm.y = 0.0f; norm.z = 1.0f;
				}

				// 计算视差平面
				plane_ptr[p] = DisparityPlane(x, y, norm, disp);
			}
		}
	}
}

前面几句代码是一些变量、参数的获取，自不必说。

首先来看看这个来自于std标准库的随机数生成器uniform_real_distribution。顾名思义，它是一个均匀的实随机数生成器，它的构造参数是一个范围，这意味着它可以在给定的范围内进行均匀随机，这个太适合我们的随机过程了，我们对视差范围内的视差都没有偏好，都是等概率随机，随意均匀随机数生成器很适合，后面我将视差分布图示给大家看看，看是不是均匀分布的。

接下来，我们看看给这个随机数生成器的范围。给视差随机生成器的范围是设定的最小最大视差，这没什么疑问。给法线的是{-1.0,1.0}，这点其实也可以给其他值，最后我们会对随机的矢量进行单位化，所以范围长度不讲究，也可以是{-0.5,0.5}，但要中心对称，你不能给个{-2.0,1.0}之类的范围。

最后，我们来看逐像素的随机过程。因为我们要随机两张图，所以我用计数n来控制左右图像，k=0是随机左图，k=1随机右图。

随机的方法我上面也描述了，首先随机视差$d$：

// 随机视差值
float32 disp = sign * rand_d(gen);
if (option.is_integer_disp) {
	disp = static_cast<float32>(round(disp));
}
disp_ptr[p] = disp;

rand_d(gen)是随机器生成的视差值，disp是存储到图像视差数组里的值。这里有个sign，在左图的时候它是1，在右图的时候它是-1，这是因为代码中有一个设定：左图视差值和右图视差值互为相反数。这样的设定是为了让左影像当左视图进行传播及让右影像当左视图进行传播时，都满足$d=x_1-x_2$，使得即使图像对调都完全复用传播类，不用顾忌符号的问题。

option.is_integer_disp是PMS的一个参数，指定是否是整像素视差值，如果是整像素视差值，就把随机的小数转换为整数。

其次，随机法线$n$。

// 随机法向量
PVector3f norm;
if (!option.is_fource_fpw) {
	norm.x = rand_n(gen);
	norm.y = rand_n(gen);
	float32 z = rand_n(gen);
	while (z == 0.0f) {
		z = rand_n(gen);
	}
	norm.z = z;
	norm.normalize();
}
else {
	norm.x = 0.0f; norm.y = 0.0f; norm.z = 1.0f;
}

代码很简单，法线的每个分量都随机一个-1.0到1.0的小数值，最后对法线做一个单位化。这里需要注意的是法线的z分量不能为0，我们从上面的公式中也能看到，计算平面的参数的时候，n_z是分母，所以不能为0。代码的处理方式就是判断下是否为0，如果是就再次随机一个值，直到不为0（这很容易满足）。

option.is_fource_fpw是PMS的一个参数，指定是否是前端窗口模型（Fronto-parallel windows，这个模型我在PMS理论介绍第一篇介绍的很详细了，参见PMS：Slanted support windows倾斜支持窗模型）。在这个模型下，视差平面是固定的，且垂直于相机坐标系的Z轴，法线恒定为(0,0,1)。

最后，用视差和法线构造视差平面：

// 计算视差平面
plane_ptr[p] = DisparityPlane(x, y, norm, disp);

实验图

文字这么多，该来点图片解解乏了。我们在文件PatchMatchStereo.cpp中Match函数的实现体内，将迭代传播、一致性检查、视差填充步骤都注释掉，只保留了随机初始化，如下代码段：

bool PatchMatchStereo::Match(const uint8* img_left, const uint8* img_right, float32* disp_left)
{
	// 随机初始化
	RandomInitialization();
	// 计算灰度图
	//ComputeGray();
	// 计算梯度图
	//ComputeGradient();
	
	// 迭代传播
	//Propagation();
	
	// 平面转换成视差
	PlaneToDisparity();

	// 左右一致性检查
	if (option_.is_check_lr) {
		// 一致性检查
	//	LRCheck();
	}
	// 视差填充
	if (option_.is_fill_holes) {
	//	FillHolesInDispMap();
	}

	// 输出视差图
	if (disp_left && disp_left_) {
		memcpy(disp_left, disp_left_, height_ * width_ * sizeof(float32));
	}
	return true;
}

运行程序，左右视差图结果如下：

左影像

右影像

左视差图

右视差图

这就是随机初始化的结果，就是一团随机的麻点图，啥也看不出来，哈哈哈。可别说我代码有问题，原文也是如此：

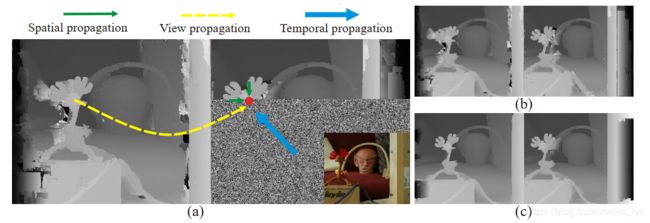
后经多次迭代传播，才能得到最后的好效果视差图，放心，后面我会展示的。

我们再把视差图导入PhotoShop看下值分布：

去除随机波动影响，分布还是非常均匀的，这就保证了视差(法线)范围内的等概率随机，公平公正。

好了，本篇就到这吧，下一篇带给大家的是PMS的代价计算器Cost Computer，敬请期待！

博主简介：
Ethan Li 李迎松
武汉大学 摄影测量与遥感专业博士

主方向立体匹配、三维重建

2019年获测绘科技进步一等奖（省部级）

爱三维，爱分享，爱开源
GitHub： https://github.com/ethan-li-coding
邮箱：[email protected]

个人微信：

欢迎交流！

喜欢博主的文章不妨关注一下博主的博客，感谢！
博客主页：https://blog.csdn.net/rs_lys