GAN生成对抗网络合集（四）：wGAN及wGAN-gp（附代码）

1 原始GAN存在问题

       实际训练中，GAN存在着训练困难、生成器和判别器的loss无法指示训练进程、生成样本缺乏多样性等问题。这与GAN的机制有关。
       GAN最终达到对抗的纳什均衡只是一个理想状态，而现实情况中得到的结果都是中间状态（伪平衡）。大部分的情况是，随着训练的次数越多判别器D的效果越好，会导致一直可以将生成器G的输出与真实样本区分开。
       这是因为生成器G是从低维空间向高维空间（复杂的样本空间）映射，其生成的样本分布空间Pg难以充满整个真实样本的分布空间Pr。即两个分布完全没有重叠的部分，或者它们重叠的部分可以忽略，这样就使得判别器D总会将它们分开。
       为什么可以忽略呢？放在二维空间中会更好理解一些。在二维平面中随机取两条曲线，两条曲线上的点可以代表二者的分布，要想判别器无法分辨它们，需要两个分布融合在一起，即它们之间需要存在重叠线段，然而这样的概率为0；另一方面，即使它们很可能会存在交叉点，但是相比于两条曲线而言，交叉点比曲线低一个维度，长度（测度）为0代表它只是一个点，代表不了分布情况，所以可以忽略。
       这样会带来什么后果呢？假设先将D训练得足够好，然后固定D，再来训练G，通过实验会发现G的loss无论怎么更新也无法收敛到最小值，而是无限接近log2。这个log2可以理解为Pg与Pr两个样本分布的距离。loss值恒定即表明G的梯度为0，无法再通过训练来优化自己。
       所以在原始GAN的训练中，判别器训练得太好，会使生成器梯度消失，生成器loss降不下去；判别器训练得不好，会使生成器梯度不准，四处乱跑。只有判别器训练到中间状态最佳，但是这个尺度很难把握，没有一个收敛判断的依据。甚至在同一轮训练的前后不同阶段，这个状态出现的时段都不一样，是个完全不可控的情况。

2 WGan原理

使用W-GAN网络进行图像生成时，网络将整个图像视为一种属性，其目的就是学习图像整个属性的数据分布，因而将生成图像分布Pg拟合为真实图像分布Pr是合理可行的。若期望的生成分布Pg不是当前的真实图像分布Pr，那么网络具体的收敛方向将会不可控，会出现训练失败的情况。

       WGan（Wasserstein Gan），Wasserstein是指Wasserstein距离，又叫Earth-Mover（EM）推土机距离。
       WGan的思想是将生成的模拟样本分布Pg与原始样本分布Pr组合起来，当成所有可能的联合分布的集合。然后可以从中采样得到真实样本与模拟样本，并能够计算二者的距离，还可以算出距离的期望值。这样就可以通过训练，让网络在所有可能的联合分布中对这个期望值取下界的方向优化，也就是将两个分布的集合拉到一起。这样原来的判别式就不再是判别真伪的功能了，而是计算两个分布集合距离的功能。所以将其称为评论器更加合适，同样，最后一层的sigmoid也需要去掉了。

核心意思就是：
原始GAN的D的loss都是真实样本和1作交叉熵，模拟样本和0作交叉熵；G的loss是模拟样本和1作交叉熵。
WGan的loss就是将真实样本和模拟样本形成联合分布，采样后给二者作差，D的目的是二者越大越好，G的目的是二者越小越好

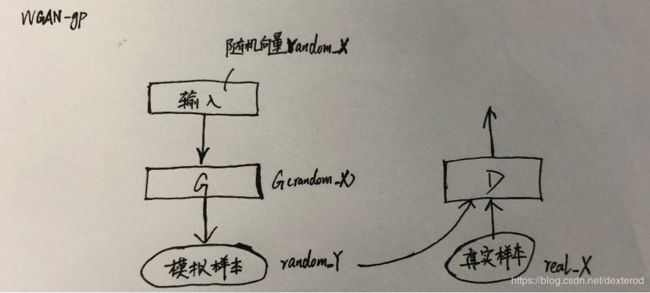
real_X   为真实数据
random_Y 为G生成的模拟数据
L = tf.reduce_mean(D(real_X)) - tf.reduce_mean(D(random_Y))
D_loss = tf.reduce_mean(D(random_Y)) - tf.reduce_mean(D(real_X)) 取反
G_loss = -tf.reduce_mean(D(random_Y))                            第一项与G无关

       但WGan也存在问题。对于前面说的梯度限制，WGAN直接使用Weight clipping方式太过生硬。每当更新完一次判别器的参数之后，就检查判别器的所有参数的绝对值有没有超过一个阈值，比如0.01，如果有的话就把这些参数截断（clipping）回[-0.01，0.01]的范围内。
       Lipschitz限制本意是当输入的样本稍微变化后，判别器给出的分数不能发生太剧烈的变化。通过在训练过程中保证判别器的所有参数有界，就保证了判别器不能对两个略微不同的样本给出天差地别的分数值，从而间接实现了Lipschitz限制。
       然而，这种渴望与判别器本身的目的相矛盾。在判别器中，是希望loss尽可能地大，才能拉大真假样本的区别，这种情况会导致在判别器中通过loss算出的梯度会沿着loss越来越大的方向变化，然而经过Weight clipping后每一个网络参数又被独立地限制了取值范围（如[-0.01，0.01]），这种结果只能是所有的参数走向极端，要么取最大值（如0.01）要么取最小值（如-0.01），判别器没能充分利用自身的模型能力，经过它回传给生成器的梯度也会跟着变差。
       如果判别器是一个多层网络，Weight clipping还会导致梯度消失或者梯度爆炸。原因是，如果我们把Clipping threshold设得稍微小了一点，每经过一层网络，梯度就变小一点，多层之后就会指数衰减；反之，如果设得稍微大了一点，每经过一层网络，梯度就会变大一点，多层之后就会指数爆炸。然而在实际应用中很难做到设置适宜，让生成器获得恰到好处的回传梯度。

3 WGan-gp原理

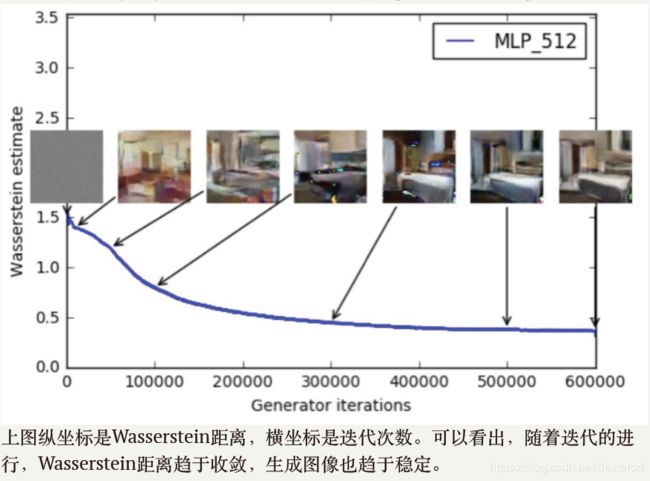
       在实际训练过程中，可以通过Wasserstein距离来度量模型收敛程度。

4 代码

# -*- coding: utf-8 -*-

##################################################################
#  1．引入头文件并加载mnist数据
##################################################################
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import os
import numpy as np
from scipy import misc,ndimage
import tensorflow.contrib.slim as slim
import time
from timer import Timer
# from tensorflow.python.ops import init_ops

mnist = input_data.read_data_sets("/Your/minist/dir/", one_hot=True)

batch_size = 100
width, height = 28, 28
mnist_dim = 784
random_dim = 10

tf.reset_default_graph()

##################################################################
#  2．定义生成器与判别器
##################################################################
def G(x):
    reuse = len([t for t in tf.global_variables() if t.name.startswith('generator')]) > 0
    with tf.variable_scope('generator', reuse=reuse):
        x = slim.fully_connected(x, 32, activation_fn=tf.nn.relu)
        x = slim.fully_connected(x, 128, activation_fn=tf.nn.relu)
        x = slim.fully_connected(x, mnist_dim, activation_fn=tf.nn.sigmoid)  # 生成器最终输出与原图相同纬度的数据作为模拟样本
    return x

def D(X):
    reuse = len([t for t in tf.global_variables() if t.name.startswith('discriminator')]) > 0
    with tf.variable_scope('discriminator', reuse=reuse):
        X = slim.fully_connected(X, 128, activation_fn=tf.nn.relu)
        X = slim.fully_connected(X, 32, activation_fn=tf.nn.relu)
        X = slim.fully_connected(X, 1, activation_fn=None)  # 输出维度为1的数值来表示结果
    return X

##################################################################
#  3．定义网络模型 和 loss
##################################################################
real_X = tf.placeholder(tf.float32, shape=[batch_size, mnist_dim])      # 真实样本数据
random_X = tf.placeholder(tf.float32, shape=[batch_size, random_dim])   # random_X为输入随机向量
random_Y = G(random_X)                                                  # random_Y为生成器G生成的模拟样本数据

eps = tf.random_uniform([batch_size, 1], minval=0., maxval=1.)
X_inter = eps * real_X + (1. - eps) * random_Y                          # 按照eps比例生成真假样本采样X_inter
grad = tf.gradients(D(X_inter), [X_inter])[0]
grad_norm = tf.sqrt(tf.reduce_sum((grad) ** 2, axis=1))
grad_pen = 10 * tf.reduce_mean(tf.nn.relu(grad_norm - 1.))              # 梯度惩罚项 (约束项)

D_loss = tf.reduce_mean(D(random_Y)) - tf.reduce_mean(D(real_X)) + grad_pen
G_loss = -tf.reduce_mean(D(random_Y))

##################################################################
#  4．定义优化器并开始训练
#     不直接显示图片，而是保存结果后查看；训练次数是100次，之所以这么多是因为不用伪平衡了，
#      D训练次数越多越好。
##################################################################
# 获得各个网络中各自的训练参数
t_vars = tf.trainable_variables()
d_vars = [var for var in t_vars if 'discriminator' in var.name]
g_vars = [var for var in t_vars if 'generator' in var.name]
print(len(t_vars), len(d_vars))  # 12 6

D_solver = tf.train.AdamOptimizer(1e-4, 0.5).minimize(D_loss, var_list=d_vars)
G_solver = tf.train.AdamOptimizer(1e-4, 0.5).minimize(G_loss, var_list=g_vars)

training_epochs = 100

config = tf.ConfigProto()
config.gpu_options.per_process_gpu_memory_fraction = 0.4

with tf.Session(config=config) as sess:
    sess.run(tf.global_variables_initializer())

    print(time.asctime(time.localtime(time.time())))

    if not os.path.exists('/Your/save/dir/wgan_result_pic/'):
        os.makedirs('/Your/save/dir/wgan_result_pic/')

    for epoch in range(training_epochs):
        timer = Timer()
        timer.tic()
        total_batch = int(mnist.train.num_examples/batch_size)  # 550

        # 遍历全部数据集
        for e in range(total_batch):
            for i in range(5):
                real_batch_X, _ = mnist.train.next_batch(batch_size)  # 取数据x:images
                random_batch_X = np.random.uniform(-1, 1, (batch_size, random_dim))
                _, D_loss_ = sess.run([D_solver, D_loss], feed_dict={real_X: real_batch_X, random_X: random_batch_X})

            random_batch_X = np.random.uniform(-1, 1, (batch_size, random_dim))
            _, G_loss_ = sess.run([G_solver, G_loss], feed_dict={random_X: random_batch_X})
        timer.toc()

        ##################################################################
        #  6．可视化
        ##################################################################
        if epoch % 10 == 0:
            # print(time.asctime(time.localtime(time.time())))
            print('epoch{}--> D_loss: {:.3f}, G_loss: {:.3}, speed: {:.3f}s'.format(epoch, D_loss_, G_loss_, timer.average_time*10))
            n_rows = 6
            check_imgs = sess.run(random_Y, feed_dict={random_X: random_batch_X}).reshape((batch_size, width, height))[:n_rows*n_rows]
            imgs = np.ones((width*n_rows+5*n_rows+5, height*n_rows+5*n_rows+5))  # (203, 203)
            # print(np.shape(imgs))#(203, 203)

            for i in range(n_rows*n_rows):
                num1 = (i % n_rows)
                num2 = np.int32(i/n_rows)
                imgs[5+5*num1+width*num1:5+5*num1+width+width*num1, 5+5*num2+height*num2:5+5*num2+height+height*num2] = check_imgs[i]

            misc.imsave('/Your/save/dir/wgan_result_pic/%s.png' % (epoch/10), imgs)

    print("完成!")

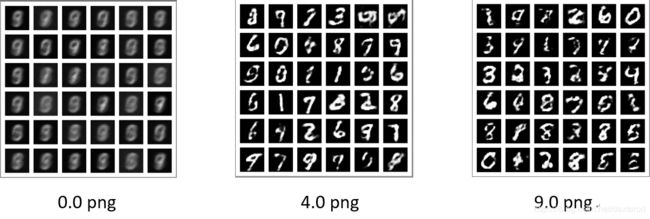
可视化结果：

       可以看到D_loss值逐渐减小，表明生成的模拟样本质量越来越高。Batch_size为100时，训练时间1次约10s。则Batch_size为10时，训练1次约100s。

5 与原始GAN的异同

• G和D的结构、输入和输出不一致；
• 模型的参数/输入/输出 因为WGan的定义loss值的方式不一样而改变；
• 优化器同样用Adam优化器，但优化参数发生了改变；
• 训练次数从3次改变为100次，D训练次数越多越准确。