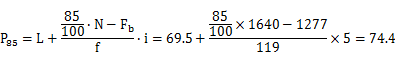分位数
本文内容
- 分位数
- 中位数
- 四分位数
- 百分位数
- 参考资料
- 演示
分位数
分位数(Quantile),也称分位点,是指将一个随机变量的概率分布范围分为几个等份的数值点,分析其数据变量的趋势。常用的有中位数、四分位数、百分位数等。
中位数
中位数(Medians)是一个统计学的专有名词,代表一个样本、种群或概率分布中的一个数值,可以将数值集合划分为相等的两部分,即,若设连续随机变量 X的分布函数为 F(X),那么满足条件 F(X)=1/2 ,称为 X 或分布 F 的中位数。中位数是用来衡量集中趋势的方法。对于一个有限的、有序的数集,位于中间位置的那个数值就是中位数,用 Me 表示。
中位数可以扩展到四分位数,即中位数再取中位数,变成四分位数。
四分位数
若设连续随机变量 X 的分布函数为 F(X),那么满足条件 F(X)=1/4 ,称为 X 或分布 F 的四分位数。四分位数通常用箱形图(Box Plots)表示。箱形图能显示出一组数据的最大值(Maximum)、最小值(Minimum)、中位数(Q2)、下四分位数(Q1)及上四分位数(Q3)。
四分位描述为,将 n 个数从小到大排列 xn=(x1,x2,x3,…,xn),那么 Q1,Q2,Q3 的位置 L:
当计算的位置为小数时,即 n 为奇数,其四分位数将在后面示例中介绍。
箱形图
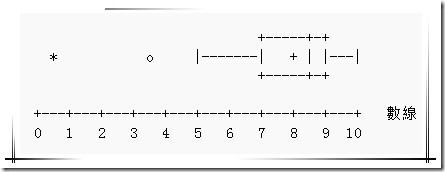
箱形图是于 1977年由美国著名统计学家约翰·图基(John Tukey)发明,如下所示:
图 1 箱形图
这组数据显示出:
- 最小值(Minimum)为 5
- 下四分位数(Q1)为 7
- 中位数(Q2,Median)为 8.5
- 上四分位数(Q3)为 9
- 最大值(Maximum)为 10
- 平均值为 8
- 四分位间距(Inter-quartile range,IQR)为 Q3-Q1=2,即 ΔQ,在区间 Q1-1.5ΔQ,Q3+1.5ΔQ 之外的值被视为应忽略(farout)。
- farout:在图上不予显示,仅标注一个符号。
- 最大值区间: Q3+1.5ΔQ
- 最小值区间: Q1-1.5ΔQ
- 最大值与最小值产生于这个区间。区间外的值被视为 outlier 显示在图上。
- mild outlier 为 3.5
- extreme outlier 为 0.5
图 2 正态分布 N(0,1σ2) 的箱形图和概率密度函数
不论 Q1,Q2,Q3 的变异量数数值为何,均视为一个分界点,以此将总数分成四个相等部分,可以通过 Q1 和 Q3 比较,分析其数据变量的趋势。
示例 1
某车间某月份的工人生产某产品的数量分别为 x=(13, 13.5, 13.8, 13.9, 14, 14.6, 14.8, 15, 15.2, 15.4, 15.7) 公斤,则三个四分位数的位置分别为:
即数组第3、第6、第9个工人的某种产品产量分别为下四分位数、中位数和上四分位数为:
Q1 = 13.8 公斤、Q2 = 14.6 公斤、Q3 = 15.2 公斤
示例 2
某车间某月份的工人生产某产品的数量分别为 x=(13, 13.5, 13.8, 13.9, 14, 14.6, 14.8, 15, 15.2, 15.4) 公斤,则三个四分位数的位置分别为:
即数组中的第 2.75 项、第 5.5 项、第 8.25 项分别为下四分位数、中位数和上四分位数。即:
Q1=0.25×第2项+0.75×第3项=0.25×13.5+0.75×13.8=13.73 (公斤)
Q2=0.5×第5项+0.5×第6项=0.5×14+0.5×14.6=14.3 (公斤)
Q3=0.75×第8项+0.25×第9项=0.75×15+0.25×15.2=15.05 (公斤)
若(n+1)为 4 的倍数,则确定四分数很简单;否则,若不是 4 的倍数,即小数,则四分位数是该小数的最大整数和最小整数位置上的值的平均数。
另外,权重的大小取决于两个整数位置距离的远近,距离越近,权数越大,距离越远,权数越小,权数之和等于 1。
示例 3
若有有序数组 x=(17, 19, 22, 24, 25, 28, 34),则四分位数:
Q1 的位置= (n + 1) / 4 = (7 + 1) / 4 = 2
Q3 的位置= 3*(n + 1) / 4 = 3*(7 + 1) / 4 = 6
则 Q1 与 Q3 分别为 19 和 28;IQR 四分位差为 Q3 − Q1=28-19=9
说明 50% 的数据集中在 19~28 之间,最大差异为 9。
百分位数
百分位数又称百分位分数(percentile),是一种相对地位量数,它是次数分布(Frequency Distribution,频数分布)中的一个点。把一个次数分布排序后,分为 100 个单位,百分位数就是次数分布中相对于某个特定百分点的原始分数,它表明在次数分布中特定个案百分比低于该分数。百分位数用P加下标 m(特定百分点)表示。譬如,若P30等于60,则其表明在该次数分布中有 30% 的个案低于 60 分。
百分位数运用在教育统计学中,如表现测验成绩时,又称 PR 值(Percentile ranks),用于描述一组数据某一百分位置的水平,多个百分位数结合应用,可全面描述一组观察值的分布特征;百分位数还可用于确定非正态分布资料的医学参考值范围。但应用百分位数时,样本含量要足够大,否则不宜取太靠近两端的百分位数。
计算公式为:
其中,
- Pm:第 m 百分位数;
- L:Pm所在组的组实下限;
- U:Pm所在组的组实上限;
- f:Pm所在组的次数;
- Fb:小于 L 的累积次数;
- Fa:大于 U 的累积次数。
示例 1
某省某年公务员考试考生分数分布如下表所示,预定取考分居前 15% 的考生进行面试,请划定面试分数线。
| 分数分组 |
次数 |
向上累积次数 |
向下累积次数 |
向上累积相对次数 |
| 95~99 |
7 |
1640 |
7 |
100% |
| 90~94 |
16 |
1633 |
23 |
99.57% |
| 85~89 |
53 |
1617 |
76 |
98.60% |
| 80~84 |
78 |
1564 |
154 |
95.37% |
| 75~79 |
90 |
1486 |
244 |
90.61% |
| 70~74 |
119 |
l396 |
363 |
85.12% |
| 65~69 |
159 |
1277 |
522 |
77.87% |
| 60~64 |
156 |
1118 |
678 |
68.17% |
| 55~59 |
140 |
962 |
818 |
58.66% |
| 50~54 |
145 |
822 |
963 |
50.12% |
| 45~49 |
140 |
677 |
1103 |
41.28% |
| 40~44 |
135 |
537 |
1238 |
32.74% |
| 35~39 |
130 |
402 |
1368 |
24.51% |
| 30~34 |
126 |
272 |
1494 |
16.59% |
| 25~29 |
78 |
146 |
1572 |
8.90% |
| 20~24 |
25 |
68 |
1597 |
4.15% |
| 15~19 |
20 |
43 |
1617 |
2.62% |
| 10~14 |
16 |
23 |
1633 |
1.40% |
| 5~9 |
7 |
7 |
1640 |
0.43% |
由于预定取考分居前 15% 的考生进行面试,即有85%的考生分数低于划定的分数线,由此可知,分数线在 70~74 这一组中。