统计学习方法(1) 梯度下降法和SMO算法实现SVM

SVM

SVM是深度学习之前的一种最常用的监督学习方法, 可以用来做分类也可以做回归. 它的本质和感知机类似, 但是额外增加了大间隔的优化目标. 结合前面提到的核技巧, 我们可以把SVM推广到非线性. 这样实现的分类器将有着非常好的性质, 让它一度成为"最优解".

LibSVM

在线性二分类SVM中,我们不止设置一个决策平面$w^{T}x+b=0$,还会有两个支持平面$w^{T}x+b=-1$和$w^{T}x+b=1$. 如果我们假设数据是线性可分的, 那么决策平面一定位于两类样本之间. 而现在我们想从两类样本之间确定一个最好的超平面,这个超平面满足的性质是到两类样本的最小距离最大.很自然的, 我们可以看出这个超平面到两类样本的最小距离应该相等. 这时上面的支持超平面就派上用场了. 设到超平面最近的两个样本是$x_{+}$和$x_{-}$, 样本距离$d=\frac{w^{T}x+b}{||w||}$, 也就是$w^T{x}_{+}+b=-(w^T{x}_{-}+b)=C$. 又因为w的缩放对超平面的性质没有影响, 我们不妨让C = 1, 即两个样本$x_{+}$和$x_{-}$会分别落在$w^{T}x+b=1$和$w^{T}x+b=-1$超平面上. 其他样本都在这两个超平面以外.
如果用上面的一系列假设, 我们的损失函数就应该是: 如果正样本越过了$w^{T}x+b=1$超平面, 即$w^{T}x+b<1$那么它受到随距离线性增长的惩罚. 同样如果正样本越过了$w^{T}x+b=-1$超平面, 即$w^{T}x+b>-1$也受到惩罚. 如果我们设y是样本标签,正样本为+1,负样本为-1. 则我们有保证两类样本到决策超平面的最小距离相等的新型感知机
$$L(w,b)=\frac{ReLU(-y_i(w^T{x}_i+b)+1)}{||w||}$$
同样的道理, 等价于
$$L(w,b)=ReLU(-y_i(w^T{x}_i+b)+1)$$
到此还不算结束, 因为我们还想要这个最小距离最大化. 我们知道$d=\frac{w^{T}x+b}{||w||}$, 而$|w^T x_++b| = |w^T x_-+b| = 1 $,即$d=\frac{1}{||w||}$, 也就是最大化距离, 只需要最小化w即可. 最小化一个参数常用的做法是正则化, 也就是对w施加L2的惩罚(L1的惩罚性质较差, 容易让w为0).这样我们就得到了最大化最小距离的损失.
$$minimize\frac{1}{2}||w|{|}_2^2$$
我们把上面两个损失函数加起来, 并给感知机正确分类的一项乘上一个常数系数, 用来调控(正确分类) vs (最大化间隔)两个目标的重要程度.
$$minimizeL(w,b)=\frac{1}{2}||w|{|}_2^2+C\ast ReLU(-y_i(w^T{x}_i+b)+1)$$
优化这个无约束的优化问题就能得到线性的二分类SVM, 我们用Pytorch的自动求导来实现梯度下降, 优化这个目标函数看看效果.

import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn.functional as F
import torch.nn as nn
import matplotlib
import random

torch.manual_seed(2020)
n = 50

Xp = torch.randn(n,2)
Xp[:,0] = (Xp[:,0]+3)
Xp[:,1] = (Xp[:,1]+4)
A = torch.tensor([[-1.,0.8],[2,1]])
Xp = Xp.mm(A)

Xn = torch.randn(n,2)
Xn[:,0] = (Xn[:,0]-1)
Xn[:,1] = (Xn[:,1]-2)
A = torch.tensor([[-0.5,1],[1,0.5]])
Xn = Xn.mm(A)

X = torch.cat((Xp,Xn),axis = 0)
y = torch.cat((torch.ones(n),-1*torch.ones(n)))
y = y.reshape(-1,1)


class LibSVM:
    def __init__(self, C = 1, lr = 0.01):
        '''
        超参数包括松弛变量C和学习率lr
        要学习的参数是一个线性超平面的权重和偏置
        '''
        self.C = C
        self.lr = lr
        self.weights = None
        self.bias = None
    
    def train(self):
        self.weights.requires_grad = True
        self.bias.requires_grad = True
        
    def eval(self):
        self.weights.requires_grad = False
        self.bias.requires_grad = False
    
    def fit(self, X, y, max_iters = 1000):
        '''
        X是数据张量, size(n,m)
        数据维度m, 数据数目n
        y是二分类标签, 只能是1或-1
        '''
        n,m = X.shape
        y = y.reshape(-1,1)
        self.weights = torch.randn(m,1)
        self.bias = torch.randn(1)
        self.train()
        
        for step in range(max_iters):
            out = X.mm(self.weights)+self.bias # 前向计算
            # 损失计算
            loss = 0.5*self.weights.T.mm(self.weights)+\
            self.C*torch.sum(F.relu(-y*out+1))
            # 自动求导
            loss.backward()
            # 梯度下降
            self.weights.data -= self.lr*self.weights.grad.data
            self.bias.data -= self.lr*self.bias.grad.data
            self.weights.grad.data.zero_()
            self.bias.grad.data.zero_()
            
        return loss
    
    def predict(self, x, raw = False):
        self.eval()
        out = x.mm(self.weights)+self.bias
        if raw: return out
        else: return torch.sign(out)
        
    def show_boundary(self, low1, upp1, low2, upp2):
        # meshgrid制造平面上的点
        x_axis = np.linspace(low1,upp1,100)
        y_axis = np.linspace(low2,upp2,100)
        xx, yy = np.meshgrid(x_axis, y_axis)
        data = np.concatenate([xx.reshape(-1,1),yy.reshape(-1,1)],axis = 1)
        data = torch.tensor(data).float()
        # 用模型预测
        out = self.predict(data, raw = True).reshape(100,100)
        out = out.numpy()
        Z = np.zeros((100,100))
        Z[np.where(out>1)] = 1.
        Z[np.where(out<-1)] = -1.
        # 绘制支持边界
        plt.figure(figsize=(8,6))
        colors = ['aquamarine','seashell','palegoldenrod']
        plt.contourf(xx, yy, Z, cmap=matplotlib.colors.ListedColormap(colors))
        # 绘制决策边界
        slope = (-self.weights[0]/self.weights[1]).data.numpy()
        b = (-self.bias/self.weights[1]).data.numpy()
        xx = np.linspace(low1, upp1)
        yy = slope*xx+b
        plt.plot(xx,yy, c = 'black')

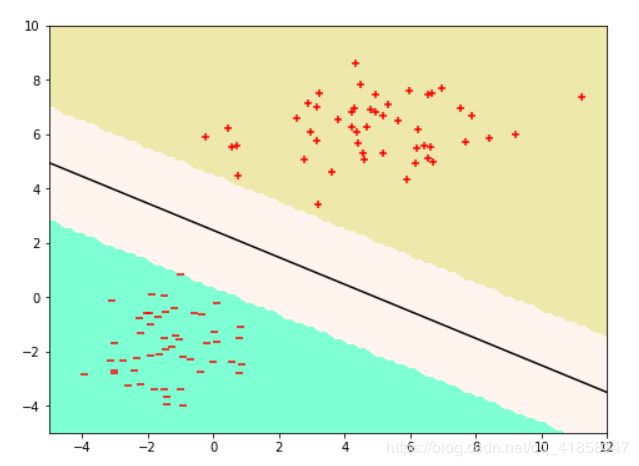
model = LibSVM()
model.fit(X,y)
model.show_boundary(-5,12,-5,10)
plt.scatter(X[:n,0].numpy(),X[:n,1].numpy() , marker = '+', c = 'r')
plt.scatter(X[n:,0].numpy(),X[n:,1].numpy() , marker = '_', c = 'r')

Kernel SVM

有时, 我们需要的是超越超平面的决策边界, 它应该能容忍非线性可分的两类样本, 并给出非线性的解. 这一点仅靠上面的方法是无法实现的, 为此我们可以把核技巧带到LibSVM中, 得到二分类的KerbSVM. 复习一下核方法, 我们使用核方法的核心思想是在向量内积得到的标量上进行非线性变换, 从而间接实现高维映射.
那么怎么把内积带到上面的线性模型里呢? 观察到权重w和数据点x的维度相同, 那么如果我们把w写成x的线性组合, 就能得到x和x的内积. 即
$$w=\sum _{i=1}^N{\alpha }_i{x}_i^T$$
$$y=\sum _{i=1}^N{\alpha }_{i}x{x}_i^T$$
在内积上套用核函数就有非线性的广义线性模型, 常用的非线性核函数有高斯核, 多项式核等等
$$k(x,y)=(x{y}^T{)}^d$$
$$k(x,y)=exp(-\sigma ||x-y|{|}^2)$$
$$y=\sum _{i=1}^N{\alpha }_i\varphi (x)\varphi (x_i{)}^T+b=\sum _{i=1}^N{\alpha }_{i}k(x,x_i)+b$$
把这个新的计算式代入之前的损失函数, 得到新的, 核函数版本的bSVM的损失函数
$$minimizeL(w,b)=\frac{1}{2}||w|{|}_2^2+C\ast ReLU(-y_i(\sum _{i=1}^N{\alpha }_{i}k(x,x_i)+b)+1)=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_{j}k(x_i,x_j)+C\ast ReLU(-y_i(\sum _{i=1}^N{\alpha }_{i}k(x,x_i)+b)+1)$$
优化它, 得到的就是n维向量alpha和一个偏置b. 那么你可能会说, 如果是这样, 我们的数据集越大, 要计算的alpha不也会越大吗? 而且要执行运算的话, 是不是就需要保存训练时使用的全部$x_i$, 对每个$x_i$都和当前x做核函数运算再做线性组合, 才能得到结果呢? 事实也是如此, 因此, 在大规模数据上执行核SVM算法时, 我们并不会用所有的$x_i$来做线性组合产生w, 我们可以只取一部分的$x_i$来减少运算量.

class KerbSVM:
    def __init__(self, C = 1, sigma = None, lr = 0.01):
        self.C = C
        self.lr = lr
        self.sigma = sigma
        self.weights = None
        self.bias = None
        
    
    def train(self):
        self.weights.requires_grad = True
        self.bias.requires_grad = True
        
    def eval(self):
        self.weights.requires_grad = False
        self.bias.requires_grad = False
    
    def ker_func(self, x1, x2, sigma = None):
        '''
        高斯核函数, sigma是高斯核的带宽
        x1, x2是矩阵, 函数计算x1和x2的核矩阵
        '''
        n1,n2 = x1.shape[0],x2.shape[0]
        if sigma is None:
            sigma = 0.5/x1.shape[1]
        K = torch.zeros((n1,n2))
        for i in range(n2):
            square = torch.sum((x1-x2[i])**2, axis = 1)
            K[:,i] = torch.exp(-square)
        return K
        
    
    def fit(self, X, y, max_iters = 1000, print_info = False):
        '''
        X是数据张量, size(n,m)
        数据维度m, 数据数目n
        y是二分类标签, 只能是1或-1
        '''
        n,m = X.shape
        y = y.reshape(-1,1)
        self.weights = torch.zeros((n,1))
        self.bias = torch.zeros(1)
        self.train()
        
        # 计算数据集X的核矩阵
        K_mat = self.ker_func(X,X,self.sigma)
        
        for step in range(max_iters):
            out = K_mat.mm(self.weights)+self.bias # 前向计算
            # 损失计算
            rloss = 0.5*self.weights.T.mm(K_mat).mm(self.weights)
            closs = self.C*torch.sum(F.relu(-y*out+1))
            # 自动求导
            loss = rloss+closs
            loss.backward()
            # 梯度下降
            self.weights.data -= self.lr*self.weights.grad.data
            self.bias.data -= self.lr*self.bias.grad.data
            self.weights.grad.data.zero_()
            self.bias.grad.data.zero_()
            if (step+1)%20==0 and print_info:
                print("step %d, regularization loss: %.4f, classification loss: %.4f"%(step+1,rloss,closs))
        
        self.X = X
        return loss
    
    def predict(self, x, raw = False):
        self.eval()
        out = self.ker_func(x,self.X).mm(self.weights)+self.bias
        if raw: return out
        else: return torch.sign(out)
        
    def show_boundary(self, low1, upp1, low2, upp2):
        # meshgrid制造平面上的点
        x_axis = np.linspace(low1,upp1,100)
        y_axis = np.linspace(low2,upp2,100)
        xx, yy = np.meshgrid(x_axis, y_axis)
        data = np.concatenate([xx.reshape(-1,1),yy.reshape(-1,1)],axis = 1)
        data = torch.tensor(data).float()
        # 用模型预测
        out = self.predict(data, raw = True).reshape(100,100)
        out = out.numpy()
        Z = np.zeros((100,100))
        Z[np.where(out>0)] = 1.
        Z[np.where(out>1)] += 1.
        Z[np.where(out<-1)] = -1.
        # 绘制支持边界
        plt.figure(figsize=(8,6))
        colors = ['aquamarine','seashell','paleturquoise','palegoldenrod']
        plt.contourf(xx, yy, Z, cmap=matplotlib.colors.ListedColormap(colors))

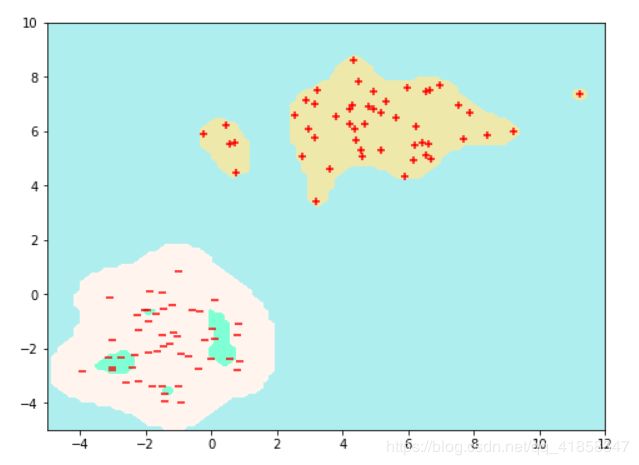
model = KerbSVM(C=1, lr = 0.01)
model.fit(X,y,max_iters = 2000)
model.show_boundary(-5,12,-5,10)
plt.scatter(X[:n,0].numpy(),X[:n,1].numpy() , marker = '+', c = 'r')
plt.scatter(X[n:,0].numpy(),X[n:,1].numpy() , marker = '_', c = 'r')

对偶SVM

上面的梯度下降优化方法是可行的, 但是考虑到SVM对超参数很敏感, 我们需要不断地尝试调整参数才能找到一组比较好的参数(比如上面的松弛变量C和高斯核带宽sigma). 这就要求我们可能需要进行多次的交叉验证. 但是多次交叉验证的训练开销相对大, 这就成为了SVM的应用上最大的阻碍.
但是我们对SVM的几十年的研究并不是白费的, 研究者们总结出了一套把SVM转为对偶问题的方法, 并在约束的对偶问题里进行基于二次规划的坐标下降优化. 我们还会用一些启发式的方法帮助我们快速找到解.
我们先推导一下对偶形式的SVM, 我们改写SVM的优化目标, 把ReLU的hinge loss那一项写成一般的不等式约束形式, 同时优化目标函数是w的L2-norm.
$$minimize\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i$$
$$s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i$$
$${\xi }_i\ge 0$$
其中xi是和hinge loss的意义相似的, 把不等式约束软化的方法. 我们用xi放松对边界的限制, 但是随着xi增加, 我们会受到额外的L1惩罚. 解它的对偶问题有
Lagrangian:
$$L(w,b,\xi ,\alpha ,r)=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i+\sum _{i=1}^N{\alpha }_i[1-{\xi }_i-y_i(w^T{x}_i+b)]-\sum _{i=1}^N{r}_i{\xi }_i$$
pd2zeros:
$$\frac{\partial L}{\partial w}=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0$$
$$\frac{\partial L}{\partial b}=-\sum _{i=1}^N{\alpha }_i{y}_i=0$$
$$\frac{\partial L}{\partial {\xi }_i}=C-{\alpha }_i-r_i=0$$
回代原优化问题
$$minimize\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
这是另一种推导SVM的线路, 因为是有约束的凸优化形式, 我们可以很自然的把问题推广为对偶问题
$$maximiz{e}_{\alpha ,r}mi{n}_{w,b,\xi }L(w,b,\xi ,\alpha ,r)$$
$${\alpha }_i\ge 0,r_i\ge 0$$
$$\sum _{i=1}^N{\alpha }_i{y}_i=0$$
$$C-{\alpha }_i-r_i=0$$
凸优化的对偶问题最优解和原问题相同, 我们可以直接处理对偶问题
$$maximiz{e}_{\alpha }\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
$$0\ge {\alpha }_i\le C$$
$$\sum _{i=1}^N{\alpha }_i{y}_i=0$$
因为有向量内积, 我们还能很自然引入核函数实现非线性
$$maximiz{e}_{\alpha }\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}k(x_i,x_j)$$
到这里, 我们推翻了前面的无约束版本的SVM, 引入了这种对偶版本的SVM. 对一般的问题, 我们也不知道一个凸优化的原问题和对偶问题哪一个比较容易求解, 但是SVM的对偶问题是极为特殊的形式, 我们要优化的是对偶问题里的alpha, 一旦求到了alpha的最优解, 我们就拿到了最终的SVM计算式
$$y=\sum _{i=1}^N{\alpha }_i{y}_{i}k(x,x_i)+b$$
b可以选择非0alpha对应的数据点计算=1或者=-1的恒等式得到. 那么任务就是如何求解对偶问题, 这个对偶问题由一个等式约束, 一个不等式约束和一个优化目标组成. 现在, 我们就讲一下怎么用高效的方法解这个约束优化.

SMO算法

SMO使用坐标下降的方法求解该问题, 每个优化step, 我们选择所有alpha中的两个alpha, 改变它们而固定其他. 又因为存在等式约束${\sum }_{i=1}^N{\alpha }_i{y}_i=0$, 把它代入优化目标后要处理的变量只有一个,而且是一个关于该变量的二次函数. 剩下的二次函数和不等式约束组成了一个二次规划问题.
$$maximiz{e}_{{\alpha }_i,{\alpha }_j}Q({\alpha }_i,{\alpha }_j)$$
$$0\ge {\alpha }_i\le C$$
$$0\ge {\alpha }_j\le C$$
$$\sum _{i=1}^N{\alpha }_i{y}_i=0$$
我们每次优化都计算这个二次规划的最优解, 把它更新到新的迭代点, 而且我们保证这样的更新比梯度上升更有效, 因为它每次更新都保证让损失函数上升.
好, 那么现在的问题就是求这个二次规划的闭式解, 只要有了闭式解, 可以想象, 我们就能通过多次调用闭式解就完成优化, 而不需要执行反向传播和梯度下降的多次迭代.
首先我们计算无约束时的最优解, 这个过程其实就是初中的二次函数极值问题
$$Q({\alpha }_1,{\alpha }_2)={\alpha }_1+{\alpha }_2-\frac{1}{2}{K}_{1,1}{y}_1^2{\alpha }_1^2-\frac{1}{2}{K}_{2,2}{y}_2^2{\alpha }_2^2-K_{1,2}{y}_1{y}_2{\alpha }_1{\alpha }_2-y_1{\alpha }_1\sum _i^{rest}{\alpha }_i{y}_i{K}_{i,1}-y_2{\alpha }_2\sum _i^{rest}{\alpha }_i{y}_i{K}_{i,2}+C$$
我们由等式约束可以写出
$${\alpha }_1{y}_1+{\alpha }_2{y}_2=\zeta =-\sum _i^{rest}{\alpha }_i{y}_i$$
$${\alpha }_1=\zeta y_1-{\alpha }_2{y}_1{y}_2$$
回代到二次函数Q中, 得到一元二次函数
$$Q({\alpha }_1,{\alpha }_2)=-\frac{1}{2}{K}_{1,1}(\zeta -y_1^2{\alpha }_1^2{)}^2-\frac{1}{2}{K}_{2,2}{\alpha }_2^2-K_{1,2}(\zeta -{\alpha }_2{y}_2)y_2{\alpha }_2-(\zeta -{\alpha }_2{y}_2)\sum _i^{rest}{\alpha }_i{y}_i{K}_{i,1}-y_2{\alpha }_2\sum _i^{rest}{\alpha }_i{y}_i{K}_{i,2}+{\alpha }_1+{\alpha }_2+C$$
$$\frac{\partial Q}{\partial {\alpha }_2}=-(K_{1,1}+K_{2,2}-2K_{1,2}){\alpha }_2+K_{1,1}\zeta y_2-K_{1,2}\zeta y_2+y_2\sum _i^{rest}{\alpha }_i{y}_i{K}_{i,1}-y_2\sum _i^{rest}{\alpha }_i{y}_i{K}_{i,2}-y_1{y}_2+y_2^2=0$$
剩下的就是纯粹的计算, 算到最后我们发现, 新的${\alpha }_2$可以用旧的${\alpha }_2$表示.
$${\alpha }_2^{new}={\alpha }_2^{old}+\frac{y_2(E_1-E_2)}{\eta }$$
其中E是预测值与真实值的误差$E_i=f(x_i)-y_i$, $\eta =K_{1,1}+K_{2,2}-K_{1,2}$
下一步就是考虑约束, 给出约束下的极值点. 我们考虑的约束是所谓"方形约束".


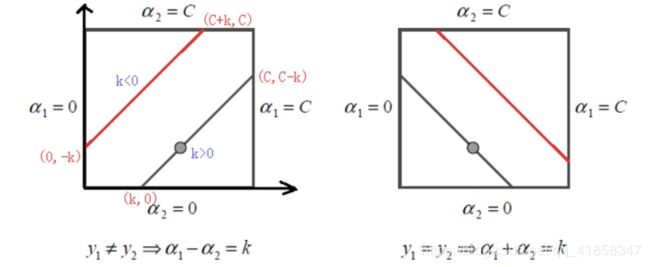
我们额外计算一下上下界, 并作clip就能计算出${\alpha }_2$的值了, 然后我们用恒等式把${\alpha }_1$的值也算出来, 这样就结束了一次更新. SMO的步骤大致如此

选择要更新的参数

每次更新我们都会面对所有n个$\alpha$, 那么要更新的是哪个呢. 我们从误差出发, 我们上面定义的E是预测偏移标签的值, 我们永远选择误差最大的那一个$\alpha$作为${\alpha }_2$更新, ${\alpha }_1$的话随机选取即可.

class SVC:
    def __init__(self, C = 1, sigma = None):
        self.C = C
        self.sigma = sigma
        self.weights = None
        self.bias = None
    
    def ker_func(self, x1, x2, sigma = None):
        '''
        高斯核函数, sigma是高斯核的带宽
        x1, x2是矩阵, 函数计算x1和x2的核矩阵
        '''
        n1,n2 = x1.shape[0],x2.shape[0]
        if sigma is None:
            sigma = 0.5/x1.shape[1]
        K = np.zeros((n1,n2))
        for i in range(n2):
            square = np.sum((x1-x2[i])**2, axis = 1)
            K[:,i] = np.exp(-square)
        return K
        
    def predict(self, x, raw = False):
        out = self.ker_func(x,self.X).dot(self.weights*self.y)+self.bias
        if raw: return out
        else: return np.sign(out)
    
    def fit(self, X, y, max_iters = 100):
        '''
        X是数据张量, size(n,m)
        数据维度m, 数据数目n
        y是二分类标签, 只能是1或-1
        '''
        n,m = X.shape
        self.X = X
        y = y.reshape(-1,1)
        self.y = y
        self.weights = np.zeros((n,1))
        self.bias = np.zeros(1)
        
        # 计算数据集X的核矩阵
        K_mat = self.ker_func(X,X,self.sigma)
        alpha = self.weights
        b = self.bias
        C = self.C
        
        for t in range(max_iters):
            #首先为各变量计算err
            con1 = alpha > 0
            con2 = alpha < C

            y_pred = K_mat.dot(alpha)+b
            err1 = y * y_pred - 1
            err2 = err1.copy()
            err3 = err1.copy()
            err1[(con1 & (err1 <= 0)) | (~con1 & (err1 > 0))] = 0
            err2[((~con1 | ~con2) & (err2 != 0)) | ((con1 & con2) & (err2 == 0))] = 0
            err3[(con2 & (err3 >= 0)) | (~con2 & (err3 < 0))] = 0
            # 算出平方和并取出使得“损失”最大的 idx
            err = err1 ** 2 + err2 ** 2 + err3 ** 2
            i = np.argmax(err)
            j = i
            while j==i:
                j = random.randint(0,n-1)

            #为i和j计算函数值E = f(x)-y
            e1 = self.predict(X[i:i+1],raw = True)-y[i]
            e2 = self.predict(X[j:j+1],raw = True)-y[j]
            #计算内积差
            dK = K_mat[i][i]+K_mat[j][j]-2*K_mat[i][j]
            #计算上下界
            if y[i]!=y[j]:
                L = max(0,alpha[i]-alpha[j])
                H = min(C,C+alpha[i]-alpha[j])
            else:
                L = max(0,alpha[i]+alpha[j]-C)
                H = min(C,alpha[i]+alpha[j])
            #更新参数的最优值
            alpha1_new = alpha[i]-y[i]*(e1-e2)/dK
            #考虑上下界后的更新值
            alpha1_new = np.clip(alpha1_new, L, H)
            alpha[j:j+1] += y[i]*y[j]*(alpha[i]-alpha1_new)
            alpha[i:i+1] = alpha1_new

            #找支持向量并修正b
            b -= b
            indices = [i for i in range(n) if 0<alpha[i]<C]
            for i in indices:
                b+=(1/y[i]-np.sum(alpha*K_mat[i]*y))
            if len(indices):
                b /= len(indices)
        
        # 保留支持向量和对应的权值
        '''
        indices = np.where(alpha[:,0]>0)
        self.X = self.X[indices]
        self.y = self.y[indices]
        self.weights = self.weights[indices]
        '''
        
        return alpha, b
        
    def show_boundary(self, low1, upp1, low2, upp2):
        # meshgrid制造平面上的点
        x_axis = np.linspace(low1,upp1,100)
        y_axis = np.linspace(low2,upp2,100)
        xx, yy = np.meshgrid(x_axis, y_axis)
        data = np.concatenate([xx.reshape(-1,1),yy.reshape(-1,1)],axis = 1)
        # 用模型预测
        out = self.predict(data, raw = True).reshape(100,100)
        Z = np.zeros((100,100))
        Z[np.where(out>0)] = 1.
        Z[np.where(out>1)] += 1.
        Z[np.where(out<-1)] = -1.
        # 绘制支持边界
        plt.figure(figsize=(8,6))
        colors = ['aquamarine','seashell','paleturquoise','palegoldenrod']
        plt.contourf(xx, yy, Z, cmap=matplotlib.colors.ListedColormap(colors))


model = SVC()
model.fit(X.numpy(),y.numpy(),max_iters = 500)
model.show_boundary(-5,12,-5,10)
plt.scatter(X[:n,0].numpy(),X[:n,1].numpy() , marker = '+', c = 'r')
plt.scatter(X[n:,0].numpy(),X[n:,1].numpy() , marker = '_', c = 'r')

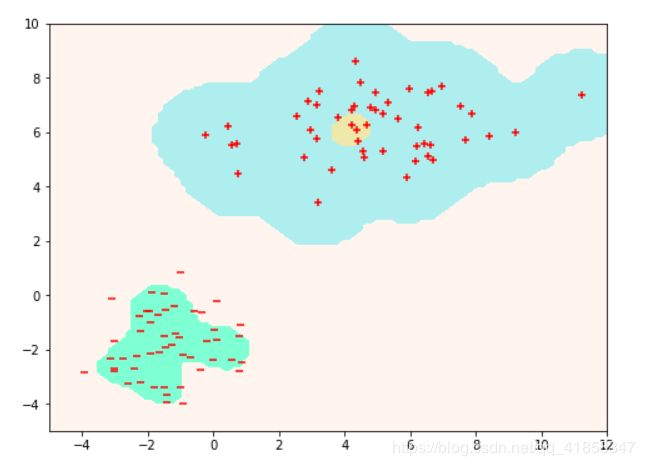
求解对偶问题的SMO算法比起传统优化方法获得的解是更稳定和高效的, 如果使用比上面更好的启发方法, 收敛将会更快(参考sklearn).

SVM优缺点和使用注意事项

优点

1. SVM是凸优化, 比神经网络的解更加稳定, 理论基础好.
2. 在高维数据上很高效(计算的本质是矩阵运算, 数据维度越高越易并行化, 类似神经网络)
3. 能处理非线性数据, 比线性分类器性能更好

缺点
4. 在大规模数据上不高效, 数据越大要考虑的alpha越多.
5. 不容易应用于多分类, SVM一般通过构造多个二分类器才能实现多分类, 而神经网络只需要单个模型.
6. 需要调参以防止核函数带来的过拟合

使用指南
7. 标准化数据, 把数据缩放到-1,1或0,1区间会让SVM更方便处理数据(尤其是多项式核)
8. 只保留一部分支持向量以减少内存的开销.
9. 在较多分类问题或极大规模数据里避免使用SVM
10. SVM对样本不平衡的敏感度很高, 可以尝试在SVM中添加数据的权重项来增强SVM在不平衡样本上的表现.

实践: 线性SVM分类乳腺癌样本

from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn import datasets

X,y = datasets.load_breast_cancer(return_X_y=True)

y = 2*y-1
# 我们设置较高的test_size来观察过拟合的发生
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size = 0.2, random_state = 1)

#数据标准化处理
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)

model = LibSVM(C = 5)
model.fit(torch.tensor(X_train).float(),torch.tensor(y_train).float(),max_iters = 1000)

y_pred = model.predict(torch.tensor(X_test).float()).numpy()
accuracy_score(y_pred, y_test)

0.9736842105263158

实践: 核SVM分类iris样本

class Multi_class_SVC:
    def __init__(self, num_class, C = 1, sigma = None):
        '''
        使用ovo的构造方式, 每两个类别之间构造一个二分类器
        '''
        self.num = num_class
        self.models = [[SVC(C = 1, sigma = None) for _ in range(i+1, num_class)]for i in range(num_class)]
        
    def fit(self, X, y, max_iters = 100):
        for i in range(self.num):
            for j in range(i+1, self.num):
                j_ = j-(i+1)
                indices_i = np.where(y==i)[0]
                indices_j = np.where(y==j)[0]
                data = np.concatenate([X[indices_i],X[indices_j]],axis = 0)
                labels = np.concatenate([
                    -np.ones(len(indices_i)),
                    np.ones(len(indices_j))],
                    axis = 0)
                self.models[i][j_].fit(data,labels,max_iters)
                
    def predict(self, x):
        '''
        采用投票制
        '''
        n = x.shape[0]
        votes = np.zeros((n,self.num))
        for i in range(self.num):
            for j in range(i+1, self.num):
                j_ = j-(i+1)
                y_pred_part = self.models[i][j_].predict(x).squeeze()
                indices = np.zeros(n).astype(np.int)
                indices[y_pred_part==-1] = i
                indices[y_pred_part==1] = j
                votes[range(n),indices] += 1
                
        return np.argmax(votes, axis = 1)

X,y = datasets.load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size = 0.2, random_state = 1)

model = Multi_class_SVC(3,C = 5)
model.fit(X_train,y_train,max_iters = 500)
y_pred = model.predict(X_test)
accuracy_score(y_pred, y_test)

1.0

备注

尽管上面的梯度下降是由torch自动求导得到的, 但是如果要自己手算导数也并不是困难的事情. 以kernel SVM的损失为例
$$\frac{\partial L}{\partial \alpha }=\frac{1}{2}(K\alpha +diag(K))-C(y_i{K}_{:j})if-y_i(\sum _{i=1}^N{\alpha }_{i}k(x,x_i)+b)+1\ge 0$$
$$\frac{\partial L}{\partial \alpha }=\frac{1}{2}(K\alpha +diag(K))if-y_i(\sum _{i=1}^N{\alpha }_{i}k(x,x_i)+b)+1<0$$
$$\frac{\partial L}{\partial b}=-C\ast y_{i}if-y_i(\sum _{i=1}^N{\alpha }_{i}k(x,x_i)+b)+1\ge 0$$
$$\frac{\partial L}{\partial b}=0if-y_i(\sum _{i=1}^N{\alpha }_{i}k(x,x_i)+b)+1<0$$