leetcode探索之初级算法篇——代码笔记整理

leetcode探索之初级算法篇——代码笔记整理

网址：https://leetcode-cn.com/explore/interview/card/top-interview-questions-easy/

本文对应的leetcode题目采取的写法为：<题号.题目名称> 例如：26.删除数组中的重复项

数组

26.删除数组中的重复项

双指针法，j前i后，初始时i=0.j=1；当a[i]与a[j]相同，j++；

a[j]与a[i]不同，i追上j的位置

int removeDuplicates(vector &nums)
    {
        if (nums.size() <= 1)
            return nums.size();
        int i = 0;
        for (int j = 1; j < nums.size(); ++j)
        {
            if (nums[i] != nums[j])
            {
                ++i;
                nums[i] = nums[j];
            }
        }
        return i + 1; 
        //return nums.size();//error 数组的后半部分没清理赶紧，因此需要返回i+1
    }

122.买卖股票的最佳时机

采取贪心算法，只要第二天价格高就卖出；

注意初始数组为空的情况

int maxProfit(vector& prices) 
    {
      int profit = 0;
        for(int i = 0; i + 1 < prices.size(); ++i) 
        {profit += max(prices[i + 1] - prices[i], 0);}
        return profit;
    }

189.旋转数组

旋转数组的低效写法是末尾出元素，开头入元素，舍弃；

高效写法的实质就是三次原地逆置数组，注意k值取模

void rotate(vector &nums, int k)
    {
        reverse(nums.begin(), nums.end() - k % nums.size()); 
        reverse(nums.end() - k % nums.size(), nums.end());
        reverse(nums.begin(), nums.end());
    }

217. 存在重复元素

存入set，用大小比较来巧妙解决是否有重复元素的元素；

注意每个分支if else后面都要有返回值，否则编译不通过

bool containsDuplicate(vector& nums) {
        sets1(nums.begin(),nums.end());
        return nums.size()!=s1.size();
    }

136.只出现一次的数字

遍历+异或 ，位操作无比高效

int singleNumber(vector& nums) {
       int result=0;
       for(auto elm:nums)
       {
           result^=elm;
       }
       return result; 
    }

350.两个数组的交集

运用哈希表来完成，一个数组负责加，一个数组负责减

	vector intersect(vector& nums1, vector& nums2) {
        vectorrec;
        unordered_mapmap;
        for(int i =0;i0)//两个数组有交集
           {
               rec.push_back(nums2[i]);
               map[nums2[i]]-=1;  //防止同一个数组中的重复元素的困扰
           }
        }
        return rec;
    }

66.加一

三种情况：

末尾无9，例如2548，直接++

末尾若干个9,例如299，9全变成0，第一个非9的数++

全部都是9，例如999，9全变成0，末尾添0，首位变成1

vector plusOne(vector &digits)
    {
        for (int i = digits.size() - 1; i >= 0; --i)
        {
            if (digits[i] == 9)
                digits[i] = 0;
            else
            {
                digits[i]++;
                return digits;
            }
        }
        digits.push_back(0);
        digits[0] = 1;
        return digits;
    }

283.移动零

遍历的时候，count记录零的个数，就地向前移动；

遍历结束之后，尾部count个元素令等于0；

以此实现原地改造数组

void moveZeroes(vector &nums)
    {
        int count = 0;
        for (size_t i = 0; i < nums.size(); ++i)
        {
            if (nums[i] == 0)
            {
                ++count;
            }
            if (nums[i] != 0)
            {
                nums[i - count] = nums[i];
            }
        }
        for (size_t i = nums.size() - 1; i > (nums.size() - count-1); --i)
        {
            nums[i] = 0;
        }
    }

1.两数之和

	vector twoSum(vector& nums, int target) {
        unordered_mapresult;
        vectorvec1;
        for(int i=0;isecond);
                break;
            }//could not find
            else result[nums[i]]=i;//insert 2,turn to 7,could find
        }
        return vec1;
    }

36.有效的数独

本题颇具难度，需要花点时间思考；

本解法仍待提升，希望采取哈希的写法提升效率

	int getSquare(int i,int j)
    {
        i=i/3;
        j=j/3;
        return i+3*j;
    }
    bool isValidSudoku(vector>& board) {
        vector> line(9, vector(10, 0));//共9行，每行10个数字对应0~9
		vector> row(9, vector(10, 0));//9列
		vector> square(9, vector(10, 0));//9个单元格
        for(int i=0;i<9;++i)
        {
            for(int j=0;j<9;++j)
            {
                if(board[i][j]=='.')
                {
                    continue;
                }
                int num=board[i][j]-'0';
                if(line[i][num]==0) {++line[i][num];}
                else return false;
                if(row[j][num]==0) ++row[j][num];
                else return false;
                if(square[getSquare(i,j)][num]==0)  ++square[getSquare(i,j)][num];
                else return false;
            }   
        }
            return true;
    }//没有用哈希，因此效率不够好

48.旋转图像

实质是原地旋转90度，仔细观察规律
1.沿主对⻆角线所有元素交换
2.沿着垂直中轴线⽅方向所有元素交换

void rotate(vector>& matrix) {
	for(int i = 0; i < matrix.size(); i++)
		for(int j = 0; j <= i; j++)
			swap(matrix[i][j], matrix[j][i]);
	for(int i = 0, j = matrix.size() - 1; i < j; i++, j--)
		for(int k = 0; k < matrix.size(); k++)
			swap(matrix[k][i], matrix[k][j]);
}

---

字符串

344.反转字符串

遍历时引入temp交换即可

void reverseString(vector& s) {
        char temp;
        int size = s.size();
        for(int i=0;i

7.整数反转

原生反转其实很简单，三句话就可实现

在防溢出这里的写法是值得学习的

   //INT_MAX = 2^31-1=2147483647；
   //INT_MIN= -2^31=-2147483648；

	int reverse(int x) {
        int ret=0;
        while(x!=0)
        {
            int pop=x%10;
            x/=10;
            if(ret>INT_MAX/10||(ret==INT_MAX/10&&pop>7))return 0;
            if(ret

387.字符串中的第一个唯一字符

两次遍历，遍历的精髓就在以数组下标i为变化量，两次都是以i来遍历，因为返回值是数组下标

	int firstUniqChar(string s) {
        mapmp1;
        int length=s.size();
        for(int i=0;i

242.有效的字母异位词

两个字符串，一个负责“加”，一个负责“减”

	bool isAnagram(string s, string t) {
         if(s.size() != t.size())
            return false;
        int *alpha = new int[26](); //只包括小写字母
        for(int i = 0; i< s.size(); i++) {
            alpha[s[i] - 'a'] ++;
            alpha[t[i] - 'a'] --;
        } //如果数目完全相同，则alpha所有位值都是0，一加一减的方法很巧妙
        for(int i=0;i<26;i++){
            if(alpha[i] != 0)
            {return false;}
        }
        return true;
    }

125.验证回文字符串

回文的特性决定了双指针的写法，一个从前往后一个从后往前

while内部的用法很细节，isalnum tolower很细节，把不纳入判断的元素过滤

	bool isPalindrome(string s) {
        // 双指针
        if(s.size() <= 1) return true; //空字符串返回true
        int i = 0, j = s.size() - 1; //一个头一个尾
        while(i < j){
            while(i < j && !isalnum(s[i])) 
            // 如果是合格字符，while（0）直接跳过，最后到了比对环节；如果是非合格字符，如逗号，while（1）执行i++，跳过了这个非字符元素，
            {
                i++;
            }
            while(i < j && !isalnum(s[j]))
            {
                j--;
            }
            if(tolower(s[i++]) != tolower(s[j--])) 
            //统一转换成小写字母再比较，比对环节一旦出问题，直接return false；
                return false;
        }
        return true;
    }

8.字符串转换整数 (atoi)

这道题目细节之处很多，代码值得仔细研究

	int myAtoi(string str) {
        int ret=0;
        int i=0;
        int flag=1;
        while(str[i]==' ')
        {
            ++i;
        }
        if(str[i]=='-')
        {
            flag=-1;
        }
        if(str[i]=='+'||str[i]=='-')
        {
            ++i;
        }
        //数字处理这里十分细节
        while(iINT_MAX/10||(ret==INT_MAX/10&&r>7))
            {
                return flag>0?INT_MAX:INT_MIN;
            }
            ret=ret*10+r;
            ++i;
        }
        return flag>0?ret:-ret;
    }

28.实现strstr()

最暴力的解法是粗暴回退法，KMP是其改进

对于solution里的KMP和dp KMP还需要钻研

vector getnext(string str)
        {
            int len=str.size();
            vector next;
            next.push_back(-1);
            int j=0,k=-1;
            while(j next;
        next=getnext(needle);
        while((i

38.外观数列

递归和出口、count计数、字符串拼接

	string countAndSay(int n) {
        if(n==1) return "1";
        string strlast=countAndSay(n-1);
        int count=1;
        string ret;
        for(int i=0;i

14.最长公共前缀匹配

先遍历，找到最短的字符串；再遍历最短字符串的每一个元素，如果和其他的相同位置元素不匹配，直接return false；全部匹配返回true；

	string longestCommonPrefix(vector& strs) {
        string ans = "";
        if(strs.empty())    return ans; //输入为空，输出空ans
        int arr = strs.size();
        string min = strs[0];
        for(int i = 1; i < arr; ++ i) //找到最短字符串
        {
            if(strs[i].size() < min.size())
                min = strs[i];
        }
        for(int j = 0; j < min.size(); ++ j) 
        //从第一个字符开始对比，若都一样，ans加上该字符，若不一样，返回答案；
        {
            for(int m = 0; m < arr; ++m)
            {
                if(min[j] != strs[m][j])
                    return ans; //错误就直接返回
            }
            ans = ans + min[j]; //全部对上了就把内容加上
        }
        return ans;
    }

---

链表

237.删除链表中的节点

很简单，略过，不断链即可

 void deleteNode(ListNode* node) { //已经定义好了这个ListNode结构体，并且把要删除的结点传了进来
        *node=*(node->next);
    }

19.删除链表的倒数第N个节点

双指针法是链表中常用的技术手段

	ListNode* removeNthFromEnd(ListNode* head, int n) {
        //如果用两次遍历法，也应该先创建个头结点
        ListNode* former=new ListNode(0);
        former->next=head;//这次尝试双指针法
        ListNode * p=former;
        ListNode * q=former;//这里都要从former开始,避免了初始1个元素就删除这一个元素的情况
        int count=0;
        while(countnext;
        } //先把p q偏移好一定的位置
        while(q->next!=NULL)
        {
            q=q->next;
            p=p->next;
        }//p q 一起右移，直到q移到最后一个元素位置
        ListNode * del=p->next;//写这步的目的是del删除节点，回收资源。否则直接双next写法
        p->next=del->next;
        delete del;
        ListNode * ret=former->next;
        delete former;
        return ret;
    }

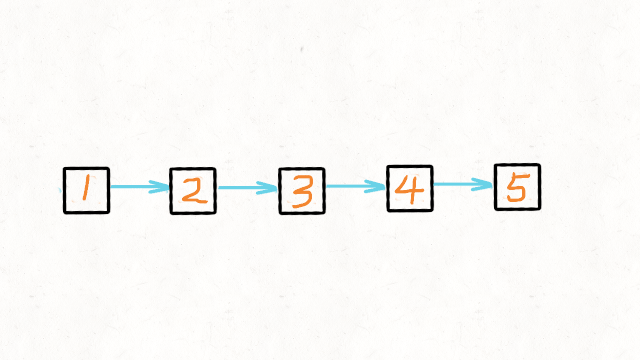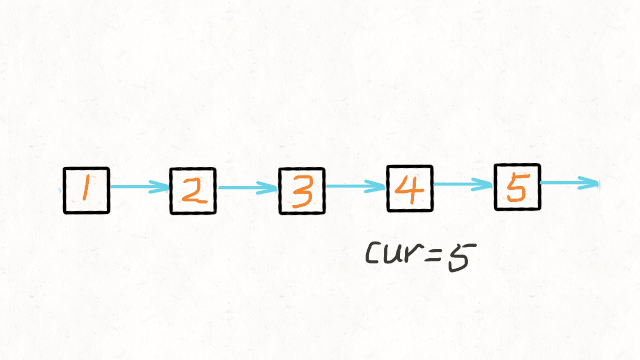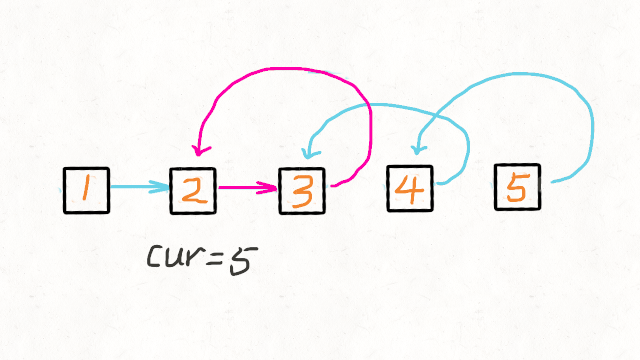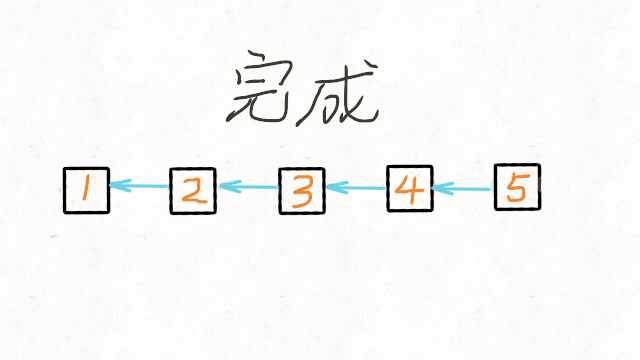
206.反转链表

递归的写法，如图

一次遍历，边遍历边修改的写法是最好

	ListNode* reverseList(ListNode* head) {
        if(head==nullptr)
        {
            return head;
        }
        ListNode * first = head;
        ListNode * target = first->next;
        while(target!=nullptr)
        {
            first->next=target->next;
            ListNode * temp = target->next;
            target->next=head;
            head=target;
            target=temp;
        }
        return head;
    }

21.合并两个有序链表

精髓思想是，不改变原有的两个链表的本来指向，新定义一个指针，规定其指向，不断把满足要求的结点添加到其后面

	ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode * former = new ListNode(-1);
        ListNode * curnode = former;
        while(l1!=nullptr&&l2!=nullptr)
        {
            if(l1->val>l2->val)
            {
                curnode->next=l2;
                l2=l2->next;
            }
            else
            {
                curnode->next=l1;
                l1=l1->next;
            }
            curnode = curnode -> next;
        }
        curnode->next= l1==nullptr ? l2:l1;
        return former->next;
    }

234.回文链表

尝试用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题，待参考柳婼的解法来补充完整

141.环形链表

set容器存储指向结点的指针，遍历这个容器，找得到则有环，找不到则无环

	bool hasCycle(ListNode *head) {
        if(head==nullptr||head->next==nullptr)
        {
            return false;
        }
        setnodeset;//set容器内部装指针
        while(head->next!=nullptr)//遍历
        {
            if(nodeset.count(head)!=0)//有这个节点，直接就是环了
            {
                return true;
            }
            else{
                nodeset.insert(head);//没有这个节点就插入
            }
            head=head->next;
        }
        return false;//遍历完以后，都没有这个节点，就是没有环
    }

---

树

树的操作常用到递归和迭代的写法，这和树的特性有关；递归的效率比较低，如果可以改进写法，效率能够提升

104.二叉树的最大深度

左右各一个遍历记录值，递归+=，返回最大值

	int maxDepth(TreeNode *root)
    {
        if (root == nullptr)
            return 0;
        //用递归来写
        int depth_l = 1;
        int depth_r = 1;
        depth_l += maxDepth(root->left);
        depth_r += maxDepth(root->right);
        return depth_l > depth_r ? depth_l : depth_r;
    }

98.验证二叉搜索树

利用二叉搜索树满足的特性：

中序遍历存数据进入vec数组，对数组遍历看是否是升序，是则合格

 	void inorder(TreeNode * root,vector& vec)
    {
        if(root==NULL)return ;
        inorder(root->left,vec);
        vec.push_back(root->val);
        inorder(root->right,vec);
    }
    bool isValidBST(TreeNode* root) {
        vectorvec;
        inorder(root,vec);
        for(int i=1;i

101.对称二叉树

总函数 isSymmetric借助辅助函数 helper，辅助函数内部写好边界再递归，这样的设计思想需要学习

 	bool helper(TreeNode * l , TreeNode * r)
    {
        if(l==NULL&&r==NULL) return true;
        if(l==NULL||r==NULL) return false;
        if(l->val!=r->val) return false;
        return helper(l->left,r->right)&helper(l->right,r->left); //这句话是精髓
    }
    
    bool isSymmetric(TreeNode* root) {
        if(!root) return true;
        return helper(root->left,root->right);
    }

102.二叉树的层次遍历

用数组vector和队列queue解决

队列牢牢地掌控了层次遍历的顺序

vector为了vector服务

vector> levelOrder(TreeNode *root)
    {
        vector row;
        vector> ret;
        queue que;
        if (root == NULL)
            return ret;
        TreeNode *temp;
        que.push(root);
        while (!que.empty())
        {
            int size = que.size();
            while (size--) //把同一层的放到一起
            {
                temp = que.front(); //先留个号码，好找
                que.pop();          //再出队
                row.push_back(temp->val);
                if (temp->left != NULL)
                {
                    que.push(temp->left);
                }
                if (temp->right != NULL)
                {
                    que.push(temp->right);
                }
            }
            ret.push_back(row);
            row.clear();
        }
        return ret;
    }

108.将有序数组转换为二叉搜索树

核心在于有序数组的中间值是根节点，代码虽短，细节不少

TreeNode* sortedArrayToBST(vector& nums) {
        if(nums.empty()) return nullptr;
        return helper(nums,0,nums.size()-1);
    }

    TreeNode * helper(vector&nums,int left,int right)
    {
        if(left>right)
        {
            return nullptr;
        }
        int mid=(left+right)/2; //升序的有序数组变成平衡二叉树，根节点一定在中点的位置
        TreeNode * root = new TreeNode(nums[mid]);
        root->left=helper(nums,left,mid-1);
        root->right=helper(nums,mid+1,right);
        return root;
    }

---

排序和搜索

88.合并两个有序数组

几个边界，写错了两次，需要多注意

	void merge(vector& nums1, int m, vector& nums2, int n) {
        if(!m) {
            swap(nums1,nums2);
            return;
        }
        if(!n){
            return;
        }
        int k1=m-1;
        int k2=n-1;
        int k3=n+m-1;
        while(k1>=0&&k2>=0)
        {
            //前面是判断，后面是执行
            nums1[k3--]=nums1[k1]>nums2[k2]?nums1[k1--]:nums2[k2--];
        }
        while(k2>=0)
        {
            nums1[k3--]=nums2[k2--];
        }//避免nums1走完，nums2没走完的情况
    }

278.第一个错误的版本

二分查找法，可以通过递归和迭代两种方式实现

	int firstBadVersion(int n) {
        //第一直觉是写一个二分查找
        int left=1;
        int right=n;
        while(left

---

动态规划

70.爬楼梯

如何爬上第n节台阶？可以由第n-1节爬一格上来，也可以由n-2节爬2格子上来

方针：“借助过去，实现现在”

	int climbStairs(int n) {
        int * a = new int[n+1];
        a[0]=1; //把n从0开始的所有情况，涵盖了进来
        a[1]=1;
        for(int i=2;i<=n;++i)
        {
            a[i]=a[i-1]+a[i-2];
        }
        return a[n];
    }

121.买卖股票的最佳时机

一次遍历实现，之前记录的profit为现在的ret提供了参考

int maxProfit(vector& prices) {
        int ret = 0;
        int profit;
        int minpr=99999;
        for(int i=0;i

53.最大子序和

之前的累加值为现在的选择做出了参考

	int maxSubArray(vector& nums) {
        int len = nums.size();
        if(len==0) return 0;
        int ans = nums[0] ;
        int temp = nums[0];
        for(int i=1;i0){
                temp=temp+nums[i]; //累加值存在temp中，当temp为正，无条件往后累加
            }else{
                temp=nums[i]; //之前的累加值为负，证明是失败的，重新赋予新的累加值temp
            }
            ans=max(ans,temp); //只返回历史中最大的那个累加值
        }
        return ans;
    }

198.打家劫舍

充分体现动态规划记录数据特性的一道题，解法值得推敲

	int rob(vector& nums) {
        int n = nums.size();
        if(!n) return 0;
        if(n==1) return nums[0];
        //以三个元素举例，房子1小于房子2价格，现在来到了房子3
        int curmax=0;//房子2价格
        int premax=0;//房子1价格
        for(int x:nums)
        {
            int temp=curmax;
            curmax=max(curmax,(premax+x));
            premax=temp;
        }//三个int型数据完成全部内容
        return curmax;
    }

---

设计问题

关于设计的这两道题，自己需要加类的成员函数，加类的私有对象

384.打乱数组

涉及到数组的提前保存和随机数的取得，随机数取得后与还未出场的数进行交换

class Solution {
private:
    vector_nums;
    vector_origin;
    
public:
    Solution(vector& nums) {
        this->_nums=nums;
        this->_origin=nums;
    }
    
    /** Resets the array to its original configuration and return it. */
    vector reset() {
        return this->_origin;
    }
    
    /** Returns a random shuffling of the array. */
    vector shuffle() {
        int len=_nums.size();
        if(!len) return _nums;
        for(int i=len-1;i>=0;--i)
        {
            int random = rand()%(i+1);
            swap(_nums[random],_nums[i]);
        }
        return _nums;
    }
};

155.最小栈

借用辅助栈来实现以空间换时间

class MinStack {
private:
    stacksta;
    stackmin;


public:
    void push(int x) {
        sta.push(x);
        if(min.empty()||x<=min.top()) //=防止出现连续两个最小的-10
        {
            min.push(x);   
        }
    }
    
    void pop() {
        if(sta.top()==min.top())
        {
            min.pop();
        }    
            sta.pop();
    }
    
    int top() {
        return sta.top();    
    }
    
    int getMin() {
        return min.top();
    }
};

---

数学

412.Fizz Buzz

数学问题，对症下药

	vector fizzBuzz(int n)
    {
        vector ret;
        for (int i = 1; i <= n; ++i)
        {
            if (i % 15 == 0){
                ret.push_back("FizzBuzz");
                continue;
            }
            if (i % 3 == 0 ){
                ret.push_back("Fizz");
                continue;
            }
            if (i % 5 == 0 ){
                ret.push_back("Buzz");
                continue;
            }
            else
            {
                ret.push_back(to_string(i));
            }
        }
        return ret;
    }

204.计数质数

关于质数，有个很神奇的筛法，叫**“厄拉多塞筛法”**

核心思想是，当一个数确定为质数后，它的倍数全部都不会是质数，筛掉

	int countPrimes(int n) {
        int count=0;
        vectorvec(n,true);
        for(int i=2;i

优化操作：用bitmap对筛选算法进行内存优化

int countPrimes(int n) {
    int count = 0;
    //一个 int 变量不知道占多少字节（但请注意，这里采用了常量）
    const int size = sizeof(int) * 8;
    vector signs(n / size + 1,0);
    for (int i = 2; i < n; i++){
        //将元素和需确定得数字经行按位或运算，如果值改变，说明不存在该数字（未登记该数字），则其为质数。
        //在C++中，其提供了 bitset 来操作位，在此便不做介绍了。如果用了，可读性肯定会更好。
        //(当某个数为 2 的 n 次方时（n为自然数），其 & (n - 1) 所得值将等价于取余运算所得值)
        //*如果 x = 2^n ，则 x & (n - 1) == x % n
        //下面判断可以写成
        //if ((signs[i / size] & (1 << (i % 32))) == 0)
        if ((signs[i / size] & (1 << (i & (size - 1)))) == 0){
            count++;
            for (int j = i + i; j < n; j += i){
                //登记该数字
                signs[j / size] |= 1 << (j & (size - 1));
            }
        }
    }
    return count;
}

326. 3的幂

有很多迭代和递归的写法，这里提供的是非循环和迭代的写法，更为优秀

class Solution {
	public:
	bool isPowerOfThree(int n) {
	if(n <= 0) return false;
	return pow(3, (round)(log(n) / log(3))) == n; //如果是3的幂次，一定是整数次幂
	}
};

13.罗马数字转整数

要点：pair的用法 || 罗马数字摆放的本质规律

	int romanToInt(string s) {
        int ans=0;
        mapmp;
        char roman[]={'I','V','X','L','C','D','M'};
        int val[]={1,5,10,50,100,500,1000};
        for(int i=0;i<7;++i)
        {
            mp.insert(pair(roman[i],val[i]));
        }
        for(int i=0;i=mp[s[i+1]]){
                ans+=mp[s[i]];
            }
            else{
                ans-=mp[s[i]];
            }//成功解决IX类型写法，看透了本质
        }
        ans+=mp[s[s.size()-1]];
        return ans;
    }

---

其他

191.位1的个数

涉及到“位bit”，与或非操作不可忘！

迭代法是基础

	int hammingWeight(uint32_t n)  //传进来的是32位的2进制数
    { 	
        int ret = 0;
        uint32_t mask = 1;
        for (int i = 0; i < 32; ++i)
        {
            if ((n & mask) != 0)
            {
                ++ret;
            }
            mask = mask << 1;
        }
        return ret;
    }

461.汉明距离

实质是找出有几个位是不同的，异或、与操作、算术右移

	int hammingDistance(int x, int y) {
        int count=0;
        int xor1=x^y;//异或后，不同的位留下的都是1
        while(xor1>0)
        {
            if(xor1&1==1)//把所有的1数出来，用与的方法
            {
                ++count; 
            }
            xor1>>=1; //算术右移一位
        }
        return count;
    }

190.颠倒二进制位

pop || x || ret 经典搭配，实现 逆置一个数

	uint32_t reverseBits(uint32_t n) {
        uint32_t ret = 0;
        uint32_t pop = 0;
        for(int i=0;i<32;++i){
            pop=n%2;
            n=n/2;
            ret=ret*2+pop;
        }
        return ret;
    }

118.帕斯卡三角/杨辉三角

考察vector创建二维数组的操作，需要多练

vector> generate(int numRows) {
	vector> v(numRows);
	if(numRows == 0) return v;
	for(int i = 0; i < numRows; i++) {
		v[i].resize(i + 1);
	}
	v[0][0] = 1;
	if(numRows == 1) return v;
	v[1][0] = 1;
	v[1][1] = 1;
	for(int i = 2; i < numRows; i++) {
	v[i][0] = 1;
	v[i][i] = 1;
	}
	for(int i = 2; i < numRows; i++) {
		for(int j = 1; j < i; j++) {
			v[i][j] = v[i - 1][j - 1] + v[i - 1][j];
		}
	}
	return v;
}

20.有效的括号

核心是栈的入栈和出栈

	bool isValid(string s) {
       stacksta;
       int len = s.size();
       if(!len) return true;
       if(len%2==1) return false;//先把边界条件写好
       for(int i=0;i

268.缺失数字

观察规律，然后解决

代码里写了两种遍历方式，后者效率更高

	int missingNumber(vector& nums) {
        int len=nums.size();
        int total=(0+len)*(len+1)/2;
        for(int x : nums)
        {
            total-=x;
        }
        // for(int i=0;i