深度学习 | 模型评估与梯度下降优化

————————————————————————————
原文发表于夏木青 | JoselynZhao Blog，欢迎访问博文原文。
————————————————————————————

深度学习教程与实战案列系列文章

---

深度学习 | 绪论
深度学习 | 线性代数基础
深度学习 | 机器学习基础
深度学习 | 实践方法论
深度学习 | 应用
深度学习 | 安装conda、opencv、pycharm以及相关问题
深度学习 | 工具及实践（TensorFlow）
深度学习 | TensorFlow 命名机制和变量共享、变量赋值与模型封装
深度学习 | TFSlim介绍
深度学习 | TensorFlow可视化
深度学习 | 训练及优化方法
深度学习 | 模型评估与梯度下降优化
深度学习 | 物体检测
深度学习| 实战1-python基本操作
深度学习 | 实战2-TensorFlow基础
深度学习 | 实战3-设计变量共享网络进行MNIST分类
深度学习 | 实战4-将LENET封装为class，并进行分类
深度学习 | 实战5-用slim 定义Lenet网络，并训练测试
深度学习 | 实战6-利用tensorboard实现卷积可视化
深度学习 | 实战7- 连体网络MINIST优化
深度学习 | 实战8 - 梯度截断
深度学习 | 实战9- 参数正则化

---

机器学习与模型优化选择

机器学习是一个怎样的过程?

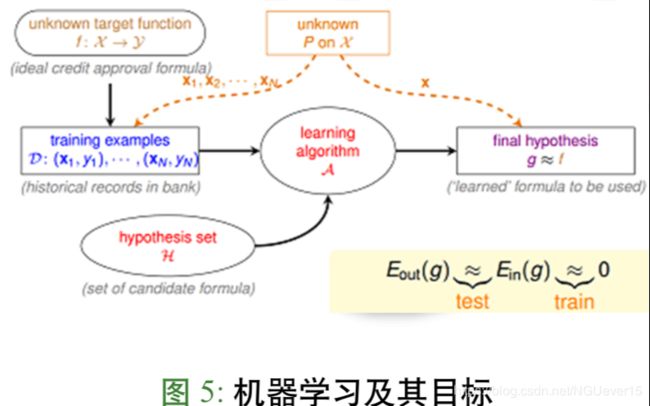
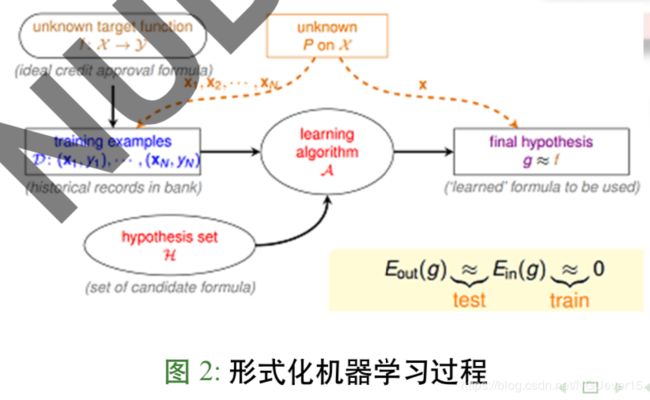
形式化机器学习过程

机器学习是一个模型选择过程

机器学习:通过算法 A，在假设空间 H 中，根据样本集 D，选择最优假设 g。选择标准: g 近似于 f

• f :理想映射 g :机器学习结果，输出映射 g ∈ H
• H :机器学习的假设空间 Hypothesis space: “defines the class of functions mapping the input space to the output space. ”(李铁岩”Learning to Rank for Information Retrieval”. P16)
• 假设空间 H 的确定意味着学习范围的确定
• 学习目的:找到 H 中最优的模型 g(H 一定，则 g 是相对的最优)
  

机器学习要素

• 机器学习:从训练数据，应用评价准则，从模型假设空间中选取一个最优的模型
• 机器学习是一个模型选择过程 模型假设空间(优化对象):形式，结构，超参数，参数
• 评价准则(优化目标):选择模型的标准:经验风险最小?结构风险最小?综合?。
  

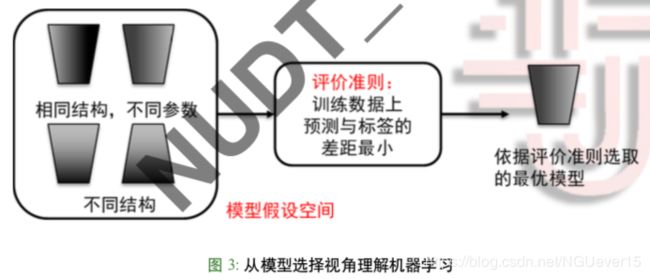
评测是用来挑选最优模型的

学习优化对象:模型假设空间的元素

• 模型假设空间 H:模型形式及其参数
• 例:(1) 一组不同的映射,H 空间组成: 映射 + 参数
• (2) 确定的映射关系, H 空间组成: 参数 $h(\theta ;x)={\theta }_0+{\theta }_{1}x$

学习优化目标:降低泛化误差

泛化误差Eout 指的是在“未来”样本上的误差
经验误差Ein 指的是在训练集上的误差，也称为“训练误差”

泛化目标分解

1. Ein（h）≈ 0：如何降低经验误差
2. Eout(h) ≈ Ein(h):如何 保证泛化能力
   

降低 Ein(h) : 机器学习优化过程

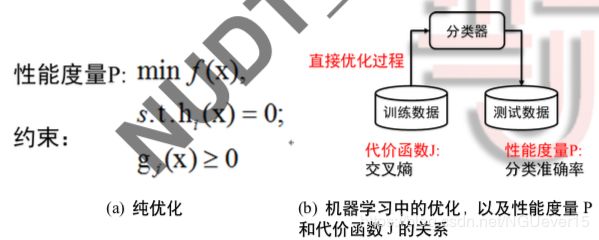
机器学习与纯优化的区别和联系

• 纯优化:给定约束下，寻找某些变量，使指标 P 达到最优
• 机器学习:性能度量 P(直接评价准则)定义于测试集，并且可能不可解。往往通过降低代价函数 J(间接评价准则)，来间接的降低 P。
• 给定模型假设空间和评价准则后，在训练数据上的寻优过程是一种直接优化过程

确保泛化性能 Ein(h) ≈ Eout(h):机器学习的可学习问题

优化之外的问题

泛化性能由学习算法的能力、数据的充分性以及学习任务本身的难度 共同决定
任务复杂度 → 足量数据表达 → 足够复杂模型学习
给定假设空间是否可学到有效模型?
任务难度无法控制
**可以控制的因素:**数据量 N, 模型复杂度 M((或有效假设数，或模型容 量)

模型选择

泛化误差来源

泛化误差分解

泛化性能由学习算法的能力、数据的充分性以及学习任务本身的难度共同决定

泛化误差来源

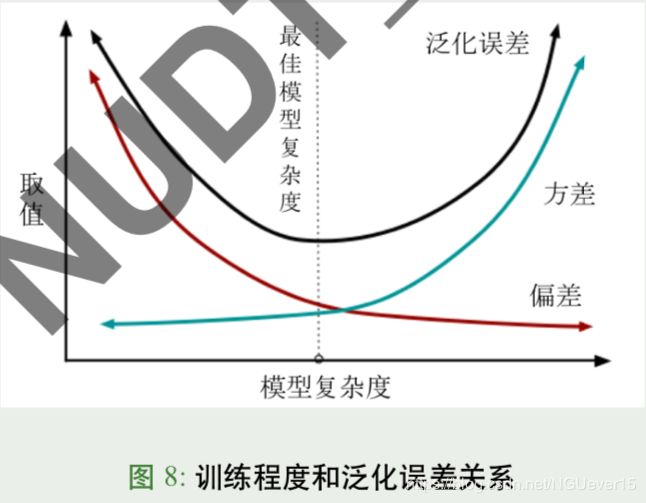
训练程度对泛化误差影响

一般而言，偏差与方差存在冲突

• 训练不足时，学习器拟合能力不强，偏差主导

• 随着训练程度加深，学习器拟合能力逐渐增强，方差逐渐主导
  

• 训练充足后，学习器的拟合能力很强，方差主导
  

• 可见，偏离中心的方差成为泛化误差主要来源，其本质又是什么?
  

图解: 模型复杂度太低 会 导致学习器拟合能力不强，此时方差小，偏差占主导
模型复杂度高时，使得学习器集合能力强（过拟合），方差主导。 （模型复杂度过高会导致过拟合）

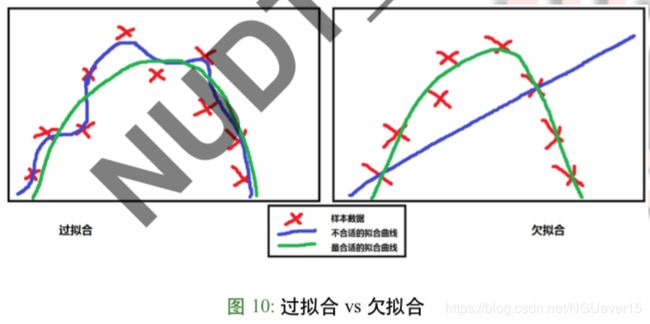
过拟合 vs 欠拟合

模型选择，纯优化之外的问题

模型经过样本充分训练，依然存在的问题

• 过拟合，overfitting 模型将训练样本的特殊性质当作了未来样本的一般性质，导致很大的方差误差， 泛化性能下降
  特点:训练精度高，测试精度低:Ein(h) ≈ 0 Eout(h)↑
• 欠拟合，under-fitting 与过拟合相对应，模型不能表达训练样本的一般性质，偏差本身就很大特点:训练精度和测试精度都不高:Ein (h)↑ Eout (h)↑
  

模型选择关系学习成败

模型经过样本充分训练，依然存在的问题

• 过拟合，overfitting 本质:模型相对任务过于复杂
• 欠拟合，under-fitting 本质:模型相对简单，已相对数据饱和，再多数据也没用
  

模型评估:经验误差 Ein(h) 和泛化误差 Eout(h) 的距离

模型有效假设数 M 和数据量 N 对泛化误差的影响

? 什么叫有效的不同映射个数？
妈呀，这页看不懂

VC dimension 与模型复杂度

如果 VC Dimension 太大，模型复杂度增加，E-in 与 E-out 偏离 (过 拟合)
如果 VC Dimension 太小，虽然 E-in≈E-out，但 H 不够给力，很难 找到不犯错(或很少犯错)的 h(欠拟合)

模型复杂度对应数据量举例

例:用模型的 VC Dimension = 3 的模型做分类，要求 E-in 与 E-out 差 距最大为 ε=0.1;置信度为 90

理论上:need N ≈ 10000 * VC Dimension
实际应用:need N ≈ 10* VC Dimension
因为 VC Bound 过于宽松，是一个比实际大得多的上界

神经网络 VC 维估计

• 对于神经网络:粗略估计: dVC = O(VD)，
• V: 神经网络中神经元的个数，D:weight 的个数，也就是神经元之间连 接的数目。
  (注意:深度神经网络目前没有明确的 vc bound)
• 举例:一个普通的三层全连接神经网络:input layer 是 1000 维，hidden layer 有 1000 个 nodes，output layer 为 1 个 node，则它的 VC 维大约为 O(100010001000)
• 三层全连接神经网络，VC 维大约为 O(100010001000)
• 实际应用中至少需要 10 倍数据
• 卷积网络的优势:大量权值共享，减小了 VC 维度

模型选择

模型选择原则

• 奥卡姆剃刀原理:
  同样效果情况下，选简单的
• 没有免费午餐 No Free Lunch Theorems: 没有哪个算法比其他算法在任何任务下都绝对高效 某个模型在某个任务下有效，在另一个任务中可能就会差些 根据具体问题，选择合适任务的模型假设

评估方法和评估指标

模型评估

模型评估的目的和要素

• 机器学习:反复迭代 (模型假设 =⇒ 训练优化 =⇒ 性能评估)
• 评估目的:通过一定测试方法，反映模型在未来应用数据上的泛化能力
• 评估要素:评估方法、评估指标
• 一般方法: 选取部分数据为测试集，代表未见数据，用相应指标测试泛化性能
• 常见数据划分方式:
  训练集 (training):用于训练模型，优化模型参数
  验证集 (validation)(可选):用于训练中的调参效果评估
  测试集 (test):模型效果最终依据
• 数据划分要求:各个数据集相互互斥独立;每个数据集上的数据分布都应尽量符合任务数据分布

评估方法

测试集选取方法

• 如前所述，评估方法常用设置测试集的方式
• 关键:如何获得“测试集”(test set)
• 原则:测试集与训练集应该“互斥”;尽量与数据分布一致
• 常见方法:
  留出法(hold-out)
  交叉验证法(cross validation)
  自助法（bootstrap）

留出法

“留出法”直接将数据集 D 划分为两个互斥的集合，其中一个集合作为 训练集，另一个作为测试集。

注意:

• 保持数据分布的一致性(例如:保留类别比例的分层采样)
• 多次重复划分(例如:100 次随机划分)
• 测试集不能太大或太小(例如:1/5 1/3) 大了:训练集小，训练不充分;小了: 难以表达数据分布，测试不充分

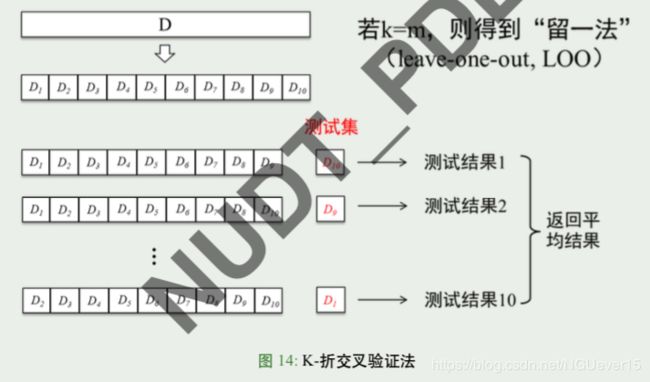
K-折交叉验证法

自助法

• “自助采样”(bootstrap sampling)，亦称“有放回采样”、“可重复采样”
• 从 m 个样本的总数据集 D 中，通过采样生成训练集 D’
• 测试集为 D/D’(亦称包外估计 out-of bag estimate)
• 采样 m 次:每次从 D 随机采一个 d 放入 D’, 再将 d 放回 D
• 大数下约有:limm→∞ (1−1/m)m → 1/e ≈ 0.368 的样本不出现在 D’ 中
  
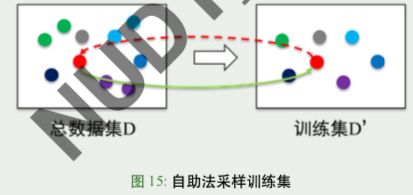
  优点:适用于小数据集;可生成不同的训练集

评估指标

模型的性能度量

• 性能度量 (performance measure): 衡量模型泛化能力的评价标准
• 什么样的模型是“好”的，不仅取决于算法和数据，还取决于任务需求
• 不同任务，也倾向不同的评价标准，归结为一些列评价指标
• 常用的评价指标
  • 错误率与精度
  • 查准率，查全率，F1, P-R 图
  • ROC 与 AUC
  • 代价敏感错误率与代价曲线

错误率 vs. 精度

精度可以理解为正确率

问题:当正负样例在数据集中严重失衡时，会使得这种度量方式缺乏说服力。

例如生物信息学中的基因剪辑点的识别任务中，正样例的占比可能只有万分之一，那么 假设有一个无效模型，把所有的样例都分类为负样例，这样它的错误率会小于 0.01%， 而精度会高于 99.99%，但这个模型显然是无效的。

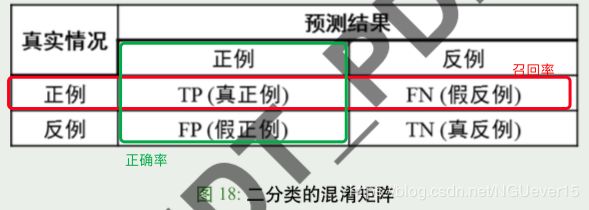
混淆矩阵 (confusion matrix)

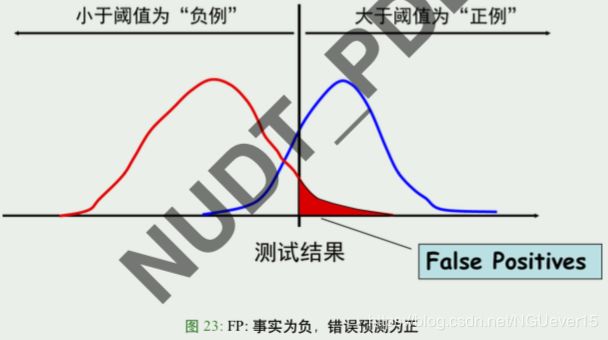
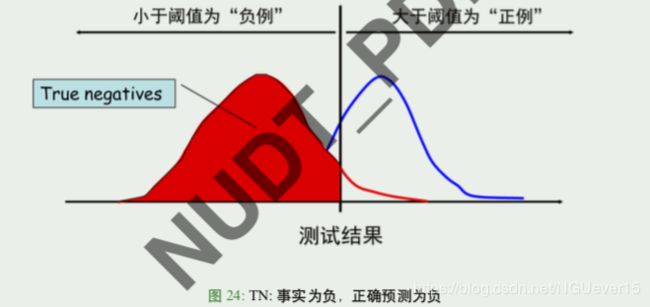
对于二分类问题，可将样例根据其真实类别与学习器预测类别的组合划分为真正例 (true positive)、假正例 (false positive)、真反例 (true negative)、假反例 (false negative) 四种情形 由此定义二分类结果的“混淆矩阵”(confusion matrix）如下：

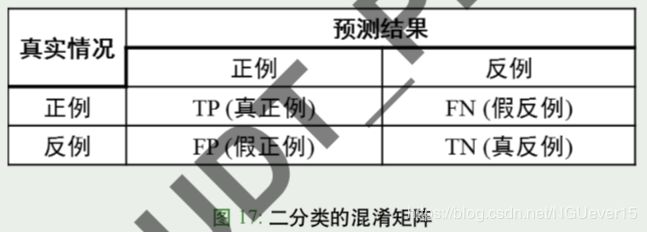
对于多分类，也可构造类似混淆矩阵，此时表头行、列分别表示各类预测 (prediction) 与 各类真实值 (ground truth)
怎样好记?T,F,P,N 都是在修饰预测结果

前缀:”T” 真，就是正确预测，”F” 假，就是错误预测;
后缀:”P” 就是预测成正例，”N” 就是预测成反例
例如:FN: 错误预测成反例 (也就是把正例预测为反例）

查准率(精度)、查全率(召回率)

查准率（精度）是 正确预测的 正例 / 所有对正例的预测
查全率（召回率） 是 正确预测的 正例 / （正确预测的正例+ 错误预测的反例）

在目标检测中，人脸识别等应用中，这两个指标我们关心比较多：

• 精度 precision:预测是 A 类的结果里到底有多少是 A, 精度低，说明 “虚警”高
• 召回率 recall:实际样本里的 A 类有多大比例被争取识别为 A, 召回
  率低，说明“漏检”多

P-R 曲线,AP 值与 BEP 盈亏平衡点

很多模型的应用，需要设置额外的参数或阈值:例如二分类的阈值，目标检测的 IoU 等 不同的模型的比较，应该比较不同参数、阈值下的综合性能

综合性能评测:模型针对不同参数、阈值等得到的预测结果，可按查准率(精度)、查全 率 (召回率)作为点坐标，在平面上绘出一条 P-R(Precision-recall) 曲线

不同模型的 P-R 曲线比较:**P-R 曲线下方包裹面积:AP(Average precision);AP 大，性能 更高;**对于多分类问题，实际每一类有一条 P-R 曲线，此时综合性能用 mAP(mean Average precision) 衡量，即是各类的 AP 的平均值

不同 PR 曲线交叉时，还可参考 BEP 盈亏平衡点的高低，判断模型性能
BEP 盈亏平衡点: 曲线上，查准率(精度)= 查全率 (召回率)的点

F1 score

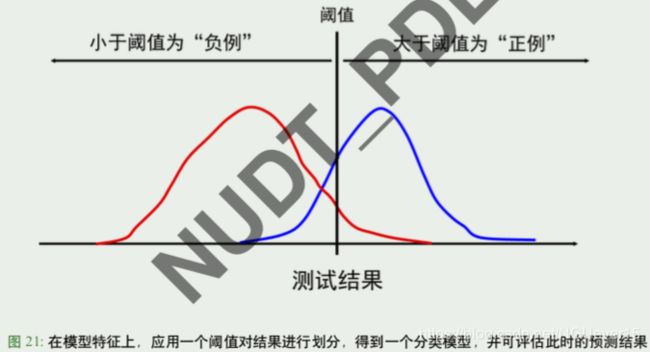
ROC 曲线

P-R 曲线是以正例为中心的评价方式，事实很多应用 (例如人脸识别)，我们关心正例 (两 张照片是同一个人) 和反例 (两张照片不是一个人) 都有同样高的精度

ROC (Receiver Operating Characteristic) 曲线，与 P-R 图类似，纵轴是“真正例率”(True Positive Rate，TPR) ，横轴是“假正例率”(False Positive Rate，FPR)，其意义为:

因此，ROC 曲线并不是 P-R 曲线反过来画 (x’=1-x) 的结果 理想的结果应该:TPR 高，说明正例漏检少，FPR 低，说明反例误检低

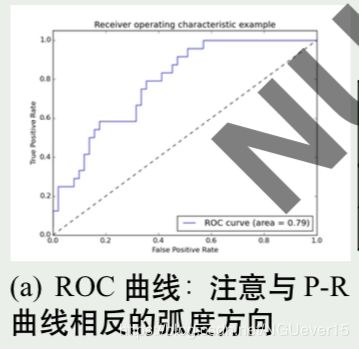
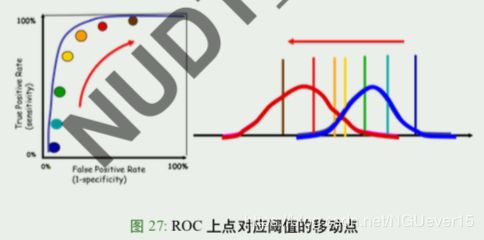
ROC 上点和阈值点的对应关系

随着阈值向左移动 (右为正例，左为负例) 正例被正确检出的比例不断增大，y 值增大, 但到所有正例全被检出时 (y=1)，停止增长
而事实反例中被误检为正例的比例也同样增大 (在阈值接触到反例之 前，x=0 不变)，x 值增大
因此 ROC 曲线上的点随阈值向左移动，从左下角沿曲线向右上角移动

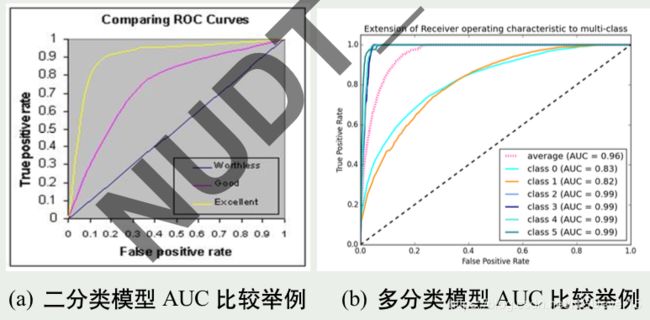
AUC for ROC 曲线

不同模型的 ROC 曲线，怎样比较优劣?类似 P-R 曲线，也看 ROC 曲 线下所包围的面积:称为 AUC(Area Under ROC Curve)
AUC 与 AP 区别:AUC 主要考察模型对正样本以及负样本的覆盖能力(即“找的全”)，而 AP 主要考察模型对正样本的覆盖能力以及识别能 力(即对正样本的“找的全”和“找的对“

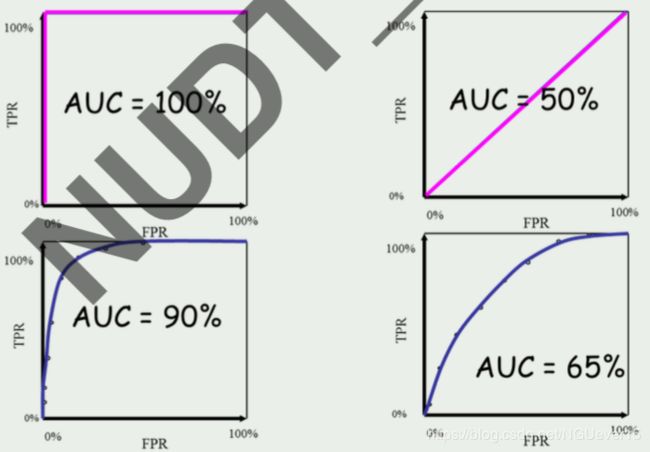
若一个学习器的 ROC 曲线被另一个学习器的曲线完全包住，则可断言 后者性能优于前者
若两条 ROC 曲线交叉，则难以一般性断言孰优孰劣。此时如果一定要 进行比较，则可以用 AUC 来进行比较

梯度优化