数学建模——计算机工具的使用(1)——SPSS操作以及在统计分析中的应用
文章目录
- 本文指南
- 一、SPSS简介
- 二、SPSS操作
- 1. 基本步骤
- 2. 数据管理(Data Management)
- 1. 主界面
- 2. 变量视图
- 1. 定义变量
- 2.数据的输入与编辑
- 3. 数据转换
- 1.根据已存在的变量建立新变量
- 2. 对观测(case)记录进行排序
- 3. 观测或变量转置
- 4. 文件合并
- 5. 选取观测子集
- 6. 其它转换
- 3. 统计分析(Statistical Analysis)
- 4. 图形分析(Graphical Analysis)
- 1. 统计图
- 2. 图形分析过程
- 3. 统计图类型及形式
- 5. 输出窗口(Output Management)
- 三、统计数据的收集、整理与描述
- 1. 统计数据的收集
- 1. 概念
- 2.收集方法
- 2. 统计数据的整理
- 1. 整理方法
- 2. 操作流程(图示)
- 3. 统计数据的描述
- 3.1 分布的中心
- 3.2 分布的形状
- 3.3 偏度与峰度
- 3.4 SPSS操作
- 四、由样本推断总体
- 1. SPSS假设检验的实现方法
- 2. 例题
- 五、方差分析
- 5.1 单因素方差分析
本文指南
- 本文讲解SPSS操作以及基础数据分析概念。
- 文章立志于打造字典级SPSS操作指南,因此建议读者根据目录适当食用。
- 本应用将持续更新到2020年2月14日美赛,主要更新内容集中在分析(高级)内容,主要采取的形式是链接到我的其他博客中。
- 文章所使用的资料来源集中于《数学建模》书籍,以确保内容的准确性,并采用图示操作形象化文字描述。当然本文内容还有大量的其他资料来源以及浅薄的个人经验整理。
- 如果你在阅读时发现了错误,请在下方评论区进行评论,万分感谢。
- 如果你觉得内容尚可,感谢点赞。
- 最后,祝愿诸位与我共同进步,学有所成。
一、SPSS简介
- 在国际学术界有条不成文的规定,即在国际学术交流中,凡是用SPSS软件完成的计算和统计分析,可以不必说明算法。
- SPSS 的基本功能包括数据管理、统计分析、图表分析、输出管理等等。
- SPSS 统计分析过程包括描述性统计、均值比较、一般线性模型、相关分析、回归分析、对数线性模型、聚类分析、数据简化、生存分析、时间序列分析、多重响应等几大类,每类中又分好几个统计过程,比如回归分析中又分线性回归分析、曲线估计、Logistic 回归、Probit 回归、加权估计、二阶段最小二乘法、非线性回归等多个统计过程,而且每个过程中又允许用户选择不同的方法及参数。
- SPSS 也有专门的绘图系统,可以根据数据绘制各种图形。
二、SPSS操作
1. 基本步骤
以统计分析为引:
- 录入数据或者打开一个已经存在的数据文件,根据需要进行数据转换;
- 选择合适的统计分析过程,选择统计分析所采用的方法和参数;
- 分析SPSS 输出的结果,并保存结果。
2. 数据管理(Data Management)
1. 主界面
- 启动SPSS 后,出现的界面是数据编辑器窗口,它的底部有两个标签:Data View(数据视图)和Variable View(变量视图),它们提供了一种类似于电子表格的方法,用以产生和编辑SPSS 数据文件。
- 与Excel的一些区别
- 列是变量,即每一列代表一个变量(Variable)或一个被观测量的特征。
- 行是观测,即每一行代表一个个体、一个观测、一个样品,在SPSS 中称为事件(Case)。
- 单元包含值,即每个单元包括一个观测中的单个变量值。单元(Cell)是观测和变量的交叉。与电子表格不同,单元只包括数据值而不能含公式。
- 数据文件是一张长方形的二维表。数据文件的范围是由观测和变量的数目决定的。可以在任一单元中输入数据。如果在定义好的数据文件边界以外键入数据,SPSS 将数据长方形延长到包括那个单元和文件边界之间的任何行和列。
- 如果要分析的数据还没有录入,可用数据编辑器来键入数据并保存为一个SPSS数据文件(其默认扩展名为sav)。

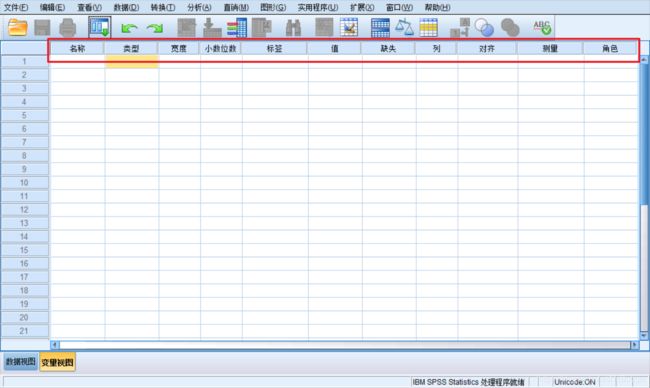
2. 变量视图
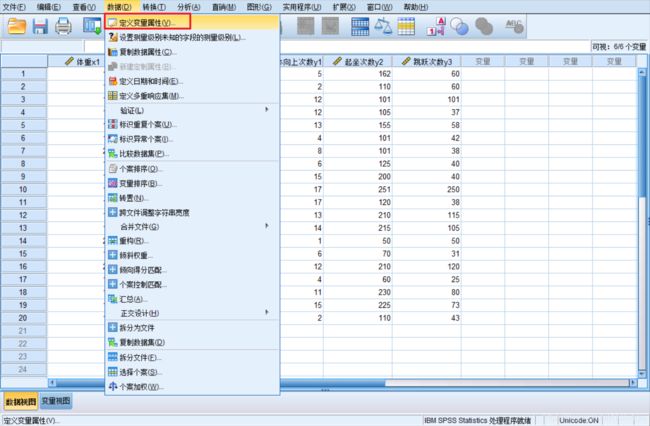
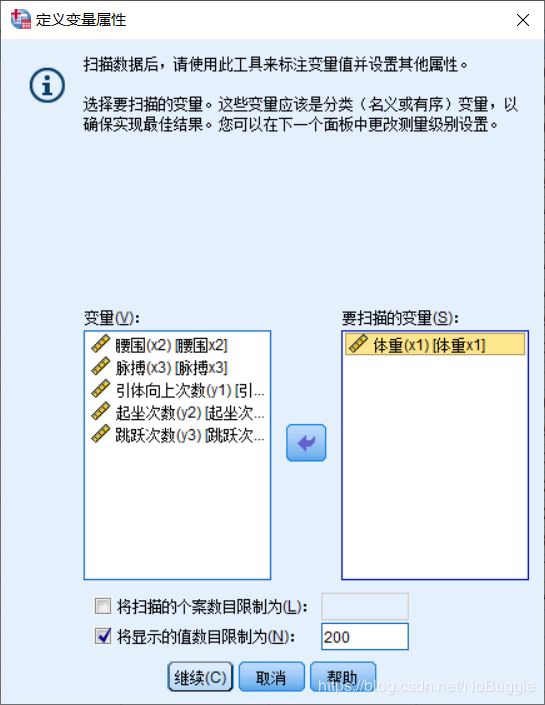
1. 定义变量
-
操作步骤
-
变量定义信息的解释
- Name:定义变量名。变量名必须以字母或字符@开头,其它字符可以是任何字母、数字或_、@、#、$等符号。变量名总长度不能超过8 个字符(即4个汉字)。
- Type:定义变量类型。SPSS 的主要变量类型有:Numeric(标准数值型)、Comma(带逗号的数值型)、Dot(圆点作小数点的数值型)、Scientific Notation(科学记数法)、Date(日期型)、Dollar(带美元符号的数值型)、Custom Currency(自定义型)、String(字符型)。单击Type相应单元中的按钮,选择合适的变量类型并单击OK。

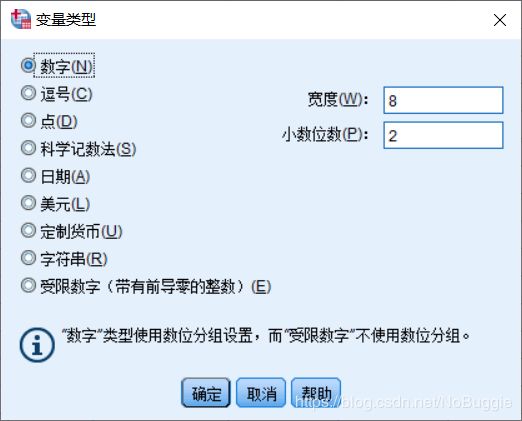
- Width:变量长度。设置数值变量的长度,当变量为日期型时无效。
- Decimal:变量小数点位数。设置数值变量的小数点位数,当变量为日期型时无效。
- Label:变量标签。变量标签是对变量名的进一步描述,变量只能由不超过8 个字符组成,8 个字符经常不足以表示变量的含义。而变量标签可长达120 个字符,变量标签对大小写敏感,显示时与输入值完全一样,需要时可用变量标签对变量名的含义加以解释。
- Value:变量值标签。值标签是对变量的每一个可能取值的进一步描述。
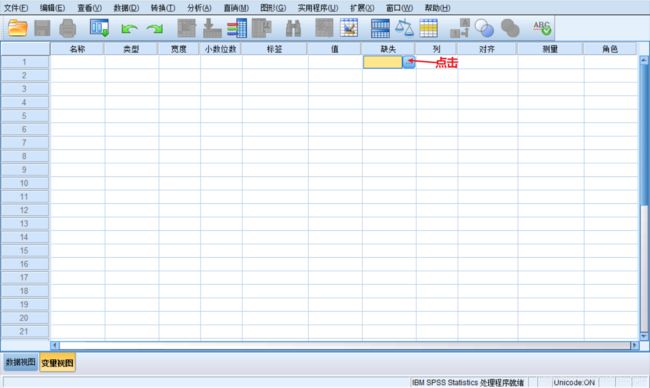
- Missing:缺失值的定义方式。
SPSS 有两类缺失值:系统缺失值和用户缺失值。 - Column:变量的显示宽度。输入变量的显示宽度,默认为8。
- Align:变量显示的对齐方式。 选择变量值显示时的对齐方式:Left(左对齐)、Right(右对齐)、Center(居中对齐)。
- Scale:变量的测量尺度。根据变量测量精度不同,可把变量由低到高分为四种尺度:定类变量、定序变量、定距变量和定比变量。
- 定类变量。定类变量由称为名义(nominal)变量。这是一种测量精度最低、最粗略的基于“质”因素的变量,它的取值只代表观测对象的不同类别,例如“性别”变量、“职业”变量等都是定类变量。定类变量的取值称为定类数据或名义数据。定类数据的共同特点是用不多的名称来加以表达,并由被研究变量每一组出现的次数及其总计数所组成,这种数据是枚举性的,即由计数一一而得。唯一适合于定类数据的数学关系是“等价关系”。因而,在定类数据中,同一组内各单位是等价的,同时若更换各不同组的符号并不会改变数据原有的基本信息。因此,最常用来综合定类数据的统计量是频数、比率或百分比等。

- 定序变量。定序变量由称为有序(ordinal)变量、顺序变量,它的取值大小能够表示观测对象的某种顺序关系(等级、方位或大小等),也是基于“质”因素的变量。例如:“最高学历”变量的取值是:1-小学及以下、2-初中、3-高中、中专、技校、4-大学专科、5-大学本科、6-研究生以上。由小到大的取值能够代表学历由低到高。定序变量的取值称为定序数据或有序数据。适合于定序数据的数学关系是“大于(>)”和“小于(<)”关系。在定序数据中,同一组内各单位是等价的,相邻组之间的单位是不等价的,它们存在“大于”或“小于”的关系。而且进行保序变换(或称单调变换),不改变数据原有的基本信息即等级顺序。最适合用于综合定序数据取值的集中趋势的统计量是中位数。

- 定距变量。定距变量又称为间隔(interval)变量,它的取值之间可以比较大小,可以用加减法计算出差异的大小。例如,“年龄”变量,其取值60与20相比,表示60岁比20岁大,并且可以计算出大40 岁(60-20)。定距变量的取值称为定距数据或间隔数据。定距数据是一些真实的数值,具有公共的、不变的测定单位,可以进行加减乘除运算。定距数据的基本特点是两个相同间隔的数值的差异相等。对于定距数据,不仅可以规定“等价关系”以及“大于关系”和“小于关系”,而且也可以规定任意两个相同间隔的比值或差值。如果将每个数值分别乘以一个正的常数再加上一个常数,即进行正线性变换,并不影响定距数据原有的基本信息。因此,常用的统计量如均值、标准差、相关系数等都可直接用于定距数据。
- 定比变量。定比变量又称为比率(ratio)变量,它与定距变量意义相近,细微差别在于定距变量中的“0”值只表示某一取值,不表示“没有”。例如,人的身高就是一个定比变量,如果身高值为“0”米,则表示这个人不存在。定比变量的“0”值表示“没有”。而在测定温度的摄氏表中,0oC 并不表示没有温度,因为还有在零度以下的温度。定比变量的取值称为定比数据或比率数据。定比数据也同样可进行算术运算和线性变换等。通常对定距变量和定比变量不需要加以区别,两者统称为定距变量或间隔变量。
- 一般地,定类变量(名义变量)和定序变量(有序标量)用于描述定性数据,属于定性变量;而定距变量和定比变量用于描述定量数据,属于定量变量。
- 定类变量。定类变量由称为名义(nominal)变量。这是一种测量精度最低、最粗略的基于“质”因素的变量,它的取值只代表观测对象的不同类别,例如“性别”变量、“职业”变量等都是定类变量。定类变量的取值称为定类数据或名义数据。定类数据的共同特点是用不多的名称来加以表达,并由被研究变量每一组出现的次数及其总计数所组成,这种数据是枚举性的,即由计数一一而得。唯一适合于定类数据的数学关系是“等价关系”。因而,在定类数据中,同一组内各单位是等价的,同时若更换各不同组的符号并不会改变数据原有的基本信息。因此,最常用来综合定类数据的统计量是频数、比率或百分比等。
2.数据的输入与编辑
health.xlsx
3. 数据转换
在理想情况下,输入的原始数据完全适合要执行的统计分析模型,遗憾的是,这种情况很罕见,经常需要通过数据转换来提示变量之间的真实关系。利用SPSS 可进行从简单到复杂的数据转换。
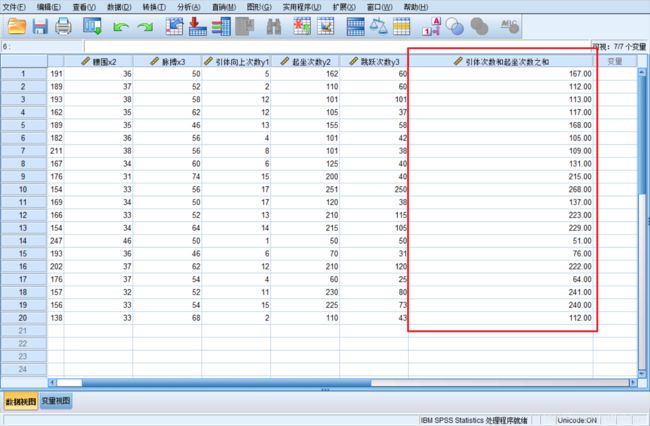
1.根据已存在的变量建立新变量
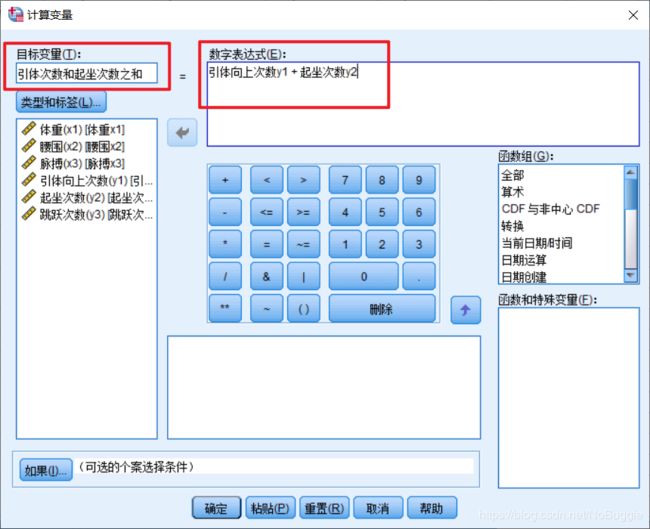
转换(Transform)==》计算变量(Compute Variable)
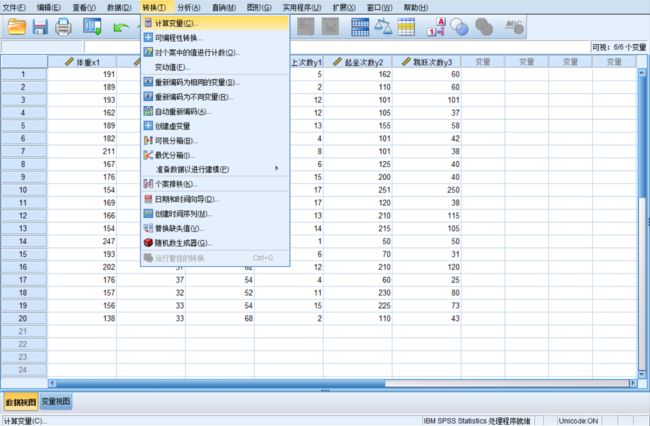

操作指引:
-
在对话框中的Target Variable(目标变量)下框中输入符合变量命名规则的变量名,目标变量可以是现存变量或新变量。
-
对话框中Numeric Expression(数值表达式)下的文本
框用于输入计算目标变量值的表达式。表达式能够使用左下框列出的现存变量名、计算器板列出的算术运算符和常数和Functions(函数)列表框显示的各种函数等。可以在文本框中直接输入和编辑表达式,也可以使用变量列表、计算器板和函数列表将元素粘贴到文本框中。 -
计算器板下面有一个IF按钮,单击该按钮打开条件表达式对话框。在条件表达式对话框中指定一个逻辑表达式,一个逻辑表达式对每一个观测(case)返回真、假或缺失值。如果一个逻辑表达式的结果是真,就把转换应用于那个观测;如果结果是假或缺失值,就不对那个观测应用转换。
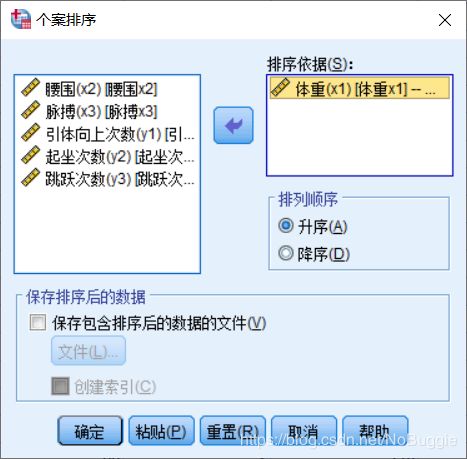
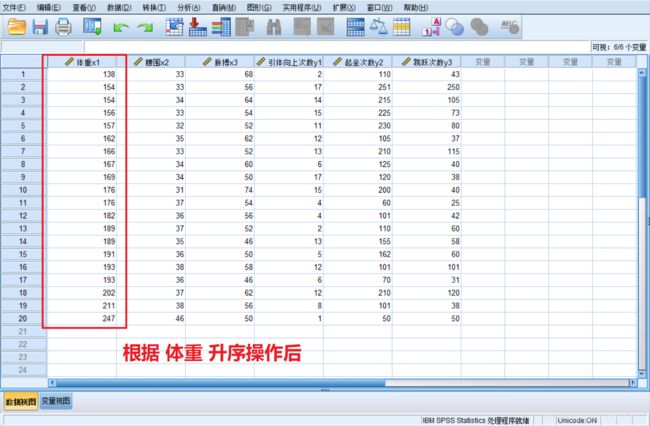
2. 对观测(case)记录进行排序
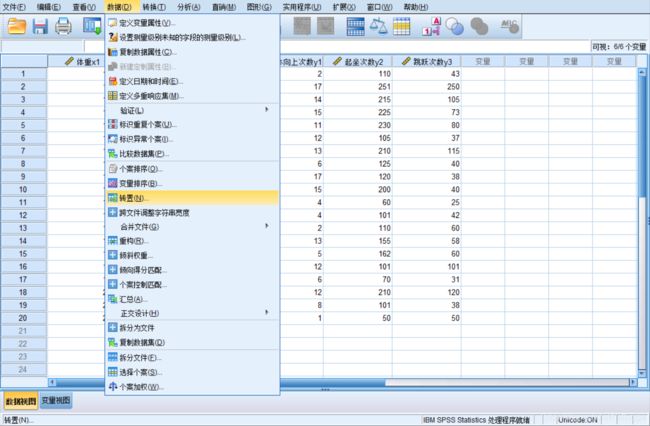
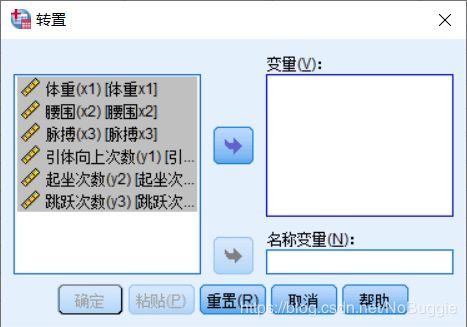
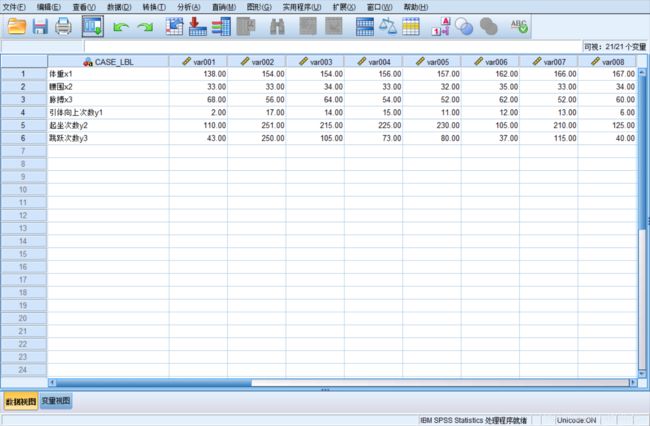
3. 观测或变量转置
4. 文件合并
- 作用:可以将两个或更多个数据文件合并在一起,即可将具有相同变量但观测不同的文件合并,也可将观测相同变量不同的文件相合并。
- 操作指引:
- 选择Data=>Merge Files=>Add cases从第二个文件即外部SPSS数据文件相当前工作数据文件追加观测。
- 选择Data=>MergeFiles=>Add Variables 合并含有相同观测但不同变量的两个SPSS 外部文件。
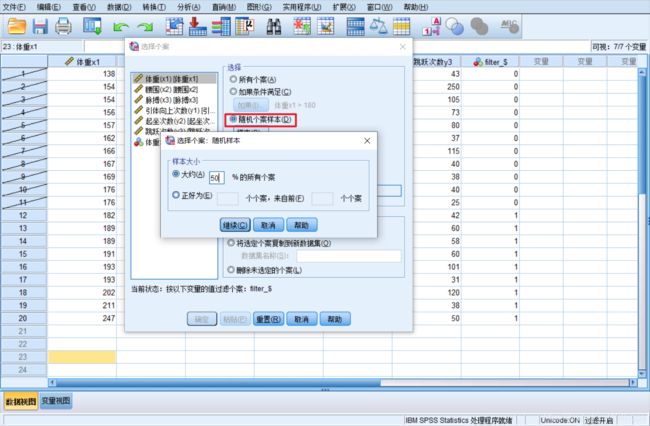
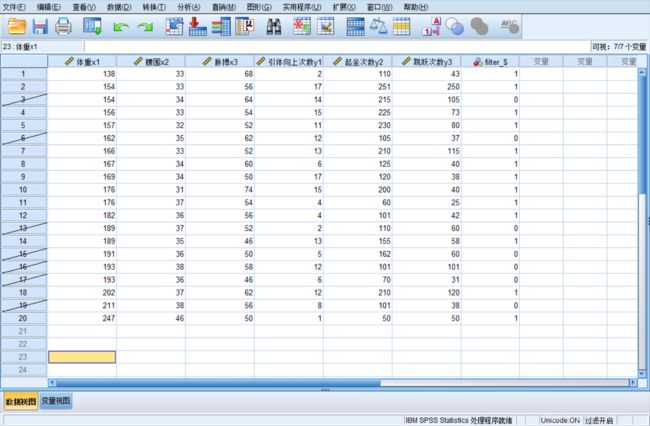
5. 选取观测子集
-
作用:可以同时对不同的观测子集做不同的统计分析。
-
操作指引: 可以选择Data=>Select Cases 根据包含变量和复杂的表达式的准则把统计分析限于某一特定观测子集,也可选取一个随机观测样本。

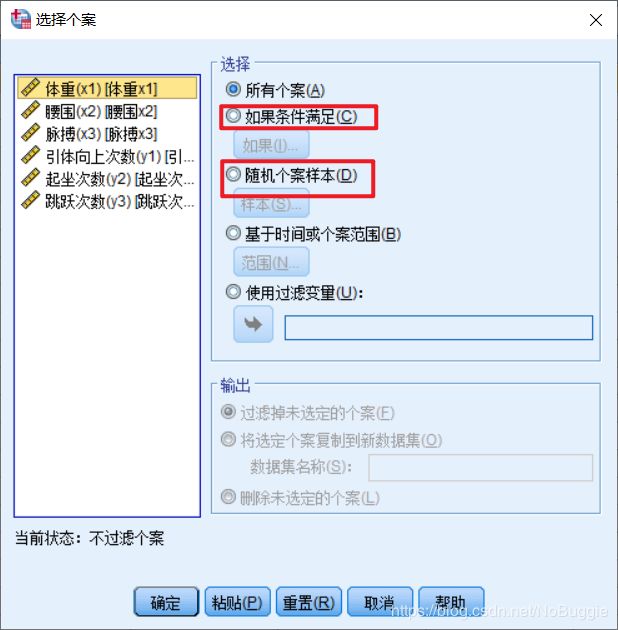
-
示例图示操作:
6. 其它转换
- 数据汇总,Data=>Aggregate;
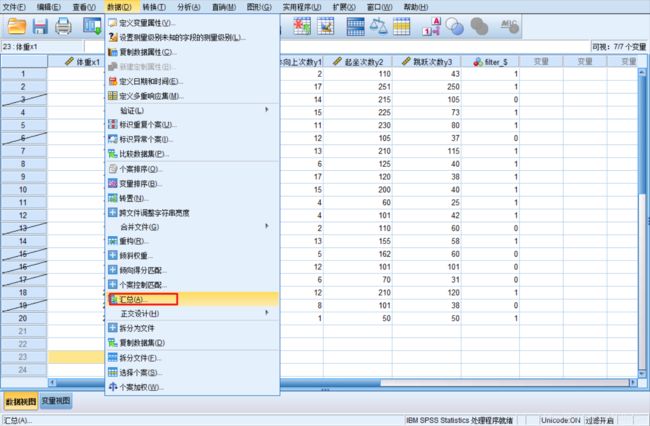

- 数据加权,Data=>Weight Cases;
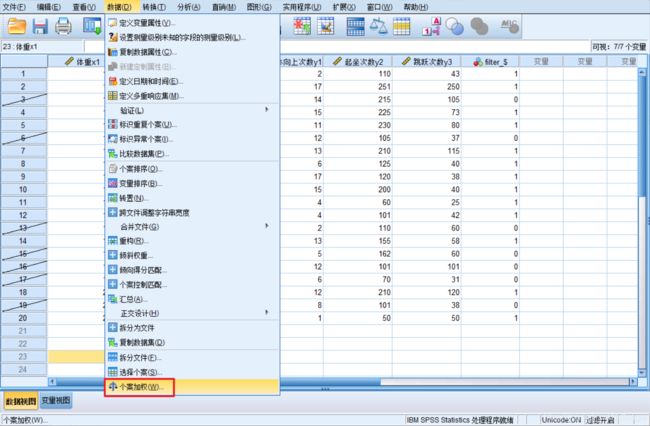
- 数值编码,Transform=>Recode;

- 数据求秩,Transform=>Rank Cases;
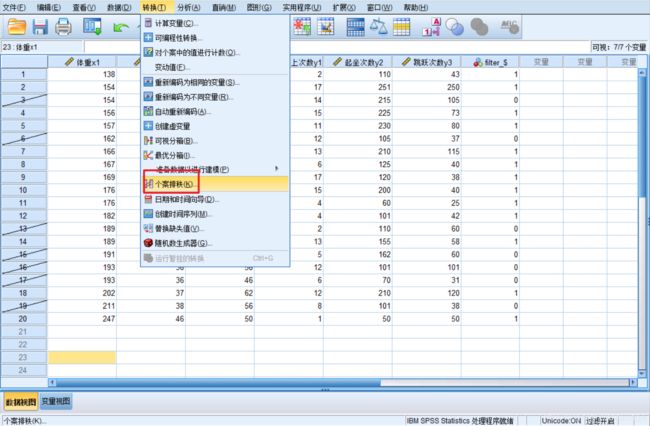
- 产生时间序列,Tranform=>Create Time Series。
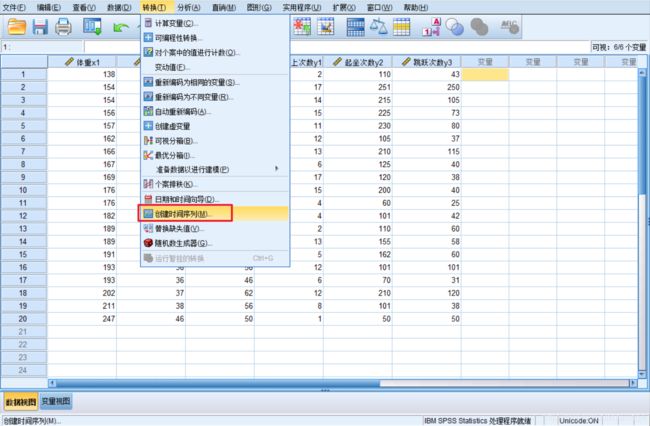
3. 统计分析(Statistical Analysis)
在SPSS 中建立了数据文件或打开一个数据文件之后,选择正确的统计分析方法,是得到正确分析结果的关键步骤。统计分析过程在主菜单Analyze(分析)中的下拉菜单中。
- 典型相关分析
- 待补充中
4. 图形分析(Graphical Analysis)
1. 统计图
- 概念:统计图是用点的位置、线段的升降、直条的长短或面积的大小等方法来表达统计数据的一种形式,它可以把资料所反映的变化趋势、数量多少、分布状态和相互关系等形象直观地表现出来,以便于读者的阅读、比较和分析。
- 特点:统计图具有简明生动、形象具体和通俗易懂的特点。
- 来源:SPSS 的图形分析功能很强,许多高精度的统计图形可从Analyze菜单的各种统计分析过程产生,也可以直接从Graph 菜单中所包含的各个选项完成。
2. 图形分析过程
- 建立或打开数据文件,若数据文件结果不符合分析需要,则必须转换数据文件结果;
- 生成图形;
- 修饰生成的图形,保存结果。
3. 统计图类型及形式
- 常用类型:条形图、线图、面积图、圆饼图、散点图、直方图、箱线图等等。
- 两种形式:一种为一般图形,另一种为交互式图形,交互式图形提供了更多的选项,可绘制出更强大
的图形。
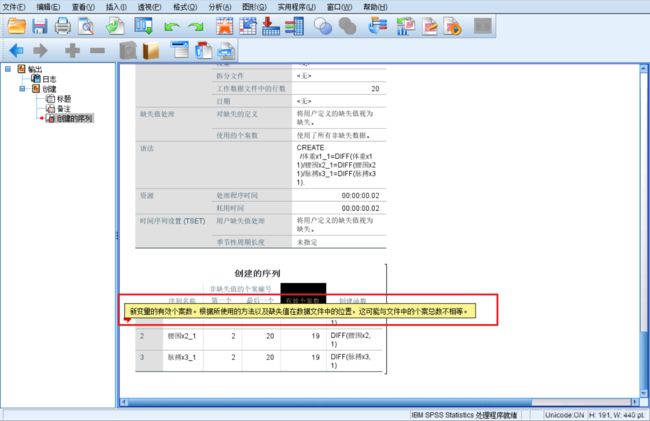
5. 输出窗口(Output Management)
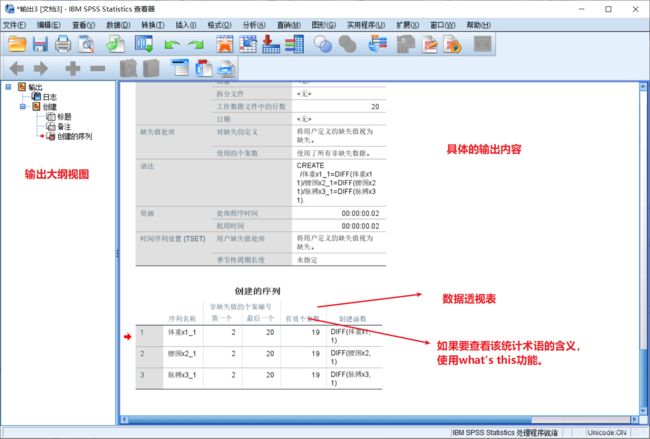
What‘s This?:双击该数据透视表,右击术语,在弹出的快捷菜单中选择What’s This,就可获得该术语的简单定义。

三、统计数据的收集、整理与描述
1. 统计数据的收集
1. 概念
统计数据的收集就是统计调查,它按研究的目的和要求,有组织地向调查对象收集相关的各种资料。为了保证统计数据资料的完整性、准确性和及时性,必须熟悉各种收集方法及各自的特点。
2.收集方法
- 问卷调查
问卷是调查者向被调查者了解情况或征询意见时所运用的同一设计的调查表。绝大多数旨在收集定量数据的调查都要采用某种形式的问卷,才会使调查得以顺利完成,并获得令人满意的数据。 - 普查法
普查,是按照一定标准时间对普查对象的全部单位无一例外地逐个进行的调查。普查按门类划分,可分为人口普查、工业普查、商业普查、农业普查、第三产业普查等。普查按区域划分,有宏观、中观和微观之分。一般而言,我们经常提起的普查为宏观普查。 - 抽样调查
普查的覆盖面宽,但其耗费的人力、物力、财力太大,在统计调查中抽样调查更为常用。抽样调查是从调查对象的总体中,按照一定的抽样原则抽取一部分单位作为样本,并以对样本进行调查的结果来推断总体的方法。
根据抽样方法是否随机,可将抽样调查分为随机抽样和非随机抽样两大类。 - 典型调查
典型调查是从调查对象的总体中选取一个或几个有代表性的单位进行全面、深入的调查。调查单位可依不同调查目的选取企业、学校、个人、家庭等。
典型调查的目的就是通过对某个典型的深入分析来概括和反映全面。因此,典型调查要求典型对总体推断有一定的代表性,这也是典型调查的关键。典型的代表性可以从动态、静态两个方面来衡量。从动态上来讲,是指事物的发展趋势;从静态上来讲,是指事物的共同属性与差异。 - 观察法
观察法是观察者深入现场或进入一定环境,观察调查对象,获取第一手资料的方法。调查人员直接到调查现场,耳闻目睹顾客对市场的反映和公开言行,或者利用照相机、监视器等现代化器械间接地进行观察来收集资料等,都属于观察法。
观察法的特点就是从侧面观察被观察者的言行和反映,一般不直接向被调查人提出问题,所以,被调查者往往是在不知情的状况下被调查的。 - 实验法
实验法是研究者根据一定的研究目的,控制某种市场条件,或在人工环境中使一定的现象产生,通过观察、记录收集资料,以揭示其发生原因或规律的方法,是一种复杂、高级调查方法。 - 集体访谈法
集体访谈法是访问调查法的延伸和扩展,是调查者邀请若干被调查者,通过集体访谈的方式了解有关情况或研究实用统计学有关问题的方法。
2. 统计数据的整理
收集统计数据之后,要对获取的数据进行系统化、条理化地整理,以提取有用的信息。
1. 整理方法
- 统计分组
根据统计研究的目的和客观现象的内在特点,按某个标志(或几个标志)把被研究的总体划分为若干个不同性质的组,称为统计分组。统计分组的对象是总体。从分组的性质来看,分组具有分和双重含义。 - 频数分布与频率分布
- 将数据按其分组标志进行分组的过程,就是频数分布和频率分布形成的过程。表示各组的次数称为频数,各组次数与总次数之比称为频率。 频数分布就是观察值按其分组标志分配在各组内的次数,由分组标志序列和各组相对应的分布次数两个要素构成。由分组标志序列和各组相应的频率构成频率分布。
- 在平面直角坐标系上,将分组标志作为横轴并将各组频数(频率)作为纵轴,给出各组的长方形图即直方图。与直方图相似作用的图示是折线图,它以各组标志值中点位置作为该组标志的代表值,然后用折线将各组频数连接起来。
- 当所观察的次数很多,组距很小并且组数很多时,所绘出的折线图就会越来越光滑,逐渐形成一条光滑的曲线,这种曲线即频数分布曲线,反映了数据的分布规律。统计曲线在统计学中很重要,是描绘各种分布规律的有效方法。常见的频数分布曲线有正态分布曲线、偏态分布曲线、J 型分布曲线和 U 型分布曲线。
- 累计频数分布与频数分布
为了统计分析的需要,有时为了观察某一数值以上或某一数值以下频数或频率之和,这就需要在基本分组的基础上绘出累计频数或累计频率。由表的上方向表的下方的频数或频率相加就称为“向下累计”,反之称为“向上累计”。
累计频率(或频率)分布曲线,可用以研究财富、土地和工资收入的分配是否公平。这种累计分布曲线图最早由美国洛伦茨博士(Dr. M. O. Lorenz)提出的,故又称洛伦茨曲线图。
2. 操作流程(图示)
在SPSS 中进行频数(率)分析的步骤为:
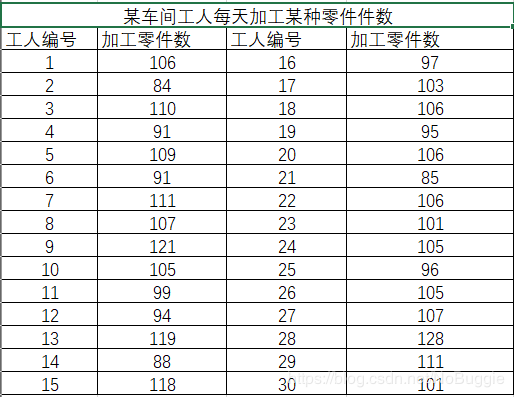
- 导入Excel文件
文件:某车间工人每天加工某种零件件数
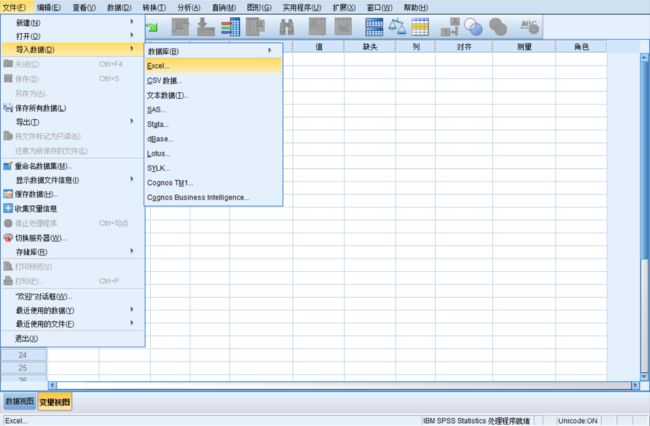

选择对应的excel文件,点击打开。
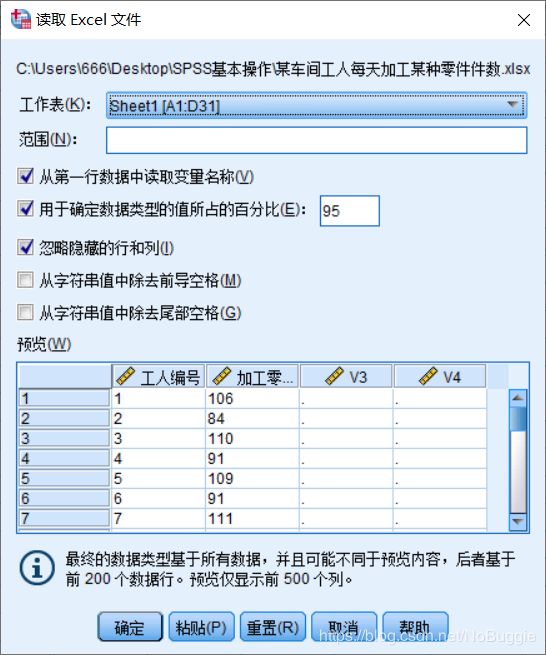
点击确定,我们可以得到如下界面。

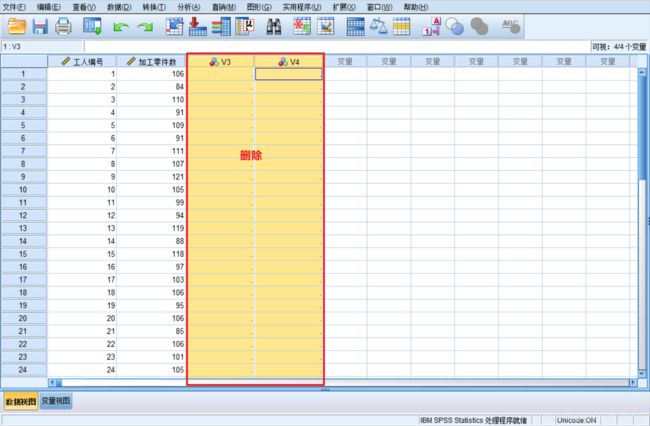
- 处理数据视图
我们只需保留前两个有效的变量,因此删除V3、V4。


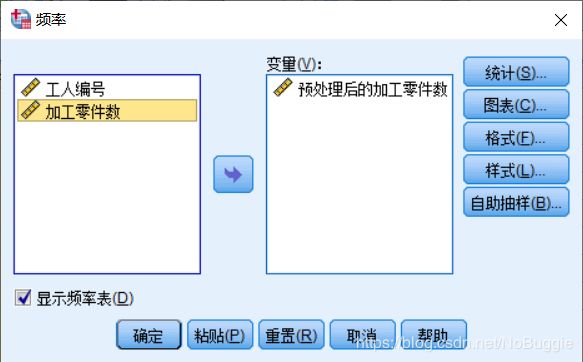
- 选择Analyze(分析)=>Descriptive Statistics(描述统计)=>Frequencies(频率)…,弹出Frequencies(频率)主对话框。现欲对 加工零件数 进行频数分析,在对话框左侧的变量列表中选加工零件数,单击按钮使之进入Variable(s)(变量)列表框,并选择Display FrequencyTables 显示频率表。

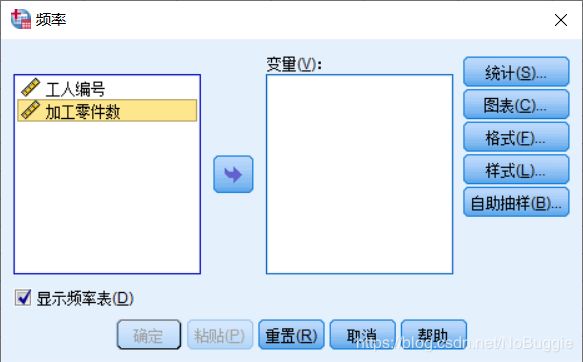

- 可单击Format…按钮弹出Frequencies:Format(格式) 子对话框,在Order by栏中有四个选项:
Ascending values(按值的升序排序) 为根据数值大小按升序从小到大作频数分布;
Descending values(按值的降序排序) 为根据数值大小按降序从大到小作频数分布;
Ascending counts(按计数的升序排序) 为根据频数多少按升序从少到多作频数分布;
Descending counts(按计数的降序排序) 为根据频数多少按降序从多到少作频数分布。
这里选Ascending values(按计数的升序排序)项后点Continue钮返回Frequencies 主对话框。

- 可单击Statistics(统计)…按钮,弹出Frequencies(频率):Statistics(统计)子对话框,并单击相应项目,在作频数表分析的基础上,附带作各种统计指标的描述,特别是可进行任何水平的百分位数计算。
这里不选。

- 可单击Charts(图表)…钮,弹出Frequencies:Charts 子对话框,用户可选三种图形:直条图(Bar Charts)、饼图(Pie Charts)和直方图(Histogram)。这里选择Histogram项,并选择With Normal Curve 要求绘制正态曲线。单击Continue 按钮返回Frequencies主对话框,再单击OK 钮即可得到(累计)频数(频率)分布表和直方图。
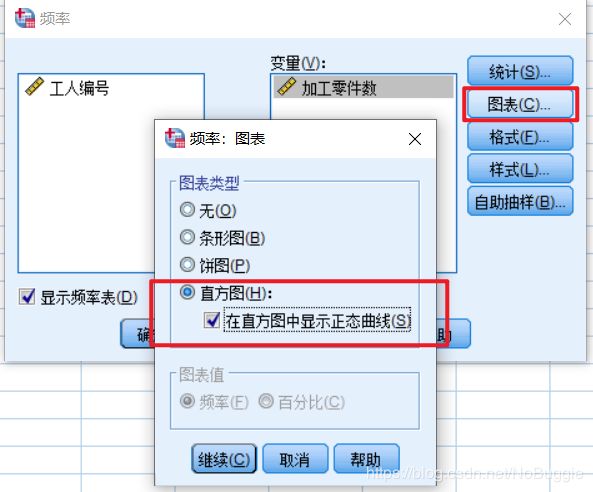
- 不出意外的话,你应该会在输出窗口中看到如下输出结果。


- 应该注意的是,SPSS 在未特别指定的情形下,直方图或频数分布表是按照原始数值逐一作频数分布的,这与日常需要的等距分组、且组数保持在一定数目的要求不符。

- 预处理。
在调用Frequencies 统计过程命令之前,可先对原始数据进行预处理:已知最小值为84,最大值为128 , 故可要求分成5组,起点为80,组距为10。
操作流程:-
选择Transform(转换)=>Recode Into Different Variable(重新编码为不同变量)…;

-
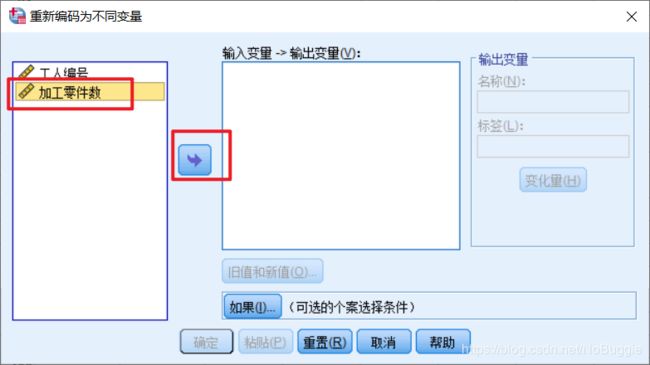
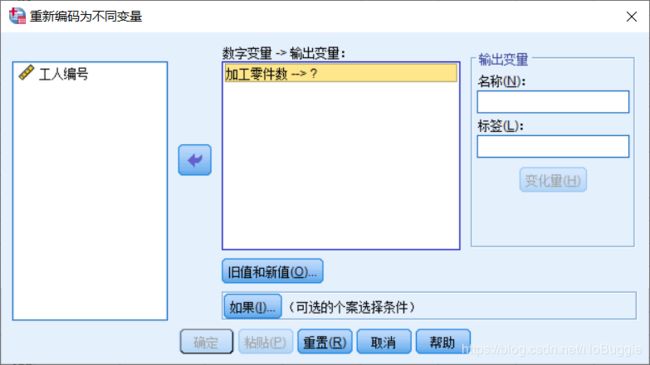
在弹出的Recode Into DifferentVariable(重新编码为不同变量) 对话框中选定加工零件数,单击按钮使之进入Numeric Variable → Output Variable(数字变量→输出变量)列表框;
-
在Output Variable(输出变量)栏的Name(名称) 文本框中输入预处理后的加工零件数,单击Change (变化量)按钮表示生成新生成的变量名为 预处理后的加工零件数。


-
单击Old and New Values(旧值和新值)按钮弹出Record Into Different Variable(重新编码为不同变量):Old and New Values(旧值和新值) 子对话框;
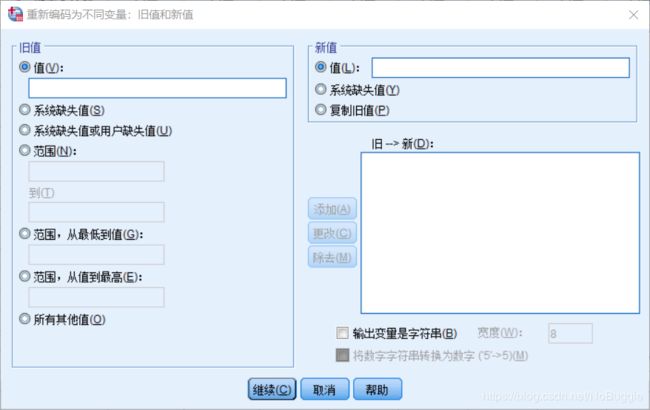
-
在Old Value(旧值)选项中单击Range(范围)项,输入第一个分组的数值范围:80~89,在New Value(新值)栏内输入新值:80,单击Add(添加)按钮,依此将各组的范围及对应的新值逐一输入,最后单击Continue 按钮返回,再单击OK 按钮即完成。
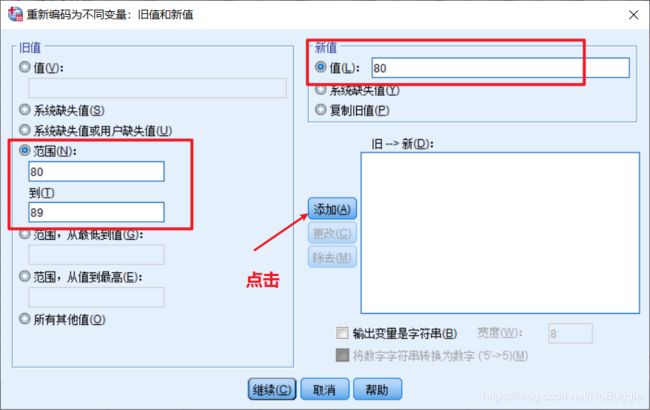
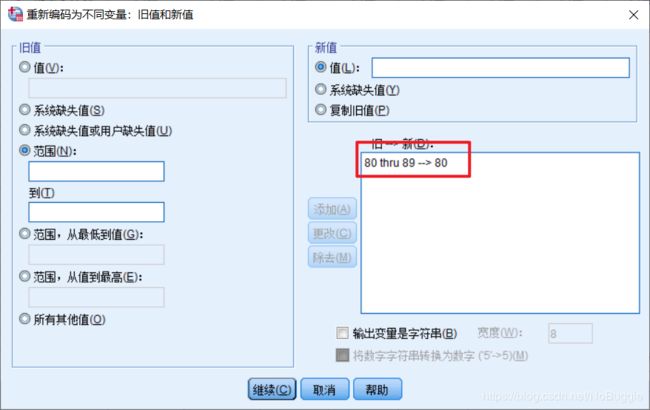

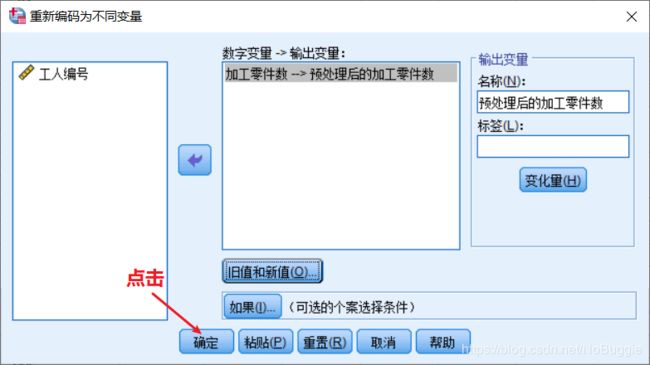
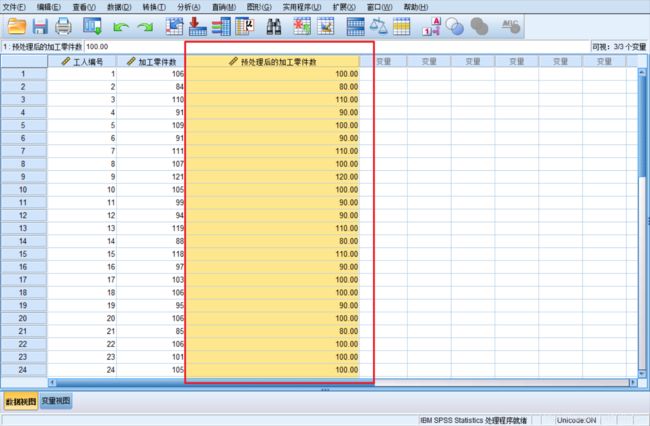
-
系统在原数据库中生成一新变量为 预处理后的加工零件数,这时再调用Frequencies 统计过程将输出等距分组且组数为5 的频数分布表。
-
3. 统计数据的描述
将数据整理成频率(频数)分布后,数据的数量规律性就可以大致地呈现在分布的类型和特点上。但频数分布给予我们的是一个大致的分布形状,还缺少代表性的数量特征值精确地描述出不同的统计数据分布。作为统计数据的代表值,一个是分布的中心,反映分布的集中趋势,另一个是分布的形状,反映分布的离散程序。
3.1 分布的中心
定义分布的中心有许多不同的方式。这里介绍三种最常用的,即众数、中位数和平均数。
- 众数(mode)
一个分布的众数定义为频数出现最多的变量值。在正态分布和一般的偏态分布中,分布曲线最高点所对应的数值即是众数。如果没有明显的最高点,众数可以不存在。当然,如果有两个最高点,也可以有两个众数。众数很容易求得,一般只要看一眼即可。它特别使用于描述定类变量和定序变量的数据。定距变量的数据分组后也可近似地用某个组的组中值来表示众数的大小。但众数并不是一个描述中心的很好的代表值,它常常依赖于数据的分组情况,即分组数改变的话众数可能就会有较大的变化。而且众数也可能不唯一。 - 中位数(median)与分位数
中位数是数据排序后,位置在最中间的数值。显然,中位数将数据分成两半,一半数据比中位数大,一半数据比中位数小。用中位数来代表总体标志值的一般水平,可以避免代表值受数列中极端值的影响,稳定性比较好,有时更有代表性。 - 平均值(均值)(mean)
平均数是数据集中趋势的最主要测度值。
3.2 分布的形状
只从均值来看待数据是片面的,我们还必须考虑数据的分布形状。用于描述数据分布形状,即分布关于其中心的波动程度的代表值有:极差、内距、方差和标准差等,它们描述了分布的离散程度和差异程度。
- 极差(range)
极差也称为全距,是最大值与最小值之间的距离,它是数据离散或差异程度的最简单测度值。 - 内距(Inter-Quartile Range,IQR)
内距又称为四分位差,是两个四分位数之差,即内距IQR = 高四分位数 - 低四分位数。与极差类似,内距也是由两个值之差决定的,也是不全面的。但由于这两个值之差代表了中间50%部分的长度,所以比极差能更好地描述分布的特征。
例如,若内距比较小,则说明数据比较集中在中位数附近;反之则比较分散。内距常和中位数一起用来描述一个定距特别是定序测量数据的分布。 - 方差(variance)和标准差(standard deviation)
3.3 偏度与峰度
前面讨论了分布的集中趋势和离散趋势。要全面了解分布的特点,仅了解分布的集中趋势和离散程度是不够的,还需要了解分布是否对称和集中趋势高低等特征。偏度和峰度就是对分布的进一步描述。
- 偏度
所谓偏度是指反映频数分布偏态方向和程度的测度。从方向上看,偏度分左偏和右偏两种。 - 峰度
所谓峰度,是指频数分布曲线高峰的形态,即反映分布曲线的尖峭程度的测度。在频数分布中,有的频数分布曲线与正态曲线相比是尖顶,有的则是平顶,峰度就是用来衡量频数分布曲线的高耸程度的一个数字特征。当峰度大于3时,表示分布曲线的高峰是尖顶高峰;当峰度小于3时,表示分布曲线的高峰是平顶高峰。
3.4 SPSS操作
- 导入数据
文件:某车间工人每天加工某种零件件数

- Analyze(分析)=>Descriptives Statistics(描述性统计)=>Descriptives(描述)…, 打开Descriptives(描述)主对话框。在主对话框左边列表中选定变量加工零件数,单击按钮使之进入Variable(s)(变量)列表框。

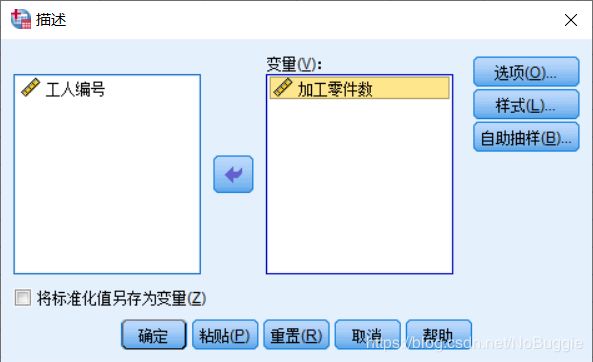
- 单击Options(选项)…按钮,打开Descriptives(描述):Options (选项)子对话框。选择均值(Mean)、总和(Sum)、标准差(Std. Deviation)、方差(Variance)、极差(Range)、最小值(Minimum)、最大值(Maximum)、偏度(Skewness)和峰度(Kurtosis),选好后单击Continue按钮返回Descriptives(描述)主对话框,再单击OK按钮即可得到各种统计量的计算结果。
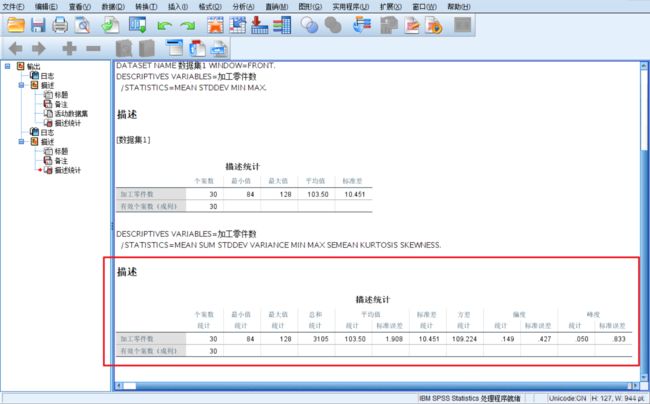
四、由样本推断总体
统计推断(Statistical inference)就是根据样本的实际数据,对总体的数量特征作出具有一定可靠程度的估计和判断。统计推断的基本内容有参数估计和假设检验两方面。概括地说,(参数估计)研究一个随机变量,推断它具有什么样的数量特征,按什么样的模式来变动,这属于估计理论的内容,而**(假设检验)推断这些随机变量的数量特征和变动模式是否符合我们事先所作的假设**,这属于检验理论的内容。
1. SPSS假设检验的实现方法
SPSS 提供了计算指定变量的综合描述统计量的过程和对均值进行比较检验的过程。
- 用于计算变量的综合统计量的Means过程
Analyze(分析)=>Compare Means(比较平均值)=>Means(平均值)
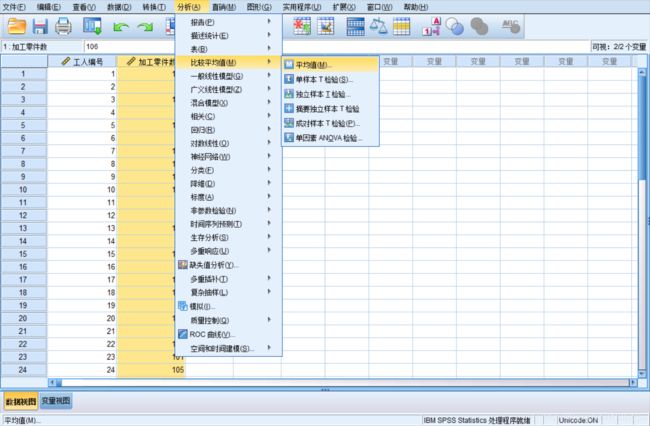
- 用于单样本的 t 检验过程
Analyze=>Compare Means=>One-Sample T Test(单样本T检验)
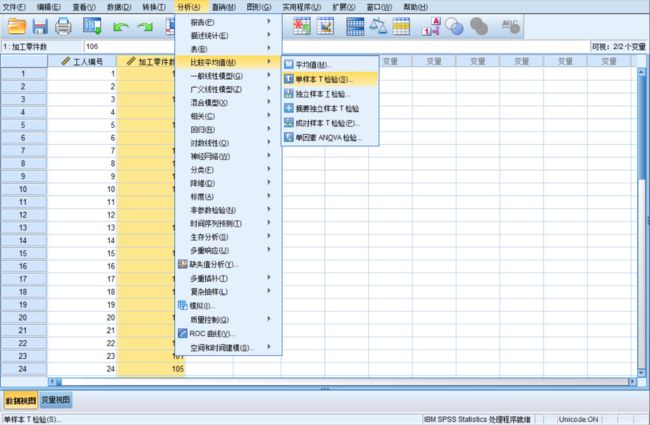
- 用于独立样本的 t 检验过程
Analyze=>Compare Means=>Independent-Sample T Test(独立样本T检验)
用于检验是否两个不相关的样本来自具有相同均值的总体。

- 用于配对样本的 t 检验过程
Analyze=>Compare Means=>Paired-Sample T Test(配对样本t检验)
用于检验两个相关的样本是否来自具有相同均值的总体。
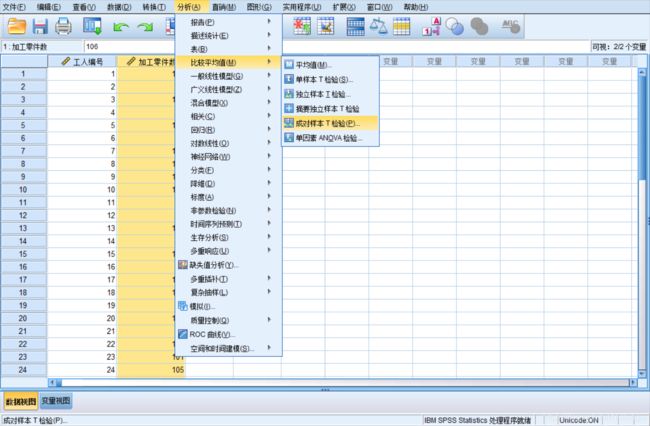
2. 例题
分别测得14 例老年性慢性支气管炎病人及11例健康人的尿中17酮类固醇排出量(mg/dl)如下,试比较两组均值有无显著性差别(α = 0.05)。

操作指引:
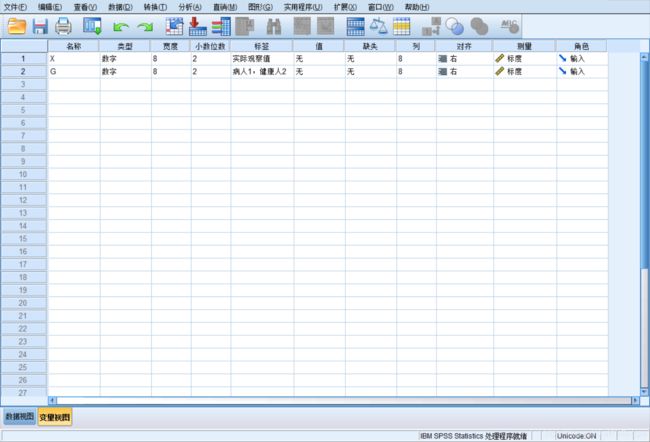
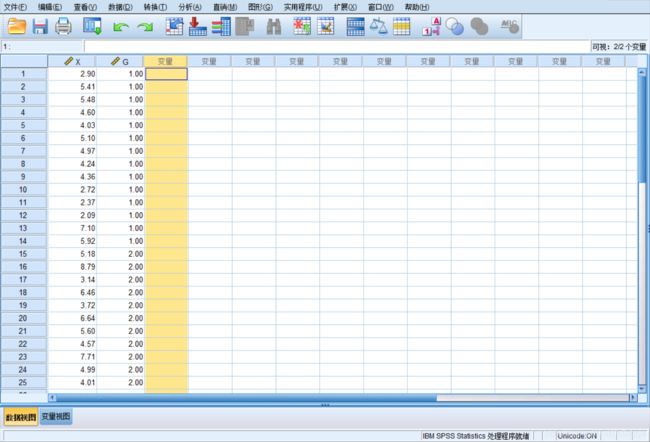
- 定义变量:把实际观察值定义为X,再定义一个变量G 来区分病人和健康人。输入原始数据,在变量G 中,病人输入1,健康人输入2。
- 选择Analyze=>Compare Means=>Independent-Samples T Test , 打开Independent-Samples T Test 主对话框。


- 从主对话框左侧的变量列表中选X,单击按钮使之进入Test Variable(s)(检验变量)列表框,选G 单击按钮使之进入Grouping Variable (分组变量)框。
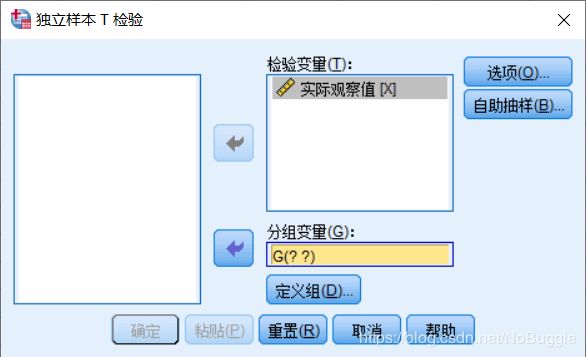
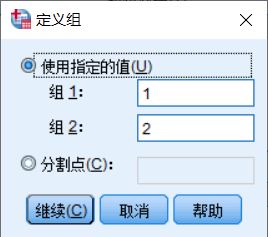
- 单击Define Groups(定义组) 按钮弹出Define Groups 定义框,在Group 1 中输入1,在Group 2中输入2,单击Continue 按钮,返回Independent-Samples T Test 主对话框,单击OK按钮即完成。
- 在输出窗口生成的内容
- 检验结果如下,经 Levene 方差齐性检验:F = 0.440, p 值= 0.514, p >α ,两总体方差无显著性差异。
- 第三行表示方差齐性情况下的t 检验的结果,第四行表示方差不齐情况下的t 检验的结果。依次显示t 值(t-value)、自由度(df)、双侧检验p 值(Sig 2-Tail)等。
- 因本例属方差齐性,故采用第三行(即Equal variances assumed)结果:t = −1.807, p = 0.084 < 0.1,差异显著,即老年性慢性支气管炎病人的尿中17 酮类固醇排出量低于健康人。
五、方差分析
5.1 单因素方差分析
方差分析是检验两个总体或多个总体的均值间差异是否具有统计意义的一种方法。方差分析与回归分析之间存在一定的关系。对于方差分析,所有的自变量都被视为定类变量;而回归分析中,自变量可以是各种测度的变量(包括定类变量、定序变量、定距变量和定比变量)。事实上,经常把方差分析看作回归分析的一种特例,几乎所有方差分析模型可以由回归模型来表示,可以用回归分析的一般方法估计出相应的参数并进行推断。