算法导论题解(二) 算法基础

1. 插入排序练习

1-1. 以图2-2为模型，说明INSERTION-SORT在数组A=<31, 41, 59, 26, 41, 58>上的执行过程。

1-2. 重写INSERTION-SORT,使之按非升序(降序)排序。

# 伪代码
INSERTION-SORT(A)
    for j = 2 to A.length
        key = A[j]
        i = j - 1
        while i >= 0 and A[i] < key
            A[i + 1] = A[i]
            i = i - 1
        A[i + 1] = key
# python代码实现: 
def insertion_sort(A):
    """插入排序-降序"""
    length = len(A)
    print("源数组: ", A)
    for j in range(1, length):
        key = A[j]
        i = j - 1
        while i >= 0 and A[i] < key:
            # 交换元素值
            A[i + 1], A[i] = A[i], A[i + 1]
            i = i - 1
        A[i + 1] = key
        print("第%d次插入排序: %s" %(j, A))
    return A


if __name__ == "__main__":
    A = [31, 41, 59, 26, 41, 58]
    sort_A = insertion_sort(A)
    print("数组降序排序结果: ", sort_A)

执行效果如下:
1-3. 考虑以下查找问题:
输入: n个数的一个序列A=和一个值v.
输出: 下标i使得v=A[i]或者当v不在A中出现时，v为特殊值NULL。
写出线性查找的伪代码，它扫描整个序列来查找v。使用一个循环不变式来证明你的算法是正确的。确保你的循环不变式满足单个必要的性质。

• 伪代码

LINEAR-SEARCH(A, value)
    for index = 1 to A.length
       if A[index] == value
            return index
    return NIL

• Python代码

def linear_search(A, value):
    """
    线性查找， 若存在，返回索引值，不存在返回空
    """
    length = len(A)
    for index in range(length):
        if A[index] == value:
            return  index
if __name__ == '__main__':
    A = [31, 41, 59, 26, 41, 58]
    find_key = 26
    print("正在在序列%s中寻找关键字%s" %(A, find_key))
    key_index = linear_search(A, find_key)
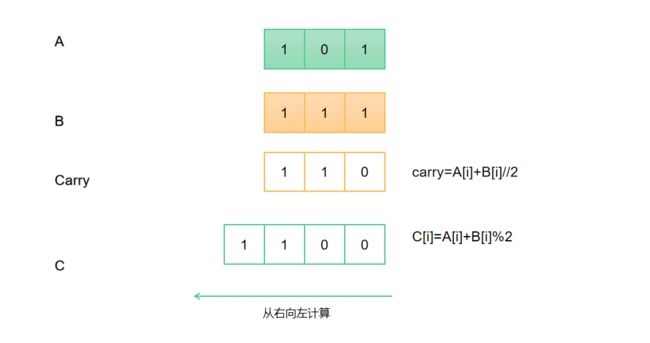
    print("关键字%s对应的索引是: %s" %(find_key, key_index))

• 执行结果如下
  
• 循环不定式: 循环迭代访问子串A[1…i-1]不包含元素v。
  • 初始化
  • 保持
  • 终止

1-4. 考虑把两个n位二进制整数加起来的问题，这两个整数分别存储在两个n元数组A和B中。这两个整数的和应按二进制形式存储在一个(n+1)元数组C中。请给出该题的形式化描述，并写出伪代码。

• 形式化描述

  • 输入: 数组A=和数组B=
  • 输出: 数组C=

• 解题思路: 逐位计算法
  carry存储是否需要进位， 1代表需要，0代表不需要。
  

• 伪代码

ADD-BINARY(A, B)
    C = new integer[A.length + 1]
    carry = 0
    for i =  A.length to 1
        C[i+1] = (A[i] + B[i] + carry) % 2  		// remainder
        carry = (A[i] + B[i] + carry) / 2 		// quotient
    C[0] = carry					//第一位根据carry判断是否需要进位					
    return C

• Python代码

def add_binary(A, B):
    """二进制相加，此处A和B位数相等"""
    length = len(A)
    # 是否进位
    carry = 0
    # 二进制相加结果存储
    C = [0] * (length + 1)
    # 长度为3时，索引分别为2, 1, 0
    for index in range(length - 1, -1, -1):
        C[index+1] = (A[index] + B[index] + carry) % 2
        carry = (A[index] + B[index] + carry) // 2
    C[0] = carry
    return  C

if __name__ == '__main__':
    A = [1, 0, 1]
    B = [1, 1, 1]
    C = add_binary(A, B)

    print('A: ', A)
    print('B: ', B)
    print("数组A和数组B二进制相加结果为: ", C)

• 执行效果如下:
  

• 题目拓展: 书本上的练习题A和B位数相等，那如果位数不相等呢?可参考Leetcode编程题67. Add Binary

2. 分析算法练习

2-1. 用theat记号表示函数n³/1000-100n²-100n+3
解答: theat表示，只考虑公式中的最重要的项，当n的值很大时，低阶项相对来说不太重要。
theta(n)=n³
2-2. 选择排序

• 伪代码

n = A.length
for i = 1 to n - 1
    minIndex = i
    for j = i + 1 to n
        if A[j] < A[minIndex]
            minIndex = j
    swap(A[i], A[minIndex])

• Python程序代码

def select_sort(A):
    """
    选择排序
    1. 找出A中最小的元素和A[1]交换
    2. 找出A中第二小的元素和A[2]交换
    ......
    3. 找出A中的倒数第一小的元素和A[n]交换
    """
    n = len(A)
    for i in range(n-1):
        minIndex = i
        for j in range(i+1, n):
           if A[j] < A[minIndex]:
               minIndex = j
        # swap(A[i], A[minIndex])
        A[i], A[minIndex] = A[minIndex], A[i]
    return  A

if __name__ == '__main__':
    A = [1, 31, 41, 59, 26, 41, 58]
    sort_A = select_sort(A)
    print("数组排序结果: ", sort_A)