unity初识之Quaternion和旋转

与之前做2d游戏不一样，3d游戏中，角度变换，用四元数来表示和计算

什么是欧拉角

四元数

欧拉旋转

一个女生的文章

unity对于四元数的定义

在学习3d数学或者学习shader的书籍里，都会有一章是先学下向量，矩阵的知识。矩阵的几何意义是变换，几种变换里用的多的也是unity的Transform组件中用到的：平移，旋转(rotation)，缩放(scale)。
缩放和旋转是一个线性变换(Linear transform ) ，指那些可以保留矢量加和标量乘的变换 数学公式表示可以是 f(x) + f(y) = f(x+y) kf(x) = f(kx)
平移是一种非线性变换。

旋转是其中最为复杂的一种。

要表示一个物体的方位，最少得有三个数来表示，两个数只能表示一个方向。而且描述物体的方位时，不能使用绝对量，与位置只是相对于某个已知点(比如坐标系原点)的位移一样，方位时通过相对已知方位的旋转来描述的，旋转的量叫做角位移。之前做的游戏里，也是整个游戏世界有个坐标系，以它的原点为基础，有各自物体的位置，旋转相对于坐标原点的描述。然后物体内的孩子又以物体的位置作为坐标系的原点，描述自己的状态。

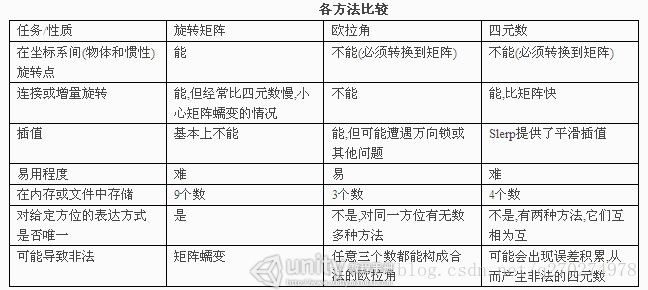
描述坐标系中方位的方法

### - 矩阵形式。

比如3x3矩阵，第一行代表 x方向的x , y z 值， 第二行代表y方向的，第三行表示z方向的，三行一起可以表示该物体所处的方位。
优势是:
可以立即进行向量的旋转。其他描述方式做不到。
矩阵的形式被图形api所使用。 也就是不管程序里用什么方式来表示方位旋转，最后在底层或者显卡那交互的都是矩阵。类似很多游戏引擎会让开发者用不同的语言来写逻辑，比如Untiy可以用unity-javascript和c# ，但编译后会变成IL语言，egret里用TypeScripte写逻辑，编译后都会转成javascript代码。ts比js多了面向对象的内容，更方便些，灵活性更高。
多个角位移连接，我理解为可以在两个坐标系之间转换只能使用矩阵，而在程序中描述和存贮如果用别的形式的话，最后在转换坐标系的时候，只有都变成矩阵来操作。
矩阵的逆，旋转矩阵是正交的，如果想求角位移的反向，直接用矩阵的转置就可以求得了，不用计算矩阵的逆了。

 缺点是：
 矩阵占据更多内存。3x3矩阵，就是9个数，代表一个方位，如果是动画的话，一帧中如果做旋转操作，并且算上骨骼旋转，皮肤旋转，量很大，何况一个动画会有很多帧。
 难于使用。矩阵是用的向量，都是-1到1之间的值，人类平时描述都是角度。
 矩阵可能是病态的，可能有冗余。

### - 欧拉角形式。

 基本思想是将角位移分解为绕三个互相垂直轴的三个旋转组成的序列。用欧拉角是有顺序的，比如untiy中，x,y,z分别为right,up，forward 。  也就是比如旋转一个x , y ,z都转的角度，是先转一个，再转一个，再转最后一个。如果顺序改变，有可能最后的结果是不一样的(例子******)。     具体欧拉角顺序是什么，有个约定叫 “heading,pich,bank”，也就是Untiy中对应的约定，heading 也就是up,y轴，    pich就是right  x轴，   bank就是 forward,z轴。
 ![这里写图片描述](https://img-blog.csdn.net/20180302193130776?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvcTI3MDI3NDk3OA==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70) 
  优点:
 使用容易，使用的参数全都是角度的形式。在cocos和egret这些2d引擎中，之前做2d游戏，设置rotation也是直接就用的角度。
 最简洁的表达。3d中描述一个方位，不能少于3个数，欧拉角只有3个。
 任意三个数都是合法的。

缺点：
给定方位的表达不唯一(举例**)。 最简单的一种，一个角度加360°的倍数，虽然最终表现的方位没有变，但是数值变了。第二种，x,y,z的分别的旋转角度相互作用后，后影响最后的结果。比如，x轴转135度， 就跟y转180度，x转45度，z转180度结果显示一样。规避的方法是，限制传入的角度的范围来保证某一个方位是独一无二的。
另一个问题就是，万向锁 (一个对万向锁的解释http://v.youku.com/v_show/id_XNzkyOTIyMTI=.html) 不可避免
两个角度求差值困难。也是两个问题。第一个没有限制角的情况下，比如720° 和45°的差值，其实只有从0°到45°，但是却相当于绕了将近两圈。

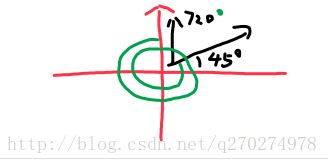
第二个就是在限制角的情况下会按照远的算，而不是按进的算，比如，角度限制在-180到+180之间，-170°和170°之间，其实在第三象限和第四象限只差了20°，蛋有可能从另一个方向算了。

### - 四元数形式
包括一个向量v和一个标量w，
[w, v] , [w,(x,y,z)]

 优点:
 平滑差值: 用slerp可以得到平滑的转角度的差值
 快速连接和角位移求逆，四元数叉乘能将角位移序列转换成单个角位移。
 能和矩阵快速转换。
 仅用4个数。比矩阵强点，比欧拉角多一个。

获得一个轴-角对，3d中的任意角位移都能表示为单一轴的单一旋转，用这种形式来描述的称为轴角描述法。是除了矩阵，欧拉角，四元数外的第四种表示法。

---

Unity中 Quaternion类的理解与使用
https://docs.unity3d.com/ScriptReference/Quaternion.html

上面说了三种方位的表示方式。untiy中，使用了四元数来表示rotations. 也是因为上面说过的四元数相比较其他表示方式的优点，简洁，只有四个数就能表示一个方位，避免了gimbal lock 万向锁，并且很容易就可以求得差值。
缺点也是上面提到的，复杂不直观，估计咋们用的人几乎是不会单独访问或者修改Quaternion的4个组件了。几乎大部分是通过已有的rotations去构造新的rotations.（比如两个rotations间平滑的变换的差值）.估计开发者99%会用到的是Quaternion.LookRotation, Quaternion.Angle, Quaternion.Euler, Quaternion.Slerp, Quaternion.FromToRotation, and Quaternion.identity. 这几个函数。。。
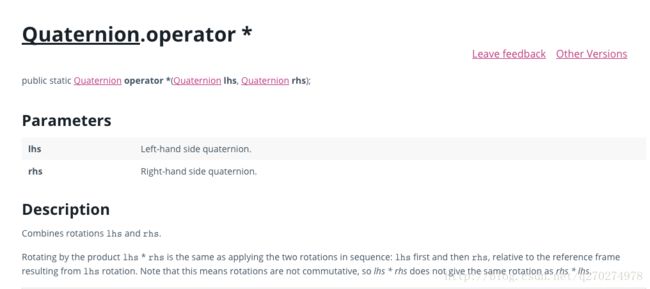
可以用Quaternion重载的* 操作符，通过一个rotation就行旋转，或者旋转一个向量。
刚才看到的四元数的优点也有，四元数的叉乘可以将多个角位移的序列变成一个的变化。

https://www.youtube.com/watch?v=TdjoQB43EsQ&t=104s 官方的一个演示视频

下面就挨个把各个工具函数的用法以及变现结果试一遍

---

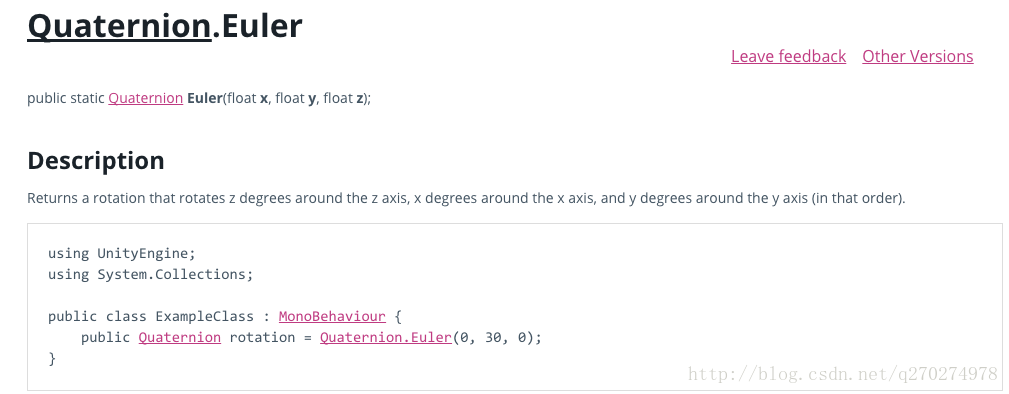
归一化的处理，就是把rotation改成 欧拉角表示为(0,0,0)
预先设置为60°

public class ExampleClass : MonoBehaviour {
    void Example() {
        transform.rotation = Quaternion.identity;
    }
}

结果

---

返回欧拉角代表的角度。就是把四元数转成欧拉角

public Quaternion rotation = Quaternion.identity;
    void Example() {
        rotation.eulerAngles = new Vector3(0, 30, 0);
        print(rotation.eulerAngles);
    }

结果是 (0.0, 30.0, 0.0)

---

通过开始位置到终点位置来创建一个rotation.

比如做了这些绑定, 每一帧都平滑的设置位移，并且根据当前帧的位移，转一下物体，最后效果是物体转着圈的转到了目标位置

//This is the Transform of the second GameObject
    public Transform m_NextPoint;
    Quaternion m_MyQuaternion;
    float m_Speed = 1.0f;

    void Start()
    {
        m_MyQuaternion = new Quaternion();
    }

    void Update()
    {
        //Set the Quaternion rotation from the GameObject's position to the next GameObject's position
        m_MyQuaternion.SetFromToRotation(transform.position, m_NextPoint.position);
        //Move the GameObject towards the second GameObject
        transform.position = Vector3.Lerp(transform.position, m_NextPoint.position, m_Speed * Time.deltaTime);
        //Rotate the GameObject towards the second GameObject

        transform.rotation = m_MyQuaternion * transform.rotation;

        Debug.Log(transform.rotation.eulerAngles);
    }

---

这里是获得一个轴-角对，3d中的任意角位移都能表示为单一轴的单一旋转，用这种形式来描述的称为轴角描述法。是除了矩阵，欧拉角，四元数外的第四种表示法。只是很少用到据说。

unity editor中预设值

    public float angle = 0.0F;
    public Vector3 axis = Vector3.zero;
    void Example() {
        transform.rotation.ToAngleAxis(out angle, out axis);
        Debug.Log(" angle is  " + angle);

        Debug.Log(" axis is  " + axis);
    }

输出
angle is 64.38145 axis is (0.6, 0.8, 0.0) 还没明白为啥。。。不过也不会常用吧。

---

字符串打印

print(Quaternion.identity);

输出 (0.0, 0.0, 0.0, 1.0)

---

两个四元数间的角

public Transform target;
    void Update() {
        float angle = Quaternion.Angle(transform.rotation, target.rotation);
          Debug.Log(angle);
    }

原角是（0，60，0） target角是 (0,30,0)
输出是 30

---

两个四元数进行点积 ，（四元数点乘类似于向量的点乘的几何解释，绝对值越大，两个rotations代表的角位移越相似。感觉可以用来判断两个旋转，基于某个旋转，谁转的厉害。。。）

---

应该是比较常用的方式，将欧拉角转化为四元数，然后可以进行旋转。

---

创建一个从开始方向到结束方向的旋转 (0,0,0)

void Awake() {
        print(transform.forward);
        transform.rotation = Quaternion.FromToRotation(Vector3.up, transform.forward);
        print(transform.rotation.eulerAngles);

这个是从 (0,1,0)方向 转到 (0,0,1) 得到的结果是 (90,0,0) 绕x轴转90度的旋转

---

返回一个相反的旋转

void Awake() {
transform.rotation = Quaternion.Inverse(transform.rotation);
        print(transform.rotation.eulerAngles);
}

预先转的是 (0,60,0)

inverse之后是 (0,300,0) 也就是 (0,-60,0)

---

线性插值( Linear Interpolation)
计算角度ab间的差值，并且之后规范结果，参数t是在0到1之间。
lerp比slerp快 但是如果旋转角度离得远看起来会很糟糕。

---

球面线性插值(Spherical Linear Interpolation)基本思想是沿着4d球面上连接两个四元数的弧度值.

---

创建一个指定的forward 和upward方向的旋转
返回一个计算的四元数，如果用来确定一个transform , z轴将和forward对齐，y轴将和upward对齐，如果向量是正交的。如果forward方向是0将会报错。

比如

public Transform to;
void Awake() {
        Vector3 relativePos = to.position - transform.position;
Quaternion rotation = Quaternion.LookRotation(relativePos);
transform.rotation = rotation;
        Debug.Log(transform.rotation.eulerAngles);
        Debug.Log(relativePos);

小人的锚点位置会一直看向蓝点

https://www.youtube.com/watch?v=nJiFitClnKo 一个视频演示

---

旋转一个旋转 从from 到 to ，但是角速度不能超过最大值。 如果maxDegreesDelta是个负值，那他会一直远离to的角度，直到到了相反的方向

合并两个旋转，但是不满足交换律。四元数的乘法不满足交换律