深度学习中的卷积和池化

1. Convolution

卷积是什么？

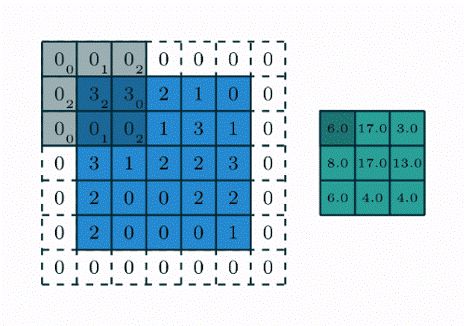
卷积在数学上用通俗的话来说就是输入矩阵与卷积核（卷积核也是矩阵）进行对应元素相乘并求和，所以一次卷积的结果的输出是一个数，最后对整个输入输入矩阵进行遍历，最终得到一个结果矩阵，下面通过一个动画使其更直观。

• 卷积动画演示
  
  • 卷积核
    

在上面我们没有使用很专业的数学公式来表示，来解释卷积操作和相关操作，我结合我自己的理解，争取做到白话，及时没有数学基础，也能理解卷积核池化操作。

• 卷积的目的

卷积在图像中的目的就是为了提取特征，我认为这就是深度学习的核心，因为有了卷积层，才避免了我们来手动提取图像的特征，让卷积层自动提取图像的高维度且有效的特征，虽然这没有手动提取特征比如Canny边缘，SIFT，HOG等的强大数学理论基础的支撑，但是卷积层提取的特征让最终的分类、识别结果往往非常的好。比如LeNet-5模型能在MNIST数据集上达到99%的识别率，一般来说网络结构越复杂，越深，往往最终的精确率会越高。

---

卷积分为许多种，下面将会一一介绍。

• 符号约定

i: 输入大小表示为i*i

k: 卷积核大小表示为k*k

s: 步长

p: 填充

o: 输出表示为o*o

1.1 unit strides

卷积从大体上可以分为单位步长（unit strides)和非单位步长（Non-unit strides），还可以细分为有0填充和无0填充。

1.1.1 No zero padding, unit strides

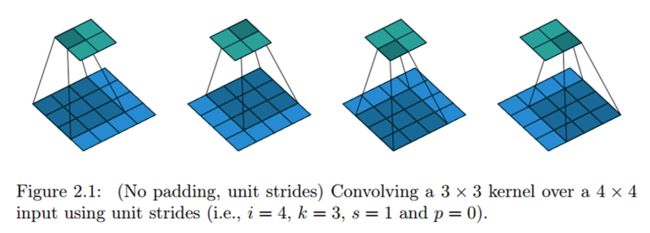
无零填充 单位步长的卷积，蓝色矩阵是输入（4x4）,深蓝色是卷积核（3x3）,上方绿色是输出（2x2）.输出矩阵大小的计算公式为：

动画演示

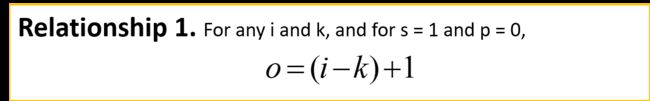
1.1.2 Zero padding, unit strides

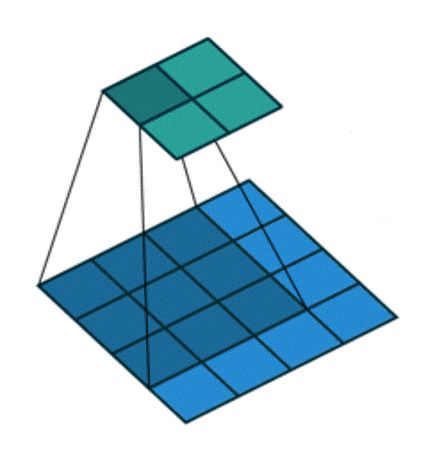
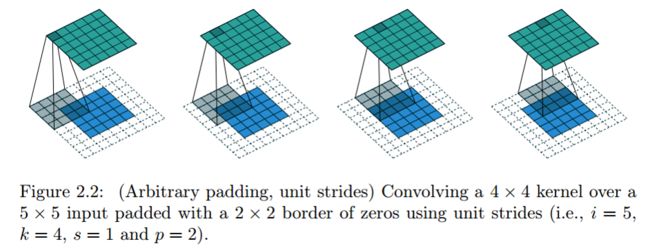
有零填充（p=2） 单位步长的卷积，蓝色矩阵是输入（5x5）,深蓝色是卷积核（3x3）,上方绿色是输出（6x6）.输出矩阵大小的计算公式为：

动画演示

1.1.2.1 Zero padding, unit strides - Half(Same) padding

这种情况叫Half Padding 也叫 Same Padding，因为它能保证输入和输出的尺寸是一致的

有零填充（p=1） 单位步长的卷积，蓝色矩阵是输入（5x5）,深蓝色是卷积核（3x3）,上方绿色是输出（5x5）.输出矩阵大小的计算公式为：

动画演示

1.1.2.2 Zero padding, unit strides - Full padding

卷积操作产生的输出一般都会减少输入图片的尺寸，但有时候我们需要放大输入图片的尺寸，这个时候就需要使用到Full Padding。

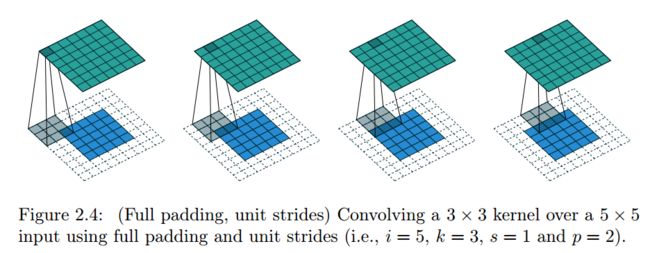
有零填充（p=2） 单位步长的卷积，蓝色矩阵是输入（5x5）,深蓝色是卷积核（3x3）,上方绿色是输出（7x7）.输出矩阵大小的计算公式为：

动画演示

1.2 Non-unit strides

接下来介绍非单位步长（Non-unit stride)的卷积操作，分为有零填充和无零填充。

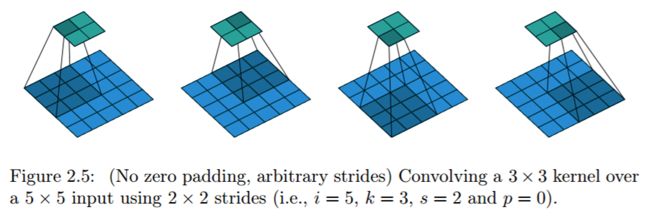
1.2.1 No zero padding, non-unit strides

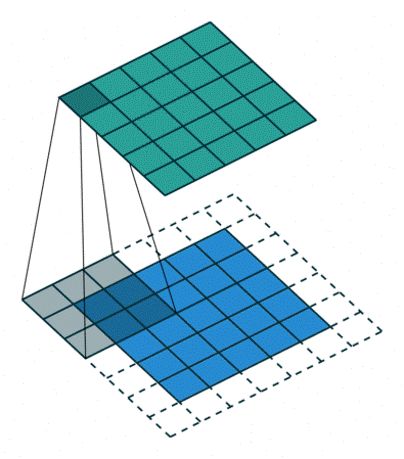
无零填充 非单位步长（s=2）的卷积，蓝色矩阵是输入（5x5）,深蓝色是卷积核（3x3）,上方绿色是输出（2x2）.输出矩阵大小的计算公式为：

其中向下取整是为了避免(i-k)/s是小数的情况。

动画演示

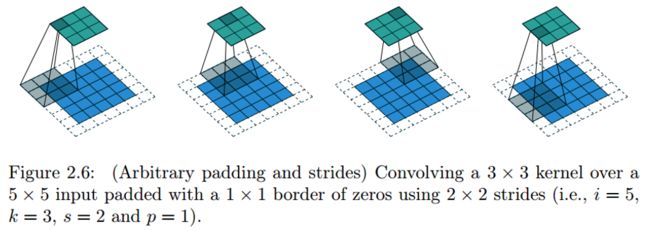
1.2.2 Zero padding, non-unit strides

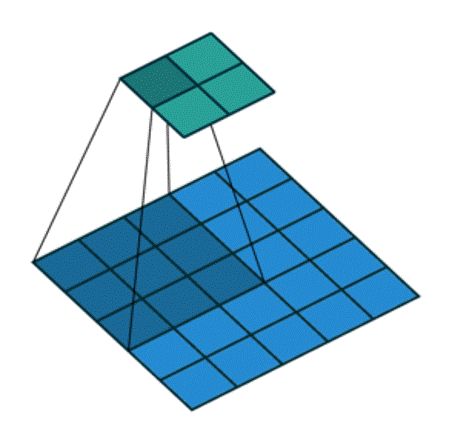
有零填充（p=1） 非单位步长（s=2）的卷积，蓝色矩阵是输入（5x5）,深蓝色是卷积核（3x3）,上方绿色是输出（3x3）.输出矩阵大小的计算公式为：

其中向下取整是为了避免(i+2p-k)/s是小数的情况。

动画演示

1.3 Convolution as a matrix operation

卷积操作也可以被表示为矩阵的形式，比如将1.1.1中的图转化为矩阵，如下图所示：

1.1.1中的图被表示为如下形式

矩阵表示的形式

我将上面的矩阵划分为了4行，每一行划分为了4列，表示此卷积操作需要进行16次，W0,0 W0,1 …… W2,2我在图中标注了出来。这个矩阵可以这样来看，按行来看，第一行对应于矩阵表示图的第一个图，第二行对应于矩阵表示图的第二个图，一次类推。

2. Pooling

池化操作是什么？

池化操作的过程和卷积很类似，但是卷积是用来提取特征的，池化层是用来减少卷积层提取的特征的个数的，可以理解为是为了增加特征的鲁棒性或者是降维。

池化分为平均值池化和最大值池化，下面会一一介绍。

2.1 Average Pooling

• 平均值池化可以被表示为

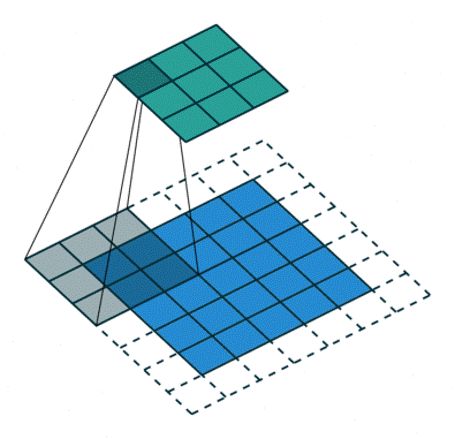
• 平均值池化的动画演示

可以看到池化操作也有一个类似于卷积的核，但是这个核不需要提供值，只是表示一个能作用于输入图片的窗口大小。

2.2 Max Pooling

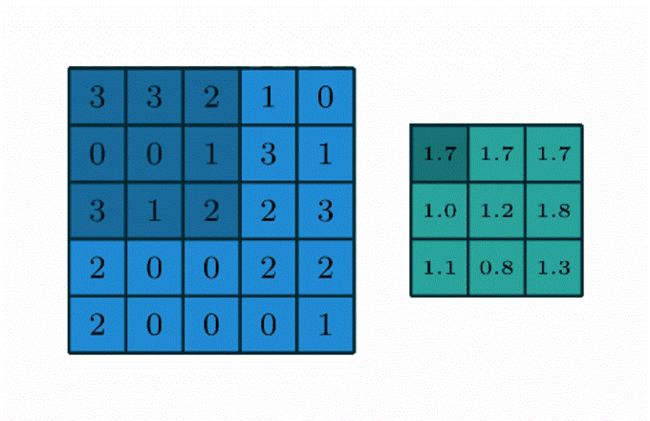
• 最大值池化可以被表示为

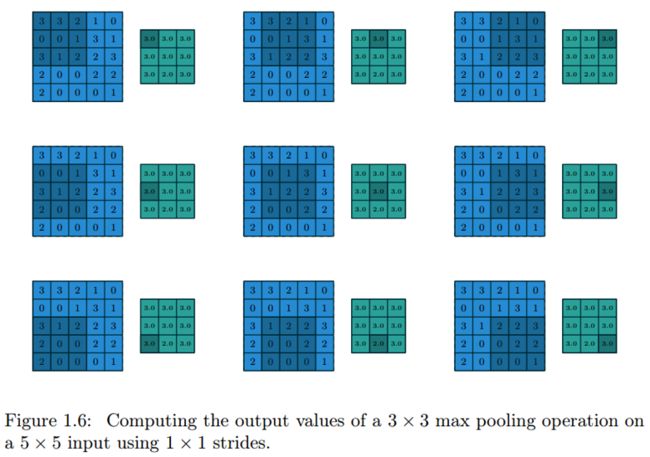
• 最大值池化的动画演示

可以看到池化操作也有一个类似于卷积的核，但是这个核不需要提供值，只是表示一个能作用于输入图片的窗口大小。

3. 3D-Conv

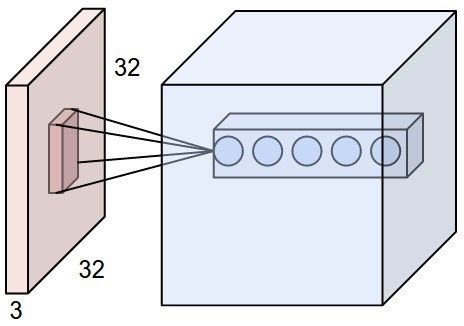
3维的卷积，我个人的简单理解，就是在2维卷积的基础上加了一个深度的概念，如图。

输入是一个32x32x3的矩阵，卷积核假定是5x5x3，可以看到一次的卷积操作的结果就是一个带有深度的单位矩阵（2维的一次卷积操作的结果是深度为1的单位矩阵）。这里的深度可以自己指定。

为了更好的理解3维的卷积，这里引用斯坦福写的一篇博客里面的动画。http://cs231n.github.io/convolutional-networks/

width="”100%”" height="”100%”" src="”https://cs231n.github.io/assets/conv-demo/index.html”" allowfullscreen="">

4. LeNet-5

这里介绍下LeNet-5模型，为了理解前面讲述的各种模型

Bibliography