LeetCode专项练习之双指针（Two Pointers）笔记

关于Leetcode的专项练习建议，可去查看知乎大佬的文章（https://zhuanlan.zhihu.com/p/104983442）。

今天的笔记包含双指针（Two Points）类型下的9个题目，它们在leetcode上的编号和题名分别是：

• 1 - Two Sum 
• 15 - 3Sum 
• 16 - 3Sum Closest
• 259 - 3Sum Smaller
•  844 - Backspace String Compare
•  26 - Remove Duplicates from Sorted Array
•  75 - Sort Colors
•  977 -  Squares of a Sorted Array
•  713 - Subarray Product Less than K

下面将根据以上顺序分别记录代码和对应心得，使用的编译器为Python3。

---

Two Sum

这是每个初次接触leetcode的同学都将做的第一道题。题目本身的思维方式十分简单，可采用暴力破解法，利用for循环嵌套，便可通过测试：

class Solution:
    def twoSum(nums: list, target: int) -> list:
        newlist = []
        for firstIndex in range(0, len(nums)-1):
            for secondIndex in range(firstIndex+1, len(nums)):
                if nums[firstIndex] + nums[secondIndex] == target:
                    newlist.append(firstIndex)
                    newlist.append(secondIndex)
                    return newlist

两个for循环在我看来便是对双指针的初级用法。但显然，这里的双指针并不高效（O(n^2)），仅仅是作为一个启蒙式的运用而已。

因此，在查阅了解题技巧之后，我发现使用Python的字典进行哈希查询更加便利和巧妙：

class Solution:
    def twoSum(nums: list, target: int) -> list:
        # 构建字典
        dic = {}

        # 利用枚举将列表的数据和对应下标进行存储，注意存储方式（并非死板的使用"index -> value"来存储）
        for index, value in enumerate(nums):
            dic[value] = index

        for requiredIndex1, value in enumerate(nums):
            # 灵活运用字典的get方法，获得相应索引
            requiredIndex2 = dic.get(target - value)
            if requiredIndex2 is not None and requiredIndex1 != requiredIndex2:
                return [requiredIndex1, requiredIndex2]

自己以前用字典类型去存储列表时，一味地把列表下标当作key进行存储，导致get永远只能get到下标的对应的字符，从未想过反向存储，灵活运用get方法，通过字符去寻找对应下标。此外，enumerate这个方法也值得记录，它对一次性遍历列表的字符和对应下标非常有用。

---

3Sum 

个人感觉这道题十分有价值。它不仅让我第一次觉得双指针运用竟然是如此高效，还进一步考察了关于边界条件和重复值过滤的问题。

第一次我尝试着利用三层for循环嵌套去通过测试，结果发现超时（在Python上运用暴力破解，效率极低，容易超时）；第二次我尝试着去寻找规律，利用“两数之和必为第三数的相反数”，减少复杂度，使第三个数更容易被定位。但仍旧超时，且边界条件没能理清。

于是，在参考了解题思路后，我发现利用双指针（严格上来讲是3个指针，只不过第一个指针仅仅是用来遍历列表）更有效。核心思路是：将排序好的列表进行遍历，每次遍历时便设置两个额外指针位于当前遍历指针的前面（i+1）和列表尾部。同时，通过比对三个指针的数字之和（可能不用三个）和左右指针是否相碰，来确定是移动左指针，右指针还是进入下一循环。

class Solution:
    def threeSum(self, nums: list) -> list:
        # 预先排序处理➕双指针。此题移动双指针两端的规律：三数之和大于0，说明右边的数更大，右指针向左移；
        # 3数之和小于0，说明左边的数更小，左指针右移。终止条件除了左指针>=右指针，还得考虑遍历时i的大小（若i >= 0，那三数之和肯定大于0）
        # 过滤重复答案：当任意指针移动后发现"指针对应的值"等于移动前的值，继续移动
        if len(nums) < 3:
            return []
        nums.sort()
        result = []
        print(nums)
        for i in range(len(nums)):
            if nums[i] > 0:
                break
            if i > 0 and nums[i] == nums[i-1]:
                continue
            m = i + 1
            n = len(nums) - 1

            while m < n:
                answer = nums[i] + nums[m] + nums[n]

                if answer > 0:
                    # 因为三数之和大于0，并且右指针对应数字最大，所以仅移动右指针
                    n -= 1
                    # 排除重复元素
                    while nums[n+1] == nums[n] and n > m:
                        n -= 1
                elif answer < 0:
                    # 因为三数之和小于0，并且左指针对应数字最小，所以仅移动左指针
                    m += 1
                    # 排除重复元素
                    while nums[m-1] == nums[m] and n > m:
                        m += 1
                else:
                    result.append([nums[i], nums[m], nums[n]])

                    # 等于0，即同时移动两个指针（若相碰则移动第三个指针，进入下一循环）
                    n -= 1
                    while nums[n+1] == nums[n] and n > m:
                        n -= 1
                    m += 1
                    while nums[m-1] == nums[m] and n > m:
                        m += 1

        return result

---

3Sum Closest

在吸取了“3Sum”的经验之后，解决“等于0”和解决“最接近某数字”的问题是十分相似的。因此，我在做这道题时直接套用了做“3Sum”的思路，利用排序+双指针的方法很快就通过了测试。唯一不同便是每次需要将得到的三数之和与当前最接近的值进行比对，并取最优值。

import sys

class Solution:
    def threeSumClosest(self, nums: list, target: int) -> int:
        # 双指针思路，同“3Sum”
        if len(nums) < 3:
            return None
        res = sys.maxsize
        nums.sort()
        for i in range(len(nums)):
            # 定义双指针
            m = i + 1
            n = len(nums) - 1

            while m < n:
                cur = nums[i] + nums[m] + nums[n]

                # 对比当前结果和已记录的最优结果
                if abs(res-target) > abs(cur-target):
                    res = cur

                # 移动对应指针
                if cur > target:
                    n -= 1
                    while nums[n] == nums[n+1] and m < n:
                        n -= 1
                elif cur < target:
                    m += 1
                    while nums[m] == nums[m-1] and m < n:
                        m += 1
                else:
                    return cur

        return res

---

3Sum Smaller

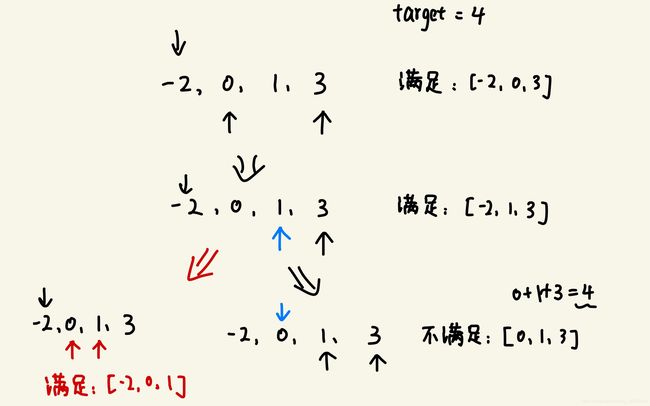
本来我以为这道题与“3Sum”，“3Sum Cloest”十分类似，想着套用同样的双指针思路便可以解决，但我想的太简单了。在这道题里，有一个关键的点是：什么时候移动哪一个指针。在以往的题里，通过比对三数之和大于或小于target，便可轻松判断移动哪个指针。但在这题，三数之和大于target还好，知道是左移右指针；但如果小于target呢？若使左指针右移，确实可以满足题意，小于target的子集数量会随着左指针的移动而更新，但这样会遗漏一定数量的子集。例如：

如图，如果在sum < target时仅选择记录并右移左指针的话，会遗漏掉右指针左移产生的新子集[-2, 0, 1]。因此，在sum < target时，不能单纯只记录当前数据和移动左指针，毕竟移动右指针也可以满足要求。于是，我当时便卡在了如何去移动指针这个节骨眼上。在查看题解后，我才明白自己想的太死板：一旦sum < target，说明nums[right]之前的所有三数之和都满足条件啊，不是已经排序了吗！所谓当局者迷，旁观者清。是自己想的过于狭隘，这么简单的一个逻辑都没发现。所以，当sum < target时，不是去计数当前的子集，而是去计数所有从nums[left]到nums[right]之间的个数，再右移左指针：

class Solution:
    def threeSumSmaller(self, nums: list, target: int) -> int:
        # 双指针。用一个for循环遍历列表，双指针始于循环指针i之后的表头（i+1）和表尾（len-1）。利用三数相加比对target，
        # 如果小于则说明右边指针到左指针内的所有数字（right-left）相加都可以小于target。另外，根据与差值的比较结果（大于/小于）来移动
        # 对应指针
        nums.sort()
        if len(nums) < 3:
            return 0
        nums.sort()
        res = 0

        for i in range(len(nums)-1):
            # 定义指针
            m = i + 1
            n = len(nums) - 1
            while m < n:
                cur = nums[i] + nums[m] + nums[n]
                if cur >= target:
                    n -= 1
                else:
                    # 因为nums[n]是当前最大的数字，所以所有在nums[n]之前的数进行三数相加都将小于target
                    res += n - m
                    m += 1

        return res

---

Backspace String Compare

这道题理解起来比较简单，但在做的时候需要注意多个“#”出现时会发生什么。我的两种思路都是通过构建新的字符串来进行比较。

第一种是先把字符串转换为列表（字符串在Python不支持多次删减），并采用正向遍历的方法，遇到多少个“#”就把之前多少个非“#”字符串转化为“#”，最后在向新字符串添加列表内容时，过滤掉“#”字符：

class Solution:
    def backspaceCompare(self, S: str, T: str) -> bool:
        # 转化为list再遍历,遇到多少个连续的#就把左边对应的多少个非#字符替换为#，最后用字符串加上非#字符
        newS = list(S)
        newT = list(T)

        for i in range(len(newS)):
            if newS[i] == "#":
                j = i-1
                while newS[j] == "#" and j > -1:
                    j -= 1
                if j > -1:
                    newS[j] = "#"
        S = ""
        for element in newS:
            if element != "#":
                S += element

        for i in range(len(newT)):
            if newT[i] == "#":
                j = i - 1
                while newT[j] == "#" and j > -1:
                    j -= 1
                if j > -1:
                    newT[j] = "#"

        T = ""
        for element in newT:
            if element != "#":
                T += element

        return S == T

这种做法虽然能通过测试，但耗时过多。除了进行多次str->list操作以外，逻辑也较为复杂，需要顾及更多边界条件，稍不注意就容易漏掉。

于是通过解析，我进行了改良，通过单指针逆向扫描字符串，遇到多少个“#”就跳过多少个非“#”字符串的录入，逻辑清晰，无需进行字符串转换和考虑过多边界条件：

class Solution:
    def backspaceCompare(self, S: str, T: str) -> bool:
        # 单指针（逆向扫描）。观察题目，可发现规律如下：字符串从右往左看（逆向思维），遇到多少个#就跳过多少个#之后的非#
        # 字符串。相比正向遍历，逆向遍历可以轻松避免"遇到多个#符号时如何去掉之前已经添加过的字符"的问题。同时逆向添加字符串并不影响比对
        # 最后的结果（反正只返回true/false，不用管删除后字符串是什么样子）
        newS = ""
        newT = ""
        count = 0
        for i in range(len(S)-1, -1, -1):
            if S[i] == "#":
                count += 1
                continue
            elif count != 0:
                count -= 1
                continue
            else:
                newS += S[i]

        count = 0
        for i in range(len(T)-1, -1, -1):
            if T[i] == "#":
                count += 1
                continue
            elif count != 0:
                count -= 1
                continue
            else:
                newT += T[i]

        return newS == newT

最后同样通过了测试，但耗时缩短了接近一半。

---

Remove Duplicates from Sorted Array

在O(1)复杂度下实现，说明需要靠指针来指出并排除重复元素。此题我也使用了两种方法。

第一种方法比较蠢，但行得通。核心思想也是基于双指针：通过扫描列表元素，把重复的元素删除之后又添加到尾部上去，直到遍历到原列表的长度（一开始指定）为止：

class Solution:
    def removeDuplicates(self, nums: list) -> list:
        # 双指针
        tail = len(nums)-1
        # 遍历列表，从1开始
        for i in range(1, len(nums)):
            while nums[i] == nums[i-1] and i <= tail:
                cur = nums[i]
                # 删除又添加
                nums.remove(nums[i])
                nums.append(cur)
                
                # 添加后原来的尾指针不再指向最大值，所以需要-1
                tail -= 1

        return nums

但不断地删除又添加元素会消耗更多资源，进而影响整体效率。

第二种方法同样也是双指针，但采用了快慢指针的形式，正向扫描列表。一旦nums[fast] > nums[slow]，便右移慢指针，同时替换掉nums[slow]，直到快指针到达数组长度（快指针用于遍历，慢指针用于定位非重复子集的长度）：

class Solution:
    def removeDuplicates(self, nums: list) -> list:
        # 大佬 solution: 双（快慢）指针。通过一个快指针迅速遍历，在遇到比慢指针对应的数值更大的数后，用大数替换掉慢指针对应数据，慢指针继续前进
        # 如果遇不到则说明重复了，毕竟列表是已经排好序的
        index = 0
        j = index + 1
        while j < len(nums):
            # because it is sorted, compare the value and replace duplicated values
            if nums[index] < nums[j]:
                index += 1
                nums[index] = nums[j]
            j += 1

        return nums

---

Sort Colors

此题又被称为“荷兰旗”问题，要求使用O(1)空间实现数组（列表）排序。若不考虑时间复杂度，暴力双循环当然可以很快写出来并通过测试（然而对Python编译不实用）。因此，降低时间复杂度和仅使用O(1)空间便是关键。

在查看了解析后，我发现双指针的用法其实十分广泛。解析首先仍旧定义三个指针：一个位于左（头），一个位于尾（右），一个用于遍历列表。与以往不同的是，在这里，左指针指向的数代表第一个非“0”数字，右指针则是代表第一个非“2”数字。当遍历指针指向的数是“0”时，将nums[i]与nums[left]进行交换，同时右移遍历指针；当指向的数字为“1”时，只右移遍历指针；当指向的数字为“2”时，交换nums[i]与nums[right]，但此时不再移动遍历指针，而是进入下一个循环。原因很简单：nums[right]原来的值是未知的，交换后的nums[i]是否满足nums[i]与nums[left]交换的条件（等于0），需要再判断后才知道：

class Solution:
    def sortColors(self, nums: list) -> None:
        """
        Do not return anything, modify nums in-place instead.
        Follow up: use constant space only: O(1)
        """
        # 三指针：一个用于遍历，两个位于头尾（0，len(n-1)）。位于头指针之前的数被认定为0，尾指针之后的数
        # 被认为2。当遍历指针对应值为0时，交换头指针和当前指针的值，头指针和当前指针均右移；当对应值为1时，右移当前指针；
        # 注： 当值为2时，交换当前指针和尾指针的位置，尾指针左移，但当前指针不移动，直接进入下一循环，直到当前指针等于尾指针为止。
        # （因为不确定交换过后当前指针对应的值是什么，需要再判断）
        cur = 0
        m = 0
        n = len(nums) - 1
        while cur <= n:
            # 左
            if nums[cur] == 0:
                temp = nums[cur]
                nums[cur] = nums[m]
                nums[m] = temp
                m += 1
                # 重要!
                cur += 1
            # 右
            elif nums[cur] == 2:
                temp = nums[cur]
                nums[cur] = nums[n]
                nums[n] = temp
                n -= 1
            # 重要!
            else:
                cur += 1

---

Squares of a Sorted Array

此题的题意也十分容易理解，在阅读完之后我立刻就想到了一些排序算法和绝对值比较的知识点。于是我便马上用冒泡算法和绝对值排序来迅速解决问题，结果却显示超时……

class Solution:
    def sortedSquares(self, A: list) -> list:
        # Bubble sort：冒泡排序➕绝对值比较换位——超时
        for i in range(len(A)):
            hasAction = False
            # 减去i是为了省去指针指到已排好序的值的情况(已经冒泡的值)
            for j in range(len(A)-i-1):
                pre = abs(A[j])
                next = abs(A[j+1])
                if pre > next:
                    temp = pre
                    A[j] = next
                    A[j+1] = temp
                    hasAction = True
            # 如果第一次循环都没任何泡，终止（已经排好序）
            if not hasAction:
                break

        # 列表内对应数字相乘
        return list(map(lambda x, y: x * y, A, A))

或许是返回时为了让列表内数字平方，还使用了Lambda函数（觉得循环比较耗时）。起码，使用冒泡算法在这里是会显示超时的。考虑到这是专项练习，我便马上思考用双指针来解决。

最后发现，因为列表是已经排好序的，所以正数和负数各自也一定是排好序的。那么在处理负数的顺序问题时，可以用一个指针逆向扫描列表并标记到第一个负数，再用另一个指针指向负指针+1的位置，代表第一个非负数。最后仅需合并两个指针各自指向的数就行了：

class Solution:
    def sortedSquares(self, A: list) -> list:
        res = []
        i = 0
        while i < len(A) and A[i] < 0:
            i += 1
        j = i-1

        # 合并两个排好序的"子串"
        while j >= 0 and i <= len(A)-1:
            sqi = A[i] * A[i]
            sqj = A[j] * A[j]
            if sqi > sqj:
                res.append(sqj)
                j -= 1
            else:
                res.append(sqi)
                i += 1

        # 处理较长的“子串”
        while j >= 0:
            res.append(A[j]*A[j])
            j -= 1
        while i <= len(A)-1:
            res.append(A[i]*A[i])
            i += 1

        return res

---

Subarray Product less than K

这道题是我当前遇到过的最难的题。看了解答后，认为官方解答的思想十分新颖（如果完全让自己想出来十分困难，或许是自己还没开始接触滑动窗口类型的题，不熟练）。核心思想也是双指针/窗口滑动类型：先将双指针的起始位置均放在列表左侧，右指针优先移动。移动时，先用定义的乘积乘以nums[right]，判断是否超过K。若乘积 > K，便用乘积除以nums[left]，并右移左指针，直到乘积小于K为止。之后对左右指针之间满足条件的子集进行计数（恰好为right-left+1）：

class Solution:
    def numSubarrayProductLessThanK(self, nums: list, k: int) -> int:
        # 双指针/滑动窗口思想。
        # 指针利用：先将双指针的起始位置均放在列表左侧，右指针优先移动。先用乘积乘以当前右指针对应的数字，同时判断乘积是否大于k。
        # 若大于，则乘积除以左指针对应数字，并左指针右移，直到乘积小于k为止。之后对当前左右指针之间的元素进行计数（right-left+1）
        # （乘积小于k的连续子数组的个数）

        # 边界条件
        if k <= 1:
            return 0
        res = 0
        left = 0
        product = 1
        for right in range(len(nums)):
            product *= nums[right]

            # 判断当前乘积是否超过K
            while product >= k and left < right:
                product /= nums[left]
                left += 1

            # 对符合条件的子集进行计数
            res += right-left+1

        return res

---

总结

在做了一定数量的双指针题型之后，我发现了一定的规律。虽然每道题都有自己的特征，无法套用同一个模式去解决，但它们之间确实存在一些共性：

1. 大多都是以数组/列表、链表为背景；
2. 题目无要求或未排序情况下，倾向于优先进行排序处理；
3. 结果往往是满足条件的子集或子集的数量
4. 能降低复杂度

如果笔记存在一些问题，发现后我会尽快纠正。

*注：以上题目均来源于leetcode