普利姆算法和克鲁斯卡尔算法求解最小生成树

 Q：最小生成树有什么用？

  A：譬如我要去五个城市旅游，每两个城市之间可能有路也可能没有，路的距离可能一样也可能不一样，随机从一个城市出发，我想要把每个城市走一遍，怎么样走过的路距离最短，比如我想从上海出发，要走遍其他城市，要怎样确定一条路径最短，这就是最小生成树的作用。

求解最小生成树有两种基础算法：普利姆算法和克鲁斯卡尔算法。 

Q:  如何保证最小生成树唯一？

A： 所有边的权值均不相等则构成的最小生成树一定唯一，或者有权值相等的边，但权值相同的边都加入到最小生成树中，这样的最小生成树也唯一。

1.普利姆算法

1.1算法思想：

       从图中任意取出一个顶点为起点，它可以视为一颗树，然后在与该树相邻的边中选取一条权值最小的边，将该边与其对应的顶点也加入到树种，以此类推，最终将所有顶点都加入到树中，这颗树就是最小生成树。一般而言，n个顶点需要执行n-1次构造过程，也就是找n-1条边。

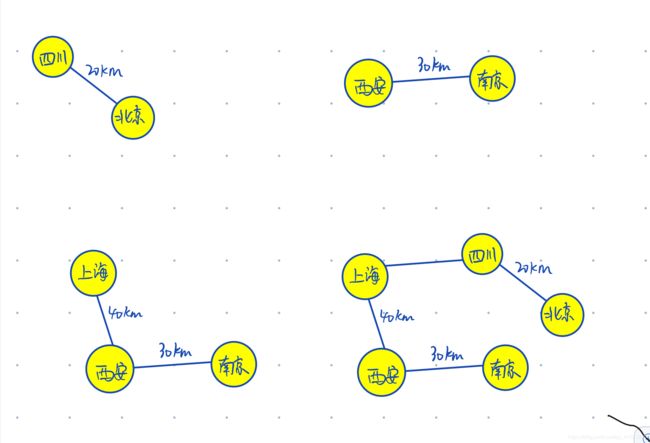
1.2实例分析过程

1.3代码实现： 

#include 
#define MaxVertexNum 100
/* 最大顶点数设为100 */
#define MaxCost 9999
/* 边的权值最大为9999 */
typedef char VertexType;
/* 顶点类型设为字符型 */
typedef int  EdgeType;
/* 边的权值设为整型 */
typedef struct
   { VertexType vexs[MaxVertexNum];
       /* 存放顶点信息 */
      EdgeType  edges[MaxVertexNum][MaxVertexNum];
/* 存放邻接关系 */
      int  n,e; /*顶点数和边数*/
}Mgraph;
void CreateMGraph(Mgraph *G)
  {int i,j,k,w;
    printf("请输入顶点数和边数(输入格式为:顶点数,边数):\n") ;
    scanf("%d,%d",&(G->n),&(G->e));
    printf("请输入顶点信息:\n");
    for(i=0;in;i++) 
        scanf("\n%c",&(G->vexs[i]));
	for(i=0;in;i++)
        for(j=0;jn;j++) 
            G->edges[i][j]=MaxCost;
    printf("请输入每条边对应的两个顶点的序号(输入格式为:i,j,w):\n");
              for(k=0;ke;k++) 
                   { scanf("%d,%d,%d",&i,&j,&w);
                         G->edges[i][j]=w; 
						 G->edges[j][i]=w;  }
    }
void Prim(int gm[][MaxVertexNum],int tree[],int cost[],int n)
  { int i,j,k,mincost,flag[MaxVertexNum];
    for (i=1; i

1.4普利姆算法时间复杂度度：

      时间复杂度为O(n²)，仅与图中顶点有关系，与边数无关，故普利姆算法适合用于稠密图。

     

2.克鲁斯卡尔算法

2.1 克鲁斯卡尔算法思想：

    将图中所有边按照权值大小从小到大排序，然后从最小边开始扫描各边，并检测当前变是否为候选边（该边加入后是否会构成回路），若不构成回路则加入树中，直至所有边都检测完毕。

2.2实例分析过程

 

2.3 代码实现

#include 
#define MaxVertexNum 100
/* 最大顶点数设为100 */
#define MaxEdgeNum 100
/* 最大边数设为100 */
#define MaxCost 9999
/* 边的权值最大为9999 */
typedef char VertexType;
/* 顶点类型设为字符型 */
typedef int  EdgeCost;
/* 边的权值设为整型 */
typedef struct
   { VertexType vexs[MaxVertexNum];
       /* 存放顶点信息 */
      EdgeCost  edges[MaxVertexNum][MaxVertexNum];
/* 存放邻接关系 */
      int  n,e; /*顶点数和边数*/
}Mgraph;
typedef struct
   { int v1;
     int v2;
	 EdgeCost cost;
}EdgeType;
void CreateMGraph(Mgraph *G)
  {int i,j,k,w;
    printf("请输入顶点数和边数(输入格式为:顶点数,边数):\n") ;
    scanf("%d,%d",&(G->n),&(G->e));
    printf("请输入顶点信息:\n");
    for(i=0;in;i++) 
        scanf("\n%c",&(G->vexs[i]));
	for(i=0;in;i++)
        for(j=0;jn;j++) 
            G->edges[i][j]=MaxCost;
    printf("请输入每条边对应的两个顶点的序号(输入格式为:i,j,w):\n");
              for(k=0;ke;k++) 
                   { scanf("%d,%d,%d",&i,&j,&w);
                         G->edges[i][j]=w; 
						 G->edges[j][i]=w;  }
    }
void Sort(Mgraph *G, EdgeType e[],int *EdgeNum)  /* 用Kruskal方法求最小生成树  */ 
  {EdgeType e1;
   int i,j,k,m;
   int mincost;
    m=-1;
    for(i=0;in;i++)
    for(j=i+1;jn;j++)
     if(G->edges[i][j]!=MaxCost)
       {m++;
	    e[m].v1=i;
	    e[m].v2=j;
	    e[m].cost=G->edges[i][j]; 
       }  /*将边存入数组e中*/
   for(i=0;i=0)
      t=father[t];
    return(t);
  }
void Kruskal(EdgeType edges[],EdgeType T[],int m,int n)
/* 假定edges[]中的数据已按cost值由小到大排序 */
 { int father[MaxVertexNum];
   int i,j,vf1,vf2;
   for(i=0;i

 2.4 克鲁斯卡尔时间复杂度分析

     克鲁斯卡尔算法的时间复杂度主要由排序算法来决定，排序算法处理数据的规模由图的边数e决定，与顶点树无关，因此克鲁斯卡尔适合用于稀疏图。

ps：普利姆算法与克鲁斯卡尔算法均是针对无向图的。