动态规划求解-将字符串A变换为字符串B 所用的最少字符操作次数

问题描述：
设A 和B 是2 个字符串。要用最少的字符操作将字符串A 转换为字符串B。
这里所说的字符操作包括
(1)删除一个字符；
(2)插入一个字符；
(3)将一个字符改为另一个字符。
将字符串A变换为字符串B 所用的最少字符操作次数也称为字符串A到B 的编辑距离，记为 d(A,B)。
试设计一个有效算法，对任给的2 个字符串A和B，计算出它们的编辑距离d(A,B)。

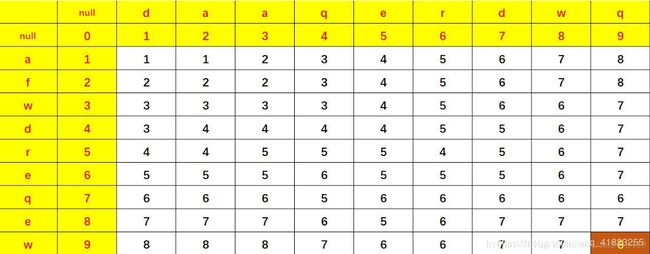
这里抄袭了一位大佬的利用二维数组求解的思路图，做的挺好，他的算法结果也是对的，就给大家摘抄下来了。图片的原博客链接是：https://blog.csdn.net/ma2413419/article/details/82693319#commentsedit。
而很多其他大佬的对于本题求解的算法，其实是有毛病的，就是没考虑到两个字符串第一个元素是否相等的问题，这样的结果会对后面的造成影响。这就叫做一步错，步步错。
好啦，接下来就开始一起看思路与代码吧！
根据变化编辑距离的变化规律，不难得出如下的结论：

 d[i][j]=min(min(d[i-1][j]+1,d[i][j-1]+1),(a[j-1]==b[i-1]?d[i-1][j-1]:d[i-1][j-1]+1));

下面我讲解三种求解该问题的方法：

一、（1）利用二维静态数组求法(c++版)：
顾名思义，就是构造数组取存储每一个对应的字符串a的前i个元素与字符串b的前j个元素的最小编辑距离d[i][j].

#include
#include
int GetMinEditDistance(std::string a,std::string b);
int main()//这种方法有一个不足就是不能返回多个值。如果以指针形式返回，那么就可以得出想要的结果。 
{
	std::string a,b;
	std::cin>>a>>b;
	GetMinEditDistance(a,b);
    std::cout<<GetMinEditDistance(a,b);
	return 0;
 } 
 int GetMinEditDistance(std::string a,std::string b)
 {
 	int length_a=a.length();
 	int length_b=b.length();
 	int d[length_b+1][length_a+1]={0};
 	
	 for(int i=1;i<=length_a;i++)
	 {
	 	d[0][i]=i;    //把第一行行值确定
	 }
 	for(int i=1;i<=length_b;i++)
	 {
	 	d[i][0]=i;    //把第一列列值确定
	 }
 	for(int i=1;i<=length_b;i++)
 	{
 		for(int j=1;j<=length_a;j++)
 		{
 			d[i][j]=std::min(std::min(d[i][j-1]+1,d[i-1][j]+1),a[j-1]==b[i-1]?d[i-1][j-1]:d[i-1][j-1]+1);     //动态求解三种方式下的字符串a的前i个元素与字符串b的前j个元素的最小编辑距离
		 }
	 }
	return d[length_b][length_a];  //返回最小编辑距离数值
 }
 

（2）利用二维静态数组求法(C语言版)：

#include
#include
int editdistance(char a[],int length_a,char b[],int length_b);
 int GetMinNum(int a, int b, int c);
int main()
{
	char a[100];
	char b[100];
	gets(a);
	gets(b);
	int length_a=strlen(a);
	int length_b=strlen(b);
	int c=editdistance(a,length_a,b,length_b);
	
	printf("%d",c);
	return 0;
 } 
 int GetMinNum(int a, int b, int c)//获取三个数中最小数
{
    int min = a < b ? a : b;
    return min < c ? min : c;
}
 
 int editdistance(char a[],int length_a,char b[],int length_b)
 {
 	int d[length_b+1][length_a+1]={0};
 	for(int i=1;i<=length_a;i++)
 	{
 		d[0][i]=i;
	 }
 	for(int i=1;i<=length_b;i++)
 	{
 		d[i][0]=i;
	 }
 	for(int i=1;i<=length_b;i++)
 	{
 		for(int j=1;j<=length_a;j++)
 		d[i][j]=GetMinNum(d[i][j-1]+1,d[i-1][j]+1,b[i-1]==a[j-1]?d[i-1][j-1]:d[i-1][j-1]+1);
	 }
	 return d[length_b][length_a];
 }

二、利用指针法求解（C++版）
要定义指针变量求解的话，必须要首先分配内存空间，让指针指向这一部分内存空间。
对于同一本题，我们需要定义一个指向指针（假设定义为 int *a）的指针变量(那么这个指针变量就可以定义为int * *a)。利用指针法求解的好处是可以通过在定义的函数中返回一个指针值，通过返回到主函数的这个指针值，可以把整个二维数组打印出来。

（1）利用int *p=new int[n]分配内存空间方法求解问题的代码如下：

#include
#include
int** MinEditDistance(std::string a,int length_a,std::string b,int length_b);
int main()
{
	std::string a,b;
	std::cin>>a>>b;
	int length_a=a.length();
 	int length_b=b.length();
	int** p=MinEditDistance(a,length_a,b,length_b);
		for(int i=1;i<=length_b;i++)
 	{
 		for(int j=1;j<=length_a;j++)
    	std::cout<<p[i][j]<<" ";
        std::cout<<std::endl;
	}
	return 0;
 } 
 int** MinEditDistance(std::string a,int length_a,std::string b,int length_b)
 {
 	int **d=new int*[length_b+1];
 	for(int i=0;i<=length_b;i++)
 	{
 		d[i]=new int[length_a+1];
	 }
 	d[0][0]=0;
 	for(int i=1;i<=length_a;i++)
 	{
 		d[0][i]=i;
	 }
 	for(int i=1;i<=length_b;i++)
 	{
 		d[i][0]=i;
	 }
 	for(int i=1;i<=length_b;i++)
 	{
 		for(int j=1;j<=length_a;j++)
 		d[i][j]=std::min(std::min(d[i][j-1]+1,d[i-1][j]+1),a[j-1]==b[i-1]?d[i-1][j-1]:d[i-1][j-1]+1);
	 }
	 return d;
 }

（2）利用int *p=(int *)molloc(sizeof(int))分配内存空间方法求解问题的代码如下:

#include
#include
#include
 int **EditDistance(std::string a,int length_a,std::string b,int length_b);
 int main()
 {
    std::string a,b;
 	std::cin>>a>>b;
 	int length_a=a.length();
 	int length_b=b.length();
 	int **p=EditDistance(a,length_a,b,length_b);
 	for(int i=1;i<=length_b;i++)
 	{
 		for(int j=1;j<=length_a;j++)
 		std::cout<<p[i][j]<<" ";
 		std::cout<<std::endl;
	 }
	 std::cout<<"min="<<p[length_b][length_a];
 	return 0;
  } 
  int **EditDistance(std::string a,int length_a,std::string b,int length_b)
  {
  	int **d=(int **)malloc(length_b*sizeof(int*));
  	for(int i=0;i<=length_b;i++)
  	{
  		d[i]=(int *)malloc(length_a*sizeof(int));
	  }
	  d[0][0]=0;
  	for(int i=1;i<=length_a;i++)
  	{
  		d[0][i]=i;
	  }
	 for(int i=1;i<=length_b;i++)
	  {
	  	d[i][0]=i;
	  }
	  for(int i=1;i<=length_b;i++)
	  {
	  	for(int j=1;j<=length_a;j++)
	  	{
	  		d[i][j]=std::min(std::min(d[i][j-1]+1,d[i-1][j]+1),a[j-1]==b[i-1]?d[i-1][j-1]:d[i-1][j-1]+1);
		  }
	  }
	  return d;
  }

好啦，大概就是这些了，如果再想到啥好的算法，还会和继续和大家分享的，咱们一起讨论，一起进步，希望学习C++/C的广大码农们，一定要坚持哦,加油!