机器学习“傻瓜式”理解（15）SVM（2）

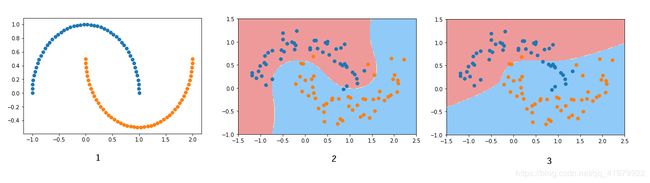
SVM中的非线性数据进行分类

实际的生产活动中我们遇到的数据大多数不能进行严格的区分的，为了解决这种问题，目前为止我们可以通过两种方式来解决：
①直接利用多项式项进行解决。
②利用内核函数（scikit已经封装好的）
下面我们将通过代码的方式进行验证。

1.添加多项式项

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import Standardscaler,PolynomialFeatures
from sklearn.svm import linearSVC
from sklearn.pipeline import Pipeline

'''决策边界'''
from myML.metrics import plot_decision_boundary

'''模拟数据集'''
X,y = datasets.make_moons(noise=0.15,random_state = 666)
'''查看数据集'''
plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()


'''1.使用添加多项式方法'''
def Poly(degree,C= 1.0):
    return Pipeline([
        ('poly',PolynomialFeatures(degree=degree)),
        ('std',Standardscaler()),
        ('svm',linearSVC(C = C))
    ])

poly_svc = Poly(degree=3)
poly_svc.fit(X,y)
plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()


'''2.利用内核函数，直接使用多项式特征'''
from sklearn.svm import SVC
def PolynomialKernelSVC(degree, C=1.0):
    return Pipeline([
        ('std_scaler', StandardScaler()),
        ('kernelSVC', SVC(kernel='poly', degree=degree, C=C))
    ])

poly_kernel_svc = PolynomialKernelSVC(degree=3)
poly_kernel_svc.fit(X, y)

plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

依次运行结果为：

核函数的介绍应用

核函数分为多项式核函数以及线性核函数

多项式核函数的内部实现原理：
首先对传入的数据添加多项式项，然后再返回数据之间进行点乘的结果，其目的便是通过对数据的升维处理使得原本线性不可分的数据线性可分。
例如下例：

转换后：

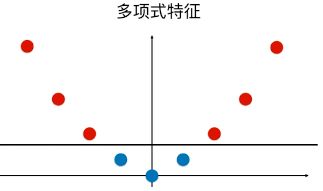
（注意：核函数这种技巧并不是SVM所特有，只要是为了减少计算量或者提高运行速度，都可以使用核函数，但是相对于传统的机器学习算法，核函数这类的技巧更多的是在SVM中使用。）

SVM的核函数
SVM核函数包括两种形式，分别为：
①SVC(kernel = ‘ploy’)：表示算法使用多项式核函数；
②SVC(kernel = ‘rbf’)：表示算法使用高斯核函数；
高斯核函数是找到更有利于分类任务的样本空间，开销巨大，适用于数据集（m,n）m

SVM解决回归问题
回归问题的本质便是找到一条直线，使得其可以最大程度的拟合住样本点，但是SVM的回归问题便是使得在margin区域中的点尽可能的多，然后中间的那条线便是我们想要的模型。