【实例分割论文】SOLO v2: Dynamic, Faster and Stronger

论文名称：《SOLOv2: Dynamic, Faster and Stronger》

论文链接：https://arxiv.org/abs/2003.10152

参考代码：http://github.com/WXinlong/SOLO （v1已开源~）

目录

综述

SOLO v1回顾

整体思路

操作流程（附源代码）

改进空间

SOLO v2

mask learning

Mask kernel branch

Mask feature branch

其他

mask NMS

实验结果

总结

---

综述

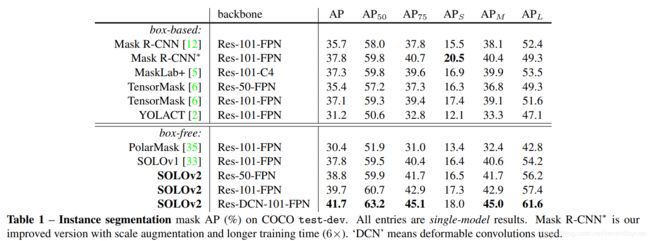
SOLO v2遵循了SOLO的优雅、简单的设计，并且针对mask的检测效果和运行效率做了两个改进：（1）mask learning：能够更好地学习到mask（2）mask NMS：提出了matrix nms，大大减少了前向推理的时间。 最终，SOLOv2相比SOLOv1，AP提升1.9%的同时速度快了33%，light-weight 版本的SOLVv2能够在COCO上达到31.3FPS，37.1%AP。除此之外，SOLO v2还在目标检测和全景分割任务中表现上佳，证实了SOLO的思路有用在更多视觉任务的潜力。

COCO 性能指标

 

SOLO v1回顾

整体思路

SOLO v1 结构图

SOLO的核心思想是：将分割问题转化为位置分类问题，从而做到不需要anchor，不需要normalization，不需要bounding box detections的实例分割。具体做法是：将图片划分成S×S的网格，如果物体的中心（质心）落在了某个网格中，那么该网格就有了两个任务：（1）Category Branch 负责预测该物体语义类别（2）Mask Branch 负责预测该物体的instance mask。这就对应了网络的两个分支。同时，SOLO在骨干网络后面使用了FPN，用来应对尺寸。FPN的每一层后都接上述两个并行的分支，进行类别和位置的预测，每个分支的网格数目也相应不同，小的实例对应更多的的网格。

Category Branch负责预测物体的语义类别，每个网格预测类别S×S×C，这部分跟YOLO是类似的。

重点看一下Mask Branch，每个正样本（有类别输出的网格）都会输出对应类别的instance mask，这里的通道channel和网格的对应关系是：第k个通道负责预测出第（i，j）个网格的instance mask，k = i*S+j。因此输出维度是H×W×(S^2) 。这样的话就有了一一对应的语义类别和class-agnostic的instance mask。

操作流程（附源代码）

SOLO的两个分支光看论文可能会比较迷糊，还好作者昨天开源了源代码，通过代码可以更加清晰地了解head部分的操作流程。总结如下：

（1）首先经过backbone网络和FPN，得到不同层级的图像特征；

（2）对于Category分支，首先将FPN最高层的特征从H×W×256对齐至S×S×256（256为特征通道数），然后经过一系列卷积（7个3×3卷积）提取特征，最后再经过一个3×3卷积将输出对齐到S×S×C（C为预测类别-1）；

# cate branch
for i, cate_layer in enumerate(self.cate_convs):
    if i == self.cate_down_pos:
        seg_num_grid = self.seg_num_grids[idx]
        cate_feat = F.interpolate(cate_feat, size=seg_num_grid, mode='bilinear')
        # 将FPN最高层的特征从H*W*feat_channel 对齐到 S*S*feat_channel
    cate_feat = cate_layer(cate_feat) # 7个卷积 
cate_pred = self.solo_cate(cate_feat) # 从 S*S*feat_channel 到 S*S*num_classes

（3）对于Mask分支，首先对FPN最高层的特征做一个CoordConv，然后同样经过一系列卷积（7个3×3卷积）提取特征，此时维度为H×W×256，再做一步上采样至2H×2W×256，最后就是对齐到2H×2W×S^2的输出（Decoupled SOLO此处则为2H×2W×S）

# ins branch
# concat coord
x_range = torch.linspace(-1, 1, ins_feat.shape[-1], device=ins_feat.device)
y_range = torch.linspace(-1, 1, ins_feat.shape[-2], device=ins_feat.device)
y, x = torch.meshgrid(y_range, x_range)
y = y.expand([ins_feat.shape[0], 1, -1, -1])
x = x.expand([ins_feat.shape[0], 1, -1, -1])
coord_feat = torch.cat([x, y], 1)
ins_feat = torch.cat([ins_feat, coord_feat], 1) # CoordConv

for i, ins_layer in enumerate(self.ins_convs): # 7个3*3 Conv 提取特征
    ins_feat = ins_layer(ins_feat)  # H*W*feat_channel

ins_feat = F.interpolate(ins_feat, scale_factor=2, mode='bilinear') # 上采样到2H*2W*feat_channel
ins_pred = self.solo_ins_list[idx](ins_feat) 
# 从2H*2W*feat_channel到2H*2W*(S^2) S^2的复杂度，这里也是Decoupled 和 Solo v2的优化之处

改进空间

不同的mask head对比

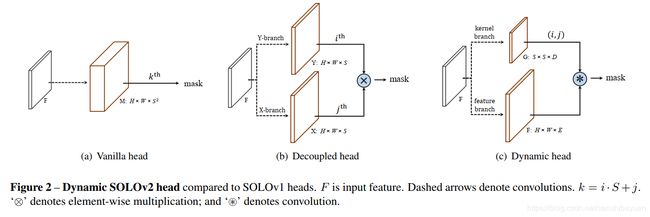
仔细来看一下mask branch的最后一层的情况，如图中的（a）所示：这其实是一个1×1的卷积，以特征F（维度为H×W×E）做输入，输出M（维度为H×W×(S^2)），S^2的输出通道。这里卷积核设为G，G的维度就是1×1×E×(S^2)。这一层的操作其实是M=F∗G，作用是生成S×S个分类器，每个分类器都用来判断像素点是否属于这个位置的类别。

在SOLO v1中也提到了，包含S×S输出通道的M是冗余的，因为在大多数情况下物体在图片中的分布都是稀疏的，起到作用的通道（分类器数目）远远少于S×S。因此SOLO v1提出了Decoupled SOLO，如图中的（b）所示，通过将这些分类器分解成X和Y两个方向，将输出通道从S×S降到了S+S。

SOLO v2中提出了另一种思路，更加直接，如图中的（c）所示。由于M=F∗G中的M是冗余，F是固定的，那么就可以直接去学习卷积核G。这样做的话有三个好处：

1. 可以直接从S×S的分类器中挑选出有效（valid）的部分作为结果，减少了模型参数；
2. 卷积核的参数是基于输入预测的，更加flexible and adaptive；
3. 最终得到的S×S的分类器是基于location的，这跟SOLO的本质思想（segmenting objects by locations）是相符合的，并且将其延伸到了predicting the segmenters by locations这一新高度。

此外，由于SOLO是一个完全box-free的算法，没有依赖box去生成mask，因此不需要做box的NMS，但取而代之的是需要做mask的NMS，但mask NMS是一个比较费时间的地方，复杂度比box NMS高不少，这也是SOLO需要优化的点。

P.S：关于SOLO的详情解读可以看我之前的论文笔记：

【实例分割论文】 SOLO：Segmenting Objects by Locations

关于其他单阶段实例分割方法如YOLACT和BlendMask可以看我的另一篇文章：

【进展综述】单阶段实例分割（Single Shot Instance Segmentation）

SOLO v2

mask learning

使用dynamic head的mask branch

SOLO v2中的mask branch 被分解为mask kernel branch和mask feature branch，分别对应卷积核的学习和特征的学习。两个分支的输出最终组合成整个mask branch的输出。

Mask kernel branch

Mask kernel branch用来学习卷积核，即分类器的权重，有点类似STN和Dynamic Filter的思路。这里输入为H×W×E的特征F，其中E是输入特征的通道数；输出为卷积核S×S×D，其中S是划分的网格数目，D是卷积核的通道数。对应关系如下：1×1×E的卷积核，则D=E，3×3×E的卷积核，则D=9E，以此类推。注意到这里不需要激活函数。

Mask feature branch

Mask feature branch用来学习特征的表达，它的输入是backbone+FPN提取的不同层级的特征，输出是H×W×E的mask feature，用F表示。SOLO框架中一个重要的设计就是采用了FPN，应对不同的尺寸。如何将不同层级的特征融合得到mask feature是一个重要的部分。通常来说，可以有两种做法：

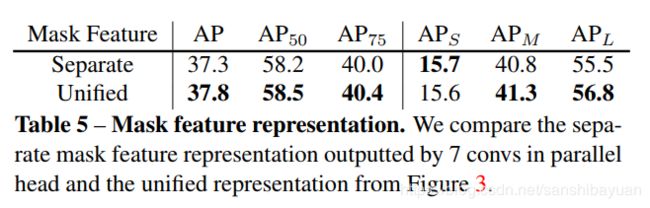
1. unified maskfeature representation：对每一层级都预测一个mask feature，再进行融合（predict the maskfeatures for each FPN levels）
2. separate maskfeature representation：直接对所有的层级预测一个统一的mask feature（predict a unified maskfeature representation for all FPN levels）。

不同mask feature表达的对比实验

unified maskfeature representation

经过试验对比，作者选择了unified maskfeature representation。具体的实现则参考了Panotic FPN中的feature pyramid fusion，将FPN的P2到P5层分别依次通过【若干个3×3卷积 + group norm + ReLU + 2个双线性插值操作】，统一到原图的1/4尺寸，再做element-wise summation，最后接【1 × 1 convolution + group norm + ReLU】。

需要注意的是这里的 CoordConv 是在FPN的最高层（原图的1/32尺寸）使用，位置在3×3卷积和双线性插值之前。CoordConv的作用与SOLO v1中相同，提供更准确的位置敏感信息和实例特征信息。

其他

有了前两个分支的输出，生成mask也就水到渠成。具体的做法是：对于在(i,j)的每个网格，先获得卷积核G，然后将其与特征F卷积得到实例Mask，这会生成【最多】S×S个mask。最后，使用Matrix NMS方法得到最终的实例分割结果。

损失函数和标签分配方法等与SOLO v1保持一致。

在前向预测的过程中，图像先通过backbone和FPN，得到grid(i,j)位置的类别分值P(i,j)之后，先用较低的置信度阈值0.1筛选一遍结果后，再进行卷积提取mask 特征。mask特征与预测得到的卷积核进行卷积，再经过一个sigmoid操作，然后用0.5的阈值生成binary mask，最后做一步Matrix NMS，得到结果。

mask NMS

NMS是视觉任务的老熟人了，其缺点是繁琐、冗余的计算，此外，mask NMS 会比bbox NMS 造成更多的计算时间。对NMS的优化已经有了不少工作，通常分为两类，一是Soft NMS和Adaptive NMS，主要优化了精度；另一类是YOLACT中的Fast NMS，主要优化了速度。

SOLO v2中提出了Matrix NMS，思路源于Soft NMS，效果类似Fast NMS。使用并行的矩阵运算单次地实现NMS，Matrix NMS可以做到在不到1ms的时间里处理500张mask，并且比目前最快的Faster NMS要高0.4% AP。

Soft NMS的思路通过递归地根据IoU降低其他bbox的检测分数，分数较高的检测结果被降低分数后将被以很小的阈值消除。经过优化，这种顺序的过程与传统的Greedy NMS一样是顺序的，无法并行实现。

Matrix NMS的思路是

对于一个预测得到的mask，它的decay factor主要受两部分影响：

一是得分大于j点的所有i点对i的惩罚，这个很好实现，直接通过算一个包含IoU的衰减函数（线性衰减或高斯衰减）就能得到；

二是整个mask被抑制的概率，这个概率就比较难直接算，但它通常与IoU有着正相关的关系。因此，Matrix NMS提出直接将最大重复的预测结果（对应最大的IoU值）的结果来近似这个抑制概率

最后得到的decay factor就是，预测的分值就通过这个decay factor单步更新

Matrix NMS实现可以一次性完成，不需要循环重复，具体的实现就不多说了，附上伪代码和对比实验结果。

Matrix NMS的Python伪代码

Matrix NMS的对比实验

实验结果

实验结果就没啥好说的了，总的来说：更快更强，适应不同任务/不同数据集；分割效果来说，也要更加精细。

COCO instance segmentation

COCO object detection

与Mask R-CNN对比

总结

延续了SOLO的良好思路，改进点也很扎实，期待继续出v3~