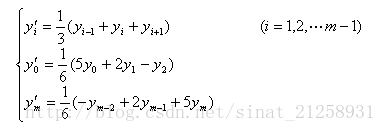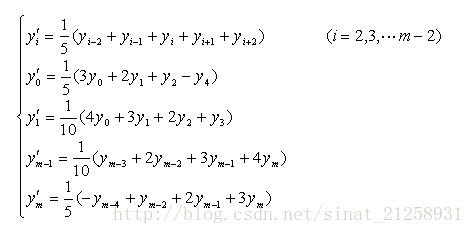Savitzky-Golay平滑滤波的python实现

Savitzky-Golay平滑滤波是光谱预处理中常用滤波方法，它的核心思想是对一定长度窗口内的数据点进行k阶多项式拟合，从而得到拟合后的结果。对它进行离散化处理后后，Ｓ-Ｇ 滤波其实是一种移动窗口的加权平均算法，但是其加权系数不是简单的常数窗口，而是通过在滑动窗口内对给定高阶多项式的最小二乘拟合得出。

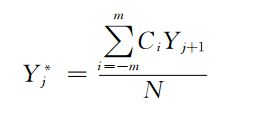
接下来以二阶多项式情况下的直线滑动平均法作为特殊例子，进行详细分析，并给出通用的多阶加权系数计算方法以及python实现的代码。
文章结构：

---

直线滑动平均法

对自变量x按等距△x作实验观测得数据如下:

令 t=x−xiΔx t = x − x i Δ x ，上述数据变为

用下面的方法 yi y i 修正的值:取定正整数n，使 i−n>=0和i+n<=m i − n >= 0 和 i + n <= m 至少有一个成立。

• 当 i−n>=0和i+n<=m i − n >= 0 和 i + n <= m 同时成立，及窗口不在数据边缘时，选取 ai和bi a i 和 b i 使得
  
  解得：
  
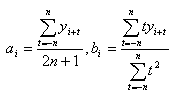
  于是得 t=i−n,i−n+1,...,i,i+1,...,i+n t = i − n , i − n + 1 , . . . , i , i + 1 , . . . , i + n 时的修正公式:
  
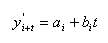
  假设当t = 0, 可得修正值：
  
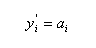
• 当 i−n>=0和i+n<=m i − n >= 0 和 i + n <= m 只有一个成立，既窗口在数据边缘时，这里不做特别讨论，在实现时的思路是将数据按照首尾的值进行拓展，当然这个思路不够严谨，读者如果希望更为可靠可以自行研究这一部分。
• 由此，可以得到直线滑动平均法在窗口大小为3点，5点，7点…时的结果分别为
  
  • 3点
    
  • 5点
    

---

通用的多阶加权系数计算方法

通过以上二阶多项式拟合的例子分析，我们可以对S-G方法有个形象的认识。接下来给出通用的多阶加权系数计算方法。

• 设滤波窗口的宽度为 n=2m+1 n = 2 m + 1 ，各测量点为 x=（−m,−m+1,0,,,,0,1,…m−1,m） x = （ − m , − m + 1 , 0 , , , , 0 , 1 , … m − 1 , m ） 采用 k−1 k − 1 次多项式对窗口内的数据点进行拟合
  
• 于是就有了n个这样的方程，扣成了k元线性方程组。要使方程组有解则n应大于等于k，一般选择n>k，通过最小二乘法拟合确定拟合参数A。由此得到
  
  其中， B=X∗(XT∗X)−1∗XT B = X ∗ ( X T ∗ X ) − 1 ∗ X T .
  由此可得，修正值 yi′=Y′i y i ′ = Y ′ i
• 此处同样不考虑窗口在数据边缘时的加权系数计算，实现时处理思路同上。

---

python实现

# -*- coding: utf-8 -*-  
import numpy as np

"""
* 创建系数矩阵X
* size - 2×size+1 = window_size
* rank - 拟合多项式阶次
* x - 创建的系数矩阵
"""
def create_x(size, rank):
    x = []
    for i in range(2 * size + 1):
        m = i - size
        row = [m**j for j in range(rank)]
        x.append(row) 
    x = np.mat(x)
    return x

"""
 * Savitzky-Golay平滑滤波函数
 * data - list格式的1×n纬数据
 * window_size - 拟合的窗口大小
 * rank - 拟合多项式阶次
 * ndata - 修正后的值
"""
def savgol(data, window_size, rank):
    m = (window_size - 1) / 2
    odata = data[:]
    # 处理边缘数据，首尾增加m个首尾项
    for i in range(m):
        odata.insert(0,odata[0])
        odata.insert(len(odata),odata[len(odata)-1])
    # 创建X矩阵
    x = create_x(m, rank)
    # 计算加权系数矩阵B
    b = (x * (x.T * x).I) * x.T
    a0 = b[m]
    a0 = a0.T
    # 计算平滑修正后的值
    ndata = []
    for i in range(len(data)):
        y = [odata[i + j] for j in range(window_size)]
        y1 = np.mat(y) * a0
        y1 = float(y1)
        ndata.append(y1)
    return ndata

• 边缘数据处理方法不是十分严谨，如读者有更高的要求可以自行修改。

  实验结果

  对一段实际的光谱数据进行滑动窗口为5，多项式阶数为3的S-G平滑滤波后，得到的结果如下图所示：
  
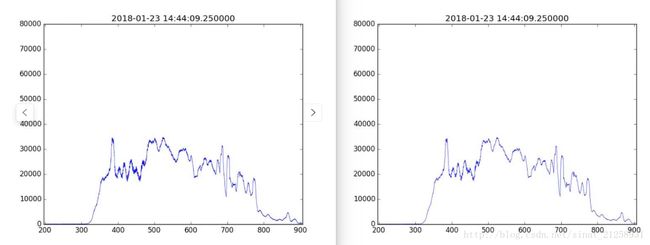
  由于实验数据点数较多，大约为3000多个点，此处实验效果不是非常明显，但是可以看到的是在400-500nm波段，500-600nm波段内数据明显变得更加光滑。

---

本文综合参考了以下文献，在这里致以衷心的感谢：

1. 《Savitzky-Golay平滑去噪》：
   http://blog.csdn.net/qq_20823641/article/details/51537461
2. 黄耀欢, 王建华, 江东, 等. 利用 SG 滤波进行 MODIS-EVI 时间序列数据重构[J]. 武汉大学学报信息科学版, 2009, 34(12): 1440-1443.
3. 毕志伟, 叶鹰. 数学手册:大学生用[M]. 高等教育出版社, 2014.