OpenCV（一）——高斯卷积核原理及代码实现

贴出getGaussianKernel源码

在smooth.cpp中

提示：Gaussian核基于 正态分布函数设计

μ是均值，σ^2是方差

正态函数（即一维Gaussian卷积核）如下

二维卷积核通过对一维积分得到，并且μ = 0

根据如下源码可知：sigma根据如下公式推得,其中ksize是卷积尺寸（方阵长或宽）

sigma = ((ksize-1)*0.5 – 1)*0.3 + 0.8。

但是注意的是该源码是在限制尺寸 1~7，设置sigma = 0就是使用如下代码的默认参数。

static const float small_gaussian_tab[][SMALL_GAUSSIAN_SIZE] =  
	    {  
	        {1.f},  
	        {0.25f, 0.5f, 0.25f},  
	        {0.0625f, 0.25f, 0.375f, 0.25f, 0.0625f},  
	        {0.03125f, 0.109375f, 0.21875f, 0.28125f, 0.21875f, 0.109375f, 0.03125f}
	    }; 

/****************************************************************************************\
                                     Gaussian Blur
\****************************************************************************************/

cv::Mat cv::getGaussianKernel( int n, double sigma, int ktype )
{
	const int SMALL_GAUSSIAN_SIZE = 7;
	static const float small_gaussian_tab[][SMALL_GAUSSIAN_SIZE] =
	{
		{1.f},
		{0.25f, 0.5f, 0.25f},
		{0.0625f, 0.25f, 0.375f, 0.25f, 0.0625f},
		{0.03125f, 0.109375f, 0.21875f, 0.28125f, 0.21875f, 0.109375f, 0.03125f}
	};

	const float* fixed_kernel = n % 2 == 1 && n <= SMALL_GAUSSIAN_SIZE && sigma <= 0 ?
		small_gaussian_tab[n>>1] : 0;

    CV_Assert( ktype == CV_32F || ktype == CV_64F );
    Mat kernel(n, 1, ktype);
    float* cf = kernel.ptr();
    double* cd = kernel.ptr();

    double sigmaX = sigma > 0 ? sigma : ((n-1)*0.5 - 1)*0.3 + 0.8;
    double scale2X = -0.5/(sigmaX*sigmaX);
    double sum = 0;

    int i;
    for( i = 0; i < n; i++ )
    {
        double x = i - (n-1)*0.5;
        double t = fixed_kernel ? (double)fixed_kernel[i] : std::exp(scale2X*x*x);
        if( ktype == CV_32F )
        {
            cf[i] = (float)t;
            sum += cf[i];
        }
        else
        {
            cd[i] = t;
            sum += cd[i];
        }
    }

    sum = 1./sum;
    for( i = 0; i < n; i++ )
    {
        if( ktype == CV_32F )
            cf[i] = (float)(cf[i]*sum);
        else
            cd[i] *= sum;
    }

    return kernel;
}

 贴出代码实现

#include 
using namespace cv;
int main()
{
	Mat g = getGaussianKernel(5, 0);
	g = g * g.t() * 256 ;//g * g的转置得到二维高斯卷积核 (5*1 * 1*5) = (5*5)
	std::cout << g << std::endl;
	system("pause");
    return 0;
}

256是原先归一化的系数的倒数

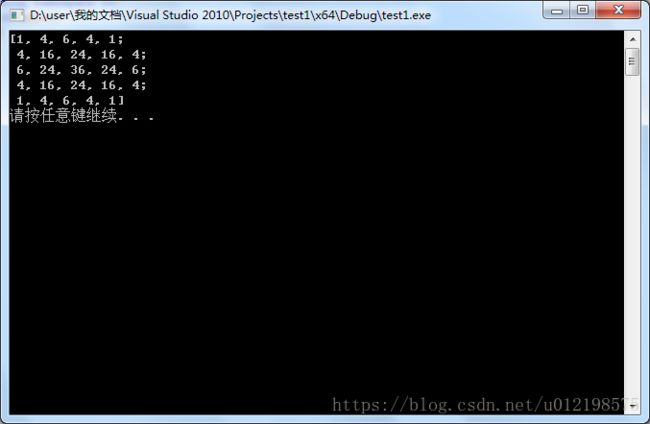
得到结果 

其实限制死的参数 是 真正带入sigma运算结果的近似值，只不过在卷积核小的时候影响不大罢了。

其实高斯卷积核对于视觉领域实在是影响太大了，不得不把源码抠出来深度理解下。不然不知道各个参数是什么意思。对后续opencv知识的学习就更难掌握了。