deeplearning系列（五）实现一个简单的深度神经网络

1. 深度学习概览

在浅层神经网络的介绍中，实现了包含一个隐藏层的浅层神经网络，对于这样的浅层网络，在网络训练过程中可以通过反向传播算法得到较优的网络参数值。然而，因为只有一个隐藏层，限制了模型的表达能力。

在本节中，开始介绍包含多个隐藏层的深度神经网络，经过多个隐藏层对上一层的非线性变换，深度神经网络有远超过浅层网络的表达能力。

但训练深度神经网络并不是一件十分轻松的工作，浅层神经网络的训练经验不能直接移植过来。这其中主要存在一下几方面原因：

1. 数据量大小。浅层神经网络的训练依赖于有标签的数据。深度网络，因其远超过浅层网络的参数量，需要更多的有标签数据来训练，而通常这样的数据是很难获取的。
2. 局部极值。神经网络是一个非凸的优化问题，对于浅层网络来说，可以通过训练使参数收敛到合理的局部极值。而深度网络是一个高度非凸的问题，存在很多的坏的局部极值，使用梯度下降法一般不能收敛到合理的参数值。
3. 梯度弥散。使用反向传播计算梯度时，当网络层次很多时，网络前几层梯度幅值很小。使用梯度下降时，前几层参数更新速度也因此变得缓慢，这些层不能从样本中有效学习。

那么有没有可以解决这些问题的方案，从而使深度网络的训练是可行的呢？采用逐层贪婪训练得到每层参数，然后再使用解决浅层神经网络的算法（例如：BP+L-BFGS）对参数微调是一个比较可行的解决方案。

2. 栈式自编码神经网络

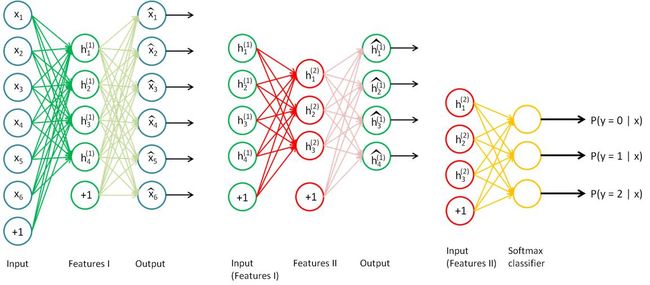
栈式自编码神经网络是一个由多层稀疏自编码器组成的神经网络，前一层自编码器的输出作为后一层的输入。栈式自编码神经网络参数是通过逐层贪婪训练获得的。以一个包含2个隐藏层，输出层为softmax的神经网络为例，其训练过程可以表示为：

1. 用原始输入 x 训练第一个自编码器，学习原始输入的一阶特征 h(1) ，如下图（左）所示；
2. 将所有训练数据输入上面第一个自编码器，得到其一阶特征 h(1) ，然后作为第二个自编码器的输入，学习原始输入的二阶特征 h(2) 如下图（中）所示；
3. 将所有一阶特征输入到训练好的第二个自编码器，得到所有的二阶特征 h(2) ，作为softmax分类器的输入，训练分类器的参数。

3. 参数微调

在上述预训练结束之后，将上面三层结合起来得到包含两个隐藏层和一个softmax输出层的栈式自编码网络，如下图所示。

然后采用反向传播算法调整所有层的参数，这个过程称为微调。微调过程中，网络所有层的全部参数都被优化，经过微调后，可以大幅提高神经网络的分类性能。

4. 代码实现

代码结构为：

• STEP：0-1是参数设置及训练数据的获取部分；
• STEP：2-4是栈式自编码训练部分。包括两个自编码器和一个softmax回归训练部分，经过这样的训练，可以得到一个适合微调的参数初始值；
• STEP：5是参数的微调部分，包括使用反向传播计算梯度和用L-BFGS优化参数。
• STEP：6用经过训练后的网络参数对测试数据集中的数据进行测试。

%% STEP 0: Here we provide the relevant parameters values 
inputSize = 28 * 28;
numClasses = 10;
hiddenSizeL1 = 200;    % Layer 1 Hidden Size
hiddenSizeL2 = 200;    % Layer 2 Hidden Size
sparsityParam = 0.1;   % desired average activation of the hidden units.
lambda = 3e-3;         % weight decay parameter       
beta = 3;              % weight of sparsity penalty term

%% STEP 1: Load data from the MNIST database
trainData = loadMNISTImages('mnist/train-images.idx3-ubyte');
trainLabels = loadMNISTLabels('mnist/train-labels.idx1-ubyte');
trainLabels(trainLabels == 0) = 10; % Remap 0 to 10 since our labels need to start from 1

%% STEP 2: Train the first sparse autoencoder
sae1Theta = initializeParameters(hiddenSizeL1, inputSize);
addpath minFunc/
options.Method = 'lbfgs'; % Here, we use L-BFGS to optimize our cost function. 
options.maxIter = 400;    % Maximum number of iterations of L-BFGS to run 
options.display = 'on';
[sae1OptTheta, cost] = minFunc( @(p) sparseAutoencoderCost(p,inputSize, hiddenSizeL1, 
                                   lambda, sparsityParam,beta, trainData), 
                                   sae1Theta, options);

%% STEP 3: Train the second sparse autoencoder
[sae1Features] = feedForwardAutoencoder(sae1OptTheta, hiddenSizeL1,inputSize, trainData);
sae2Theta = initializeParameters(hiddenSizeL2, hiddenSizeL1);
[sae2OptTheta, cost] = minFunc( @(p) sparseAutoencoderCost(p, ...
                                   hiddenSizeL1, hiddenSizeL2, ...
                                   lambda, sparsityParam, ...
                                   beta, sae1Features), ...
                                   sae2Theta, options);

%% STEP 4: Train the softmax classifier
[sae2Features] = feedForwardAutoencoder(sae2OptTheta, hiddenSizeL2, ...
                                        hiddenSizeL1, sae1Features);
saeSoftmaxTheta = 0.005 * randn(hiddenSizeL2 * numClasses, 1);
softmaxModel = softmaxTrain(hiddenSizeL2, numClasses, lambda, ...
                            sae2Features, trainLabels, options);
saeSoftmaxOptTheta = softmaxModel.optTheta(:);

%% STEP 5: Finetune softmax model
stack = cell(2,1);
stack{1}.w = reshape(sae1OptTheta(1:hiddenSizeL1*inputSize), ...
                     hiddenSizeL1, inputSize);
stack{1}.b = sae1OptTheta(2*hiddenSizeL1*inputSize+1:2*hiddenSizeL1*inputSize+hiddenSizeL1);
stack{2}.w = reshape(sae2OptTheta(1:hiddenSizeL2*hiddenSizeL1), ...
                     hiddenSizeL2, hiddenSizeL1);
stack{2}.b = sae2OptTheta(2*hiddenSizeL2*hiddenSizeL1+1:2*hiddenSizeL2*hiddenSizeL1+hiddenSizeL2);
[stackparams, netconfig] = stack2params(stack);
stackedAETheta = [ saeSoftmaxOptTheta ; stackparams ];
[stackedAEOptTheta, cost] = minFunc( @(p) stackedAECost(p, ...
                                   inputSize, hiddenSizeL2, ...
                                   numClasses,netconfig,lambda, ...
                                   trainData, trainLabels), ...
                                   stackedAETheta, options);

%% STEP 6: Test 
testData = loadMNISTImages('mnist/t10k-images.idx3-ubyte');
testLabels = loadMNISTLabels('mnist/t10k-labels.idx1-ubyte');
testLabels(testLabels == 0) = 10; % Remap 0 to 10
[pred] = stackedAEPredict(stackedAETheta, inputSize, hiddenSizeL2, ...
                          numClasses, netconfig, testData);
acc = mean(testLabels(:) == pred(:));
fprintf('Before Finetuning Test Accuracy: %0.3f%%\n', acc * 100);
[pred] = stackedAEPredict(stackedAEOptTheta, inputSize, hiddenSizeL2, ...
                          numClasses, netconfig, testData);
acc = mean(testLabels(:) == pred(:));
fprintf('After Finetuning Test Accuracy: %0.3f%%\n', acc * 100);

用L-BFGS优化参数，需要提供一个输入是网络参数：theta，输出是网络输出：cost和参数梯度：grad的函数。其中函数梯度是用反向传播算法得到的，代码如下：

function [ cost, grad ] = stackedAECost(theta, inputSize, hiddenSize, ...
                                              numClasses, netconfig, ...
                                              lambda, data, labels)
softmaxTheta = reshape(theta(1:hiddenSize*numClasses), numClasses, hiddenSize);
stack = params2stack(theta(hiddenSize*numClasses+1:end), netconfig);
softmaxThetaGrad = zeros(size(softmaxTheta));
stackgrad = cell(size(stack));
for d = 1:numel(stack)
    stackgrad{d}.w = zeros(size(stack{d}.w));
    stackgrad{d}.b = zeros(size(stack{d}.b));
end
m = size(data, 2);
groundTruth = full(sparse(labels, 1:m, 1));

% Forward propagation
z2 = stack{1}.w*data + repmat(stack{1}.b,1,m);
a2 = sigmoid(z2);
z3 = stack{2}.w*a2 + repmat(stack{2}.b,1,m);
a3 = sigmoid(z3);
z4 = softmaxTheta*a3;
z4 = bsxfun(@minus, z4, max(z4, [], 1));
a4 = exp(z4);
a4 = bsxfun(@rdivide, a4, sum(a4));

% Back propagation
delta4 = -(groundTruth-a4);
delta3 = (softmaxTheta'*delta4).*sigmoidGrad(z3);
delta2 = (stack{2}.w'*delta3).*sigmoidGrad(z2);
softmaxThetaGrad = 1./m *delta4*a3';
stackgrad{2}.w = 1./m *delta3*a2';
stackgrad{2}.b = 1./m *sum(delta3,2);
stackgrad{1}.w = 1./m *delta2*data';
stackgrad{1}.b = 1./m *sum(delta2,2);
softmaxThetaGrad = softmaxThetaGrad+lambda*softmaxTheta;
stackgrad{2}.w = stackgrad{2}.w+lambda*stack{2}.w;
stackgrad{1}.w = stackgrad{1}.w+lambda*stack{1}.w;

% cost calculation
cost = -(1./m)*sum(sum(groundTruth.*log(a4))) + lambda/2.0*sum(sum(theta.^2));

%% Roll gradient vector
grad = [softmaxThetaGrad(:) ; stack2params(stackgrad)];
end

分别使用下面两种参数值对测试数据进行分类：

• 仅使用预训练得到的参数；
• 预训练加微调后的参数；

在测试数据上的分类结果为：

Before Finetuning Test Accuracy: 91.950%
After Finetuning Test Accuracy: 98.280%

可以看出，微调后的结果将分类准确率提高了6.3个百分点。

参考内容：
1. http://ufldl.stanford.edu/wiki/index.php/UFLDL_Tutorial