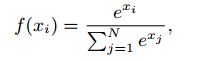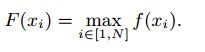论文阅读笔记（一）——Deep Convolutional Neural Network with Independent

摘要：

这篇文章主要是解决 MS-Celeb-1M 的挑战，这一挑战的目的是解决同时识别100K 位明星。为了解决这个问题，提出了一个独立的softmax模型来将单个分类器分成几个小分类器。同时，训练数据分为几个分区。并且介绍了两个模型合并的方法。

 

1.介绍

MS-Celeb-1M 挑战所引发的的问题（1）如何在短时间内区分100k类的数据（2）在训练过程中不包含某些类别会发生什么情况？

同时，第二个问题的直接回答是，模型将返回最相似的类作为结果。

在人脸识别中，这意味着分类器会在所有人的训练中找到最相似的人物。但分类器会有多么自信？

以二进制分类为例，我们怎么知道牵引器样本是否不属于两个类？

答案是我们不能。但是，如果分类器给出了五十五个预测，那么它有一个更大的可能性是比99％概率成为一个类的样本的干扰物。扩展到多类问题，如果分类器给出一个样本的所有预测相同的概率1 / N，其中N是类的数量，则该样本有更大的机会成为干扰物。

这给了我们一个洞察，一个样本的多级分类的最该的概率也可以被看作是这个样本属于这些类的置信度的指标。

概率越高，这个样本越有信心，反之亦然。

在本文中，我们通过引入独立的softmax模型来解决大规模图像分类问题。
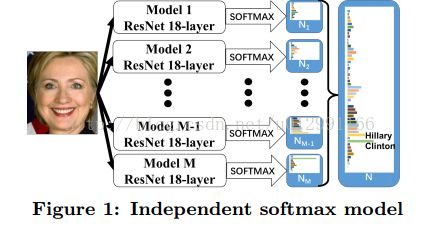
我们不是直接训练一个分类器来同时预测所有的类，而是使用每个softmax函数来训练几个独立的网络，以预测一部分类的概率。通过这样做，大量的类和图像被分成几个小组。每个组的分类问题的规模都会降低，并且可以使用一些很成熟的技术来解决。

 

2.方法

2.1 softmax Model（SM）

          

Xi是第i维的输出，N是维数（等于类别数），f(Xi)视为这一样本属于第i类的概率，则

           

取最大概率的类为该样本所属类别。

样本过大时，SM存在的问题：

（1）首先，最后一层的巨大参数不仅使前向后向传播缓慢，而且在使用多个GPU时也使同步困难。

（2）第二，融合也不能保证。

2.2 Independent Softmax Model（ISM）

为了解决大规模分类问题，提出一个假设，描述如下：

假设：如果一个样本不属于训练类，则具有与softmax模型中的任何类相同的概率。更准确地说，对于不在N类中的样本的i类的预测可以写为

       

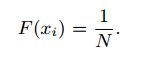
换句话说，对所有类中看不到的类在所有分类器中具有相同的概率。

相反，我们在ISM中使用的这个假设的关键命题是

假设：如果分类器不包含一个类，则该类图像的预测将比包含的分类器得分更低。
在数学上，这可以被形式化为

   

P！=q ，p，q属于[1,M]。

在本文的模型中，N类被分为M个包，第K个包包含Nk个类，即N= N1+……+Nm，则对一个样本的预测可以为：

             

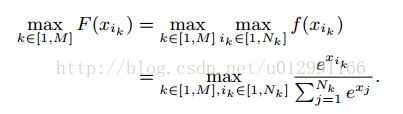
从上可以看出，每个类别的概率先从每一个包中计算，然后再选择可能性最大的作为样本所属的类别。

           

但是，对于每一个包依然是分类的问题。

2.3 融合SM和ISM

为了融合两个模型，我们首先使用非线性的映射函数映射两个评分到相同的规模，映射之后，两个模型可以直接融合。图二：说明了排序后的得分；图三：SM和ISM的得分分别作为X，Y轴，这是用于将由模型SM生成的分数映射到模型ISM的曲线。

          

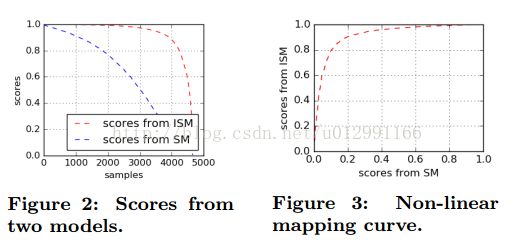
函数tanh和sigmoid首先用于独立拟合该曲线，但显示不良结果。

最后，利用函数tanh和sigmoid形的线性组合。

拟合功能如下

      

S2表示模型A的得分；S12表示映射后的得分，a,b,c,d根据经验为0.3，0.45,0.7,13.44

融合算法如下：

      

3 实验

3.1 数据集和评价指标

    MS-Celeb-1M包含99892类，包含8.46百万图片和50000张图片做测试集，训练集只覆盖75%的类别，

此外，两种不同的数据被用于开发和测试。第一种数据有很大的变化，更难，这被称为dev1。随机选择另一种数据，并且更容易，这被称为dev2。我们以95％和99％的精度评估识别覆盖率，定义为

    

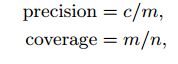
n测试集的个数，c为m个测试数据中正确的个数。

3.2实现细节

    为了训练和验证分类模型，首先将846万张图像随机分为训练集和验证集。

对于每个课程，其90％的图像用于训练，其余10％用于验证。

    

ISM：将数据集分为5个包，拆分细节如下：

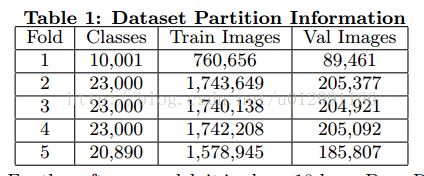
深层剩余网络[18]的18层模型用于每个包的分类。

 

SM：对于softmax模型，它也是在整个数据集上训练的18层深度残差网络模型。它有99,892个输出，每个对应一个类。

 

3.3 实验结果

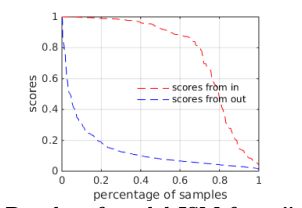
命题的验证：我们从第二个折叠训练的模型验证公式4。

在1k开发图像中，198个图像的类别属于第二个折叠。

在图4中，来自第二模型的这些图像的分数被标记为来自“in”的分数。

其余的802的图像从第二个模型被标记为从“出”的分数。

将样本的百分比作为x轴，得分用作y轴。 从图4可以看出，70％的“in”图像的分数高于0.8。 同时，大约只有1％的“输出”图像得分高于0.8分。

这表明，一个softmax分类器将给予不在其训练集中的类别的图像较低的分数，但是对于该类别的图像给出更高的分数。因此，该命题是合理的。

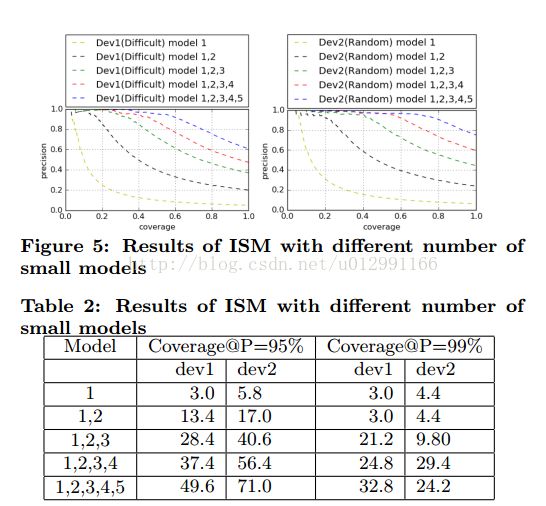
ISM：从图表二：可以看出当有更多的模型加入，我们就可以获得更高的准确率。