浮点数与字节数据转换详解
本文参考网络上的诸多文章,首先分析了单精度浮点数是如何在机器中存储的,然后将浮点数转换为内存中显示的字节数据,进而又将字节数据转换为单精度浮点数。主要用于对数据存储的分析和字节流转换为有效数据方面。
这个知识点是自己本科毕业时候遇到的一个难点,今天终于把它搞明白了。念念不忘,必有回响,加油!
本文主要参考了一下几位博主的文章,非常感谢!
http://blog.csdn.net/gshgsh1228/article/details/51221354
http://blog.csdn.net/rayxp/article/details/40855665
http://www.cnblogs.com/jillzhang/archive/2007/06/24/793901.html
http://www.cnblogs.com/zhugehq/p/5918599.html
一、浮点数在内存中的表示
对于浮点类型的数据采用单精度类型(float)和双精度类型(double)来存储,float数据占用32bit,double数据占用64bit。不论是float还是double在存储方式上都是遵从IEEE的规范的,float遵从的是IEEE R32.24 ,而double 遵从的是R64.53。
无论是单精度还是双精度在存储中都分为三个部分:
1. 符号位(Sign) : 0代表正,1代表为负
2. 指数位(Exponent): 用于存储科学计数法中的指数数据,并且采用移位存储
3. 尾数部分(Mantissa): 尾数部分
其中float的存储方式如下图所示:

而双精度的存储方式为:

R32.24和R64.53的存储方式都是用科学计数法来存储数据的。因此本文仅仅针对单精度浮点数进行分析,双精度同理可得。
二、单精度浮点数的存储实现
单精度浮点数存储表示
首先来看单精度浮点型float。float占用4字节空间,也就是32位。从左向右数,第1位是符号位(0代表正数,1代表负数),接着是8位指数位,剩下的23位是数据位(实际上有效数字位是24位,因为第一位有效数字总是“1”,不必存储)。如下所示
31 30 23 22 0
S EEEEEEEE DDDDDDDDDDDDDDDDDDDDDDD在这存储实数的四个字节中,将最高地址字节的最高位编号为31,最低地址字节的最低位编号为0,则实数各个部分在这32个二进制位中的分布是这样的:31位是实数符号位,30位是指数符号位,29—23是指数位,22—0位是有效数字位(注意第一位有效数字是不出现在内存中的,它总是“1” )。
单精度浮点数转换步骤
将一个float型转化为内存存储格式的步骤为:
(1)先将这个实数的绝对值化为二进制格式。
(2)将这个二进制格式实数的小数点左移或右移n位,直到小数点移动到第一个有效数字的右边。
(3)从小数点右边第一位开始数出二十三位数字放入第22到第0位。
(4)如果实数是正的,则在第31位放入“0”,否则放入“1”。
(5)如果n是左移得到的,说明指数是正的,第30位放入“1”。如果n是右移得到的或n=0,则第30位放入“0”。
(6)如果n是左移得到的,则将n减去1后化为二进制,并在左边加“0”补足七位,放入第29到第23位。如果n是右移得到的或n=0,则将n化为二进制后在左边加“0”补足七位,再各位求反,再放入第29到第23位。
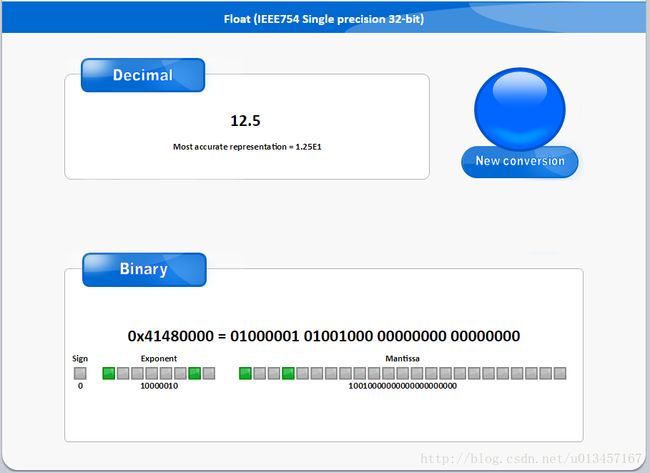
以12.5为例进行说明:
(1)12.5实数绝对值二进制形式是 1100.1。
(2)向左移动3位,转换为科学计数法是1.1001E3,此时n=3。
(3)将小数点右边第一位开始输出23位放入第22到第0位,即数据位D为:
DDDDDDDDDDDDDDDDDDDDDDD
10010000000000000000000(4)12.5为整数,因此第31位放入“0”,即S=0。
(5)n是左移得到的,指数为正,则第30位放入“1”。
(6) n减去1为2,转换为二进制,左边加“0”补足七位,放入第29到第23位。
此时,由(5)(6)得指数位E为:
EEEEEEEE
10000010综上,得到12.5的二进制存储为:
31 30 23 22 0
S EEEEEEEE DDDDDDDDDDDDDDDDDDDDDDD
0 10000010 10010000000000000000000验证
补充:
因为浮点数1.0是一个特殊值,这里特地在这里将解析流程从网上摘抄过来分析:
将实数1.0化为C++的float格式。
(1)将1.0化为二进制后是1.00000000000000000000000。
(2)这时不用移动小数点了,这就是我们在转化方法里说的n=0的情况。
(3)将小数点右边的二十三位有效数字00000000000000000000000放入第22到第0位。
(4)因为1.0是正的,所以在第31位里放入“0”。
(5)因为n=0,所以在第30位里放入“0”。
(6)因为n=0,所以将0补足七位得到0000000,各位求反得到1111111,放入第29到第23位。
完毕。所以实数1.0用C++的float格式表示是:
31 30 23 22 0
S EEEEEEEE DDDDDDDDDDDDDDDDDDDDDDD
0 01111111 00000000000000000000000其中最左边一位是第31位,最右边一位是第0位。
三、存储字节数据转换为单精度浮点数
转换为单精度浮点数步骤
将一个内存存储的float二进制格式转化为十进制的步骤:
(1)将第22位到第0位的二进制数写出来,在最左边补一位“1”,得到二十四位有效数字。将小数点点在最左边那个“1”的右边。
(2)取出第29到第23位所表示的值n。当30位是“0”时将n各位求反。当30位是“1”时将n增1。
(3)将小数点左移n位(当30位是“0”时)或右移n位(当30位是“1”时),得到一个二进制表示的实数。
(4)将这个二进制实数化为十进制,并根据第31位是“0”还是“1”加上正号或负号即可。
同样以12.5的二进制为例:
(1) 在最左边补一位“1”,得到二十四位有效数字。将小数点点在最左边那个“1”右边。
1.10010000000000000000000(2) 取出第29到第23位所表示的值n。由于30位是“1”,所有将n增1为0000011(即n=3)
(3) 由于30位是“1”,将小数点右移3位,得到二进制实数为:
1100. 10000000000000000000(4) 转换为十进制数,由于31位为“0”,所有结果为12.5
四、代码实现
#include