匹配滤波（脉冲压缩）

[TOC]

---

匹配滤波原理

匹配滤波器（match filter）是最佳线性滤波器的一种，该滤波器的准则是输出信噪比最大，常用于通信、雷达等系统的接收机中，下面对其冲激响应/系统函数进行推导。

设该滤波器传递函数为 H(f) ，冲激响应为 h(t) ，输入信号为

r(t)=s(t)+n(t)

其中 s(t) 为输入信号， n(t) 为高斯白噪声。设输入信号的频谱密度函数为 S(f) ，
而高斯白噪声的单边功率谱为 n0/2 ，其中 n0 为高斯白噪声单边功率谱密度。 该信号通过匹配滤波器输出如图1.1所示

图1.1 匹配滤波器

其中 s0(t) 为信号的输出，其大小为

s0(t)=∫+∞−∞H(f)S(f)ej2πftdf

而又已知输出高斯白噪声的功率谱密度等于输入白噪声的功率谱密度乘以系统传递函数模值的平方，即输出噪声功率为

N0=n02∫+∞−∞|H(f)|2df

因此，在采样时刻 t0 上，输出信号瞬时功率和噪声平均功率之比为

r0=|s0(t0)|2N0=|∫+∞−∞H(f)S(f)ej2πftdf|2n02∫+∞−∞|H(f)|2df

利用施瓦兹不等式

|∫+∞−∞f1(x)f2(x)dx|2≤∫+∞−∞|f1(x)|2dx∫+∞−∞|f2(x)|2dx

该等式当且仅当 f1(x)=kf∗2(x) 时取最大值，其中 k 为任意常数。
那么我们认为 f1(x)=H(f) , f2(x)=H(f)ej2πft0 。则有

r0≤∫+∞−∞|H(f)|2df∫+∞−∞|S(f)|2dfn02∫+∞−∞|H(f)|2df=∫+∞−∞|S(f)|2dfn02=2En0

其中 E 为信号的能量。而且当且仅当

H(f)=kS∗(f)e−2πft0

时， r0 取得最大值。
对 H(f) 求逆FFT变换，可得滤波器的冲激响应

h(t)=ks∗(t0−t)

由上式可知匹配滤波器的冲激响应就是信号 s(t) 的镜像，只不过存在一个 t0 的时延。
也可以将匹配滤波的过程理解为一个求相关的过程，当 t0 时刻信号进入滤波器时，与滤波器系数进行卷积，相当于求自相关，很明显要远大于白噪声和滤波器系数的互相关，此时信噪比可达到最大。

---

匹配滤波器仿真

匹配滤波在通信和雷达等系统中有很多应用，其中以雷达系统中的脉冲压缩较为典型，本文以雷达系统中的脉冲压缩(pulse compress)为例，进行仿真。
在雷达目标检测中，希望距离分辨率和探测威力都足够大。而距离分辨率与发射波形的时宽成反比，探测威力（能量）与发射波形的时宽成正比。若发射波形为方波，其时宽 τ 与带宽 B 乘积约等于1，说明距离分辨率和探测威力是相互矛盾的。此时采用线性调频信号，可以很好的解决这个矛盾。其表达式如下：

s(t)=Aej[π(B/τ)t2+ϕ(t)]

其中 A 为幅度， B 为线性调频信号带宽， τ 为线性调频信号时宽。 ϕ(t) 为回波所携带的目标、杂波和噪声的相位。
利用上节对匹配滤波器冲激响应的推导，令 k=1 , t0=0 ,匹配滤波器的系数为

h(t)=s∗(−t)

下面对脉冲压缩进行仿真，仿真参数设置如下

参数	取值	备注
信号带宽	4MHz
信号时宽	200μs
脉冲周期	2ms
采样频率	20MHz
信噪比	20dB
目标距离	T∗fs/2	目标放置在回波中间距离单元处

下图为经过下变频后线性调频信号的实虚部。

图2.1 线性调频信号

下图对回波进行仿真，将目标添加至回波距离中段，并添加高斯白噪声。

图2.2 回波信号


下一步产生匹配滤波器的系数，根据前面理论推导可得滤波器系数幅频特性和相频特性如下。



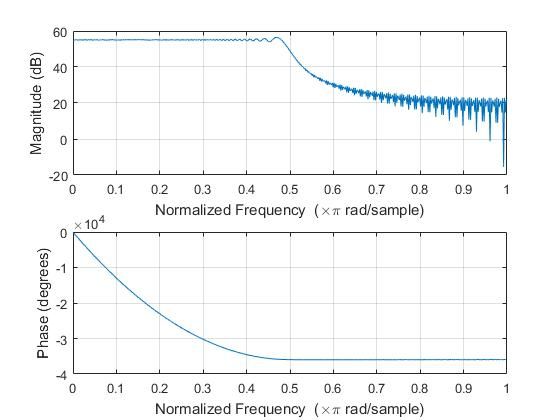
图2.3 滤波器幅/相频特性


由公式可知，滤波器的幅频特性应与线性调频信号幅频特性一致，而相频特性也满足平方律，且相位与线性调频信号相反。
下图为滤波后结果。



图2.4 脉压结果分贝图（不加窗）


滤波后结果近似为 sinc 函数，其主副瓣比为 13.4dB ，而在实际雷达目标检测中，过高的副瓣会导致干扰和杂波对目标提取的影响。故考虑对滤波器系数进行时域加窗，加海明窗，得到如下结果。



图2.4 脉压结果分贝图（加汉明窗）

此时主副比可达到 41.1dB ,但是此时主瓣宽度会有一定的展宽，而且由于加窗的影响，会导致系数失配，造成一定的信噪比损失(标准情况下1.47dB)。

---

匹配滤波器实现

通常采用FPGA或DSP来实现匹配滤波器，具体有时域和频域两种实现方法。
时域实现通常用于采样率不高，滤波器系数点数较少的情况，利用卷积方式完成滤波。通常FPGA中该种方式使用较多，因为采用该种方式，可以对回波进行连续处理，无需对数据进行存储。在乘累加过程中，采用提升运算时钟频率或以面积换时间的方式，可以较好的完成处理。
而当采样率较高的情况下，为节省运算量，通常采用频域的方式完成滤波运算，具体流程图如下。

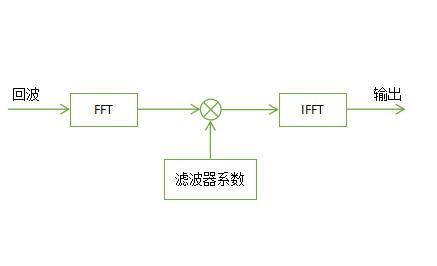
图3.1 频域滤波

频域脉压FPGA实现：
首先将滤波器系数量化后存至ROM，调用FFT IP核完成回波的FFT处理，接着将回波FFT结果与滤波器系数进行点乘，最后再次利用FFT IP核完成点乘结果的IFFT运算（配置成逆FFT方式）。在运算过程中注意定点数的动态问题，及时进行截位。
频域脉压DSP实现：
DSP实现流程与FPGA大致一致，首先将滤波器浮点系数存至内存数组中，并利用FFT函数完成回波信号FFT，接着与系数进行点乘，而某些型号DSP函数库不提供IFFT函数，自己编写一方面比较繁杂，要满足不同点数，另一方面自己编写的函数优化程度可能也不及函数库内的函数。此时可考虑复用FFT函数。具体复用方式见如下推导。
DFT定义：

X(k)=∑n=0N−1x(n)e−j2πkn/N

IDFT定义：

x(n)=1N∑k=0N−1X(k)ej2πkn/N=1N[∑k=0N−1X∗(k)e−j2πkn/N]∗=1NDFT(X∗(k))

由上式可知，将点乘结果取共轭，并调用FFT函数完成FFT运算，最后除以FFT点数即可得到滤波结果。

---

仿真代码附录

%% Pulse Compress
clear all; close all; clc;

% LFM parameter
B       =   4e+6;       % 4MHz带宽
Tao     =   200e-6;     % 200us时宽
T       =   2e-3;       % 2ms脉冲重复周期 
fs      =   8e+6;       %采样频率
SNR     =   20;         % 信噪比20dB
dis     =   T*fs/2;     % 将目标设置在回波中间处

% Generate LFM
t = -round(Tao*fs/2):1:round(Tao*fs/2)-1; % 脉冲采样点 
lfm = (10^(SNR/20))*exp(1i*pi*B/Tao*(t/fs).^2);

figure;
subplot(2,1,1); plot(real(lfm),'b'); title('线性调频信号实部');
subplot(2,1,2); plot(imag(lfm),'r'); title('线性调频信号虚部');

% Generate echo
echo  = zeros(1,T*fs);
echo(dis:1:dis+Tao*fs-1) = lfm;
noise = normrnd(0,1,1,T*fs) + 1i*normrnd(0,1,1,T*fs);
echo = echo + noise;

figure;
subplot(2,1,1); plot(real(echo),'b'); title('回波信号实部');
subplot(2,1,2); plot(imag(echo),'r'); title('回波信号虚部');

% Generate filter coeff
coeff = conj(fliplr(lfm)).* hamming(Tao*fs).'; %翻转共轭/加汉明窗

figure; freqz(coeff);

% pulse compress
fft_n = 2^(floor(log2(T*fs)) + 1);
pc_res = ifft(fft(echo,fft_n).*fft(coeff,fft_n)); % 未截取不完全滤波点

figure;
plot(db(abs(pc_res)/max(abs(pc_res))),'r');  title('脉压结果分贝图');

---

参考文献：
[1] 《通信原理（第七版）》樊昌信，曹丽娜编著；
[2] 《现代雷达系统分析与设计》陈伯孝编著。