sklearn机器学习库学习笔记
1.1广义线性模型
普通最小二乘法
from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit([[0,0],[1,1],[2,2]],[0,1,2])reg.coef_和reg.intercept_中会保存权重参数和初始化参数类型
岭回归
对系数大小增加惩罚项,最小化带惩罚项的残差平方和
>>> from sklearn import linear_model
>>> reg = linear_model.Ridge (alpha = .5)
>>> reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001)
>>> reg.coef_
array([ 0.34545455, 0.34545455])
>>> reg.intercept_
0.13636...设置正则化参数进行广义交叉验证,RidgeCV可以设置cv值触发k折交叉验证
Lasso回归
是拟合稀疏系数的线性模型,一定条件下可以恢复一组非零权重的精确集,相当于加入L1正则化项,因此可以利用它实现L1的特征选择,一般用于稀疏重建和压缩感知。
因此做为多元线性回归中,岭回归是加入L2正则化项,而Lasso回归引入L1稀疏化。
from sklearn import linear_model
reg = linear_model.Lasso(alpha = 0.1)
reg.fit([[0, 0], [1, 1]], [0, 1])
'''
output:
Lasso(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=1000,
normalize=False, positive=False, precompute=False, random_state=None,
selection='cyclic', tol=0.0001, warm_start=False)
'''
reg.predict([[1,1]])
'''
array([ 0.8])
'''其中对于Lasso的正则化参数在sklearn中通过设置LassoCV(坐标下降)和LassoLarsCV(最小角回归)进行更改,其中当样本数量小于特征数量时,利用LassoLarsCV在寻找alpha参数值上更快,更具有优势。
在基于信息标准的模型选择时,估计器 LassoLarsIC 建议使用 Akaike information criterion (Akaike 信息判据)(AIC)或 Bayes Information criterion (贝叶斯信息判据)(BIC),和交叉验证属于同一类别。
多任务Lasso:
MultiTaskLasso是一个估计多元回归稀疏系数的线性模型: y 是一个形状为(n_samples, n_tasks) 的二维数组,其中W中非零的位置,Lasso 产生分散的离散值,而MultiTaskLasso产生的一整列都是非零的。
拟合 time-series model (时间序列模型),强制任何活动的功能始终处于活动状态,其中多任务在数学上的表示是L1和L2的混合正则化器进行训练。
弹性网络:
弹性网络是一种使用L1,L2范数作为先验正则化训练的线性回归模型,同时保留领回归与Lasso回归的性质,可以通过l1_ratio 参数控制 L1 和 L2 的凸组合。
在实践中,Lasso 和 Ridge 之间权衡的一个优势是它允许在循环过程(Under rotate)中继承 Ridge 的稳定性。
进一步可以扩展为多任务弹性网络,MultiTaskElasticNet 是一个对多回归问题估算稀疏参数的弹性网络: Y 是一个二维数组,形状是 (n_samples,n_tasks)。 其限制条件是和其他回归问题一样,是选择的特征,也称为 tasks 。
最小角回归:
最小角回归 (LARS) 是对高维数据的回归算法,逐步回归,在每一步,它都寻找与响应最有关联的预测。当有很多预测有相同的关联时,它并不会继续利用相同的预测,而是在这些预测中找出应该等角的方向。
LARS 模型可以在 Lars ,或者它的底层实现 lars_path或 lars_path_gram中被使用
LassoLars 是一个使用 LARS 算法的 lasso 模型,不同于基于坐标下降法的实现,它可以得到一个精确解,也就是一个关于自身参数标准化后的一个分段线性解。可以通过以下方式进行拟合回归。
reg = linear_model.LassoLars(alpha=.1)贝叶斯回归:
贝叶斯回归可以用于在预估阶段的参数正则化: 正则化参数的选择不是通过人为的选择,而是通过手动调节数据值来实现。
相当于在估计过程中引入新的Alpha变量,通过数据估计得到
上述过程可以通过引入无信息先验到模型中的超参数来完成。 在岭回归中使用的 L2正则项相当于在 w为高斯先验条件,且此先验的精确度为 时,求最大后验估计。在这里,我们没有手工调参数 lambda ,而是让他作为一个变量,通过数据中估计得到。
BayesianRidge 利用概率模型估算了上述的回归问题,其先验参数 w是由以下球面高斯公式得出的:
先验参数 和 一般是服从 gamma 分布 ,这个分布与高斯成共轭先验关系。 得到的模型一般称为 贝叶斯岭回归,并且这个与传统的 Ridge 非常相似。
reg = linear_model.BayesianRidge()逻辑回归LRmodel:
损失函数可以输出单次可能实验结果的概率P,实现了二分类,一对多分类以及多项式回归,并带有可选的L1,L2回归。
其中sklearn默认采用L2正则化项
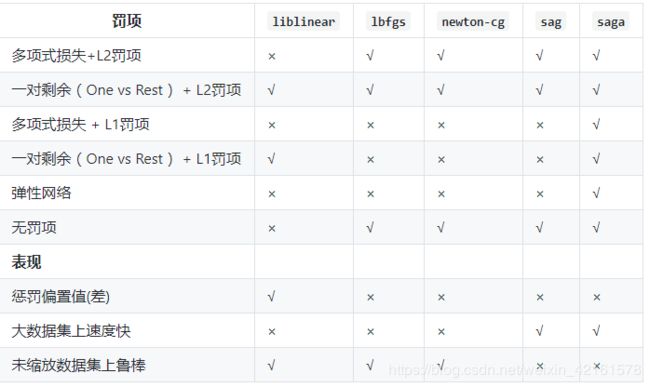
在 LogisticRegression 类中实现了这些优化算法: liblinear, newton-cg, lbfgs, sag(平均随机梯度下降) 和 saga。
不同优化算法在不同规模数据集和是否是真正的多分类任务上还是有一定区别的。
默认情况下,lbfgs求解器鲁棒性占优。对于大型数据集,saga求解器通常更快。对于大数据集,还可以用 SGDClassifier ,并使用对数损失(log loss)这可能更快,但需要更多的调优。
LogisticRegressionCV 对 logistic 回归 的实现内置了交叉验证(cross-validation),可以找出最优的 C和l1_ratio参数 。newton-cg, sag, saga 和 lbfgs 在高维数据上更快,这是因为采用了热启动(warm-starting)
- solver参数决定了我们对逻辑回归损失函数的优化方法,有四种算法可以选择,分别是:
a) liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
b) lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
c) newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
d) sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,适合于样本数据多的时候。
- 从上面的描述可以看出,newton-cg, lbfgs和sag这三种优化算法时都需要损失函数的一阶或者二阶连续导数,因此不能用于没有连续导数的L1正则化,只能用于L2正则化。而liblinear通吃L1正则化和L2正则化。
- 同时,sag每次仅仅使用了部分样本进行梯度迭代,所以当样本量少的时候不要选择它,而如果样本量非常大,比如大于10万,sag是第一选择。但是sag不能用于L1正则化,所以当你有大量的样本,又需要L1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量,要么回到L2正则化。
- 从上面的描述,大家可能觉得,既然newton-cg, lbfgs和sag这么多限制,如果不是大样本,我们选择liblinear不就行了嘛!错,因为liblinear也有自己的弱点!我们知道,逻辑回归有二元逻辑回归和多元逻辑回归。对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。而MvM一般比OvR分类相对准确一些。郁闷的是liblinear只支持OvR,不支持MvM,这样如果我们需要相对精确的多元逻辑回归时,就不能选择liblinear了。也意味着如果我们需要相对精确的多元逻辑回归不能使用L1正则化了。
稳健回归(Robustness regression): 处理离群点(outliers)和模型错误
-
Scikit-learn提供了三种稳健回归的预测器(estimator): RANSAC , Theil Sen 和 HuberRegressor
-
HuberRegressor 一般快于 RANSAC 和 Theil Sen ,除非样本数很大,即
n_samples>>n_features。 这是因为 RANSAC 和 Theil Sen 都是基于数据的较小子集进行拟合。但使用默认参数时, Theil Sen 和 RANSAC 可能不如 HuberRegressor 鲁棒。 -
RANSAC 比 Theil Sen 更快,在样本数量上的伸缩性(适应性)更好。
-
RANSAC 能更好地处理y方向的大值离群点(通常情况下)。
-
Theil Sen 能更好地处理x方向中等大小的离群点,但在高维情况下无法保证这一特点。 实在决定不了的话,请使用 RANSAC
多项式回归:
得的 polynomial regression 与我们上文所述线性模型是同一类(即关于 w 是线性的),因此可以用同样的方法解决。通过用这些基函数建立的高维空间中的线性拟合,该模型具有灵活性,可以适应更广泛的数据范围。
其中本质上相当于将特征[x1.,x2]转化为[1,x1,x2,x12,x1],利用管道pipeline工具创建一个表示简单多项式回归的单个对象,多个二维点的拟合。
>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
... ('linear', LinearRegression(fit_intercept=False))])
>>> # fit to an order-3 polynomial data
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2., 1., -1.])二、调参方法
lighrgbm、RF、Xgboost中的常见调参方法:
1、网格搜索法
GridSearchCV 称为网格搜索交叉验证调参,它通过遍历传入的参数的所有排列组合,通过交叉验证的方式,返回所有参数组合下的评价指标得分,GridSearchCV 函数的参数详细解释如下:
class sklearn.model_selection.GridSearchCV(estimator, param_grid, scoring=None,
fit_params=None, n_jobs=1, iid=True, refit=True, cv=None, verbose=0,
pre_dispatch=‘2*n_jobs’, error_score=’raise’, return_train_score=’warn’) estimator:scikit-learn 库里的算法模型;
param_grid:需要搜索调参的参数字典;
scoring:评价指标,可以是 auc, rmse,logloss等;
n_jobs:并行计算线程个数,可以设置为 -1,这样可以充分使用机器的所有处理器,并行数量越多,有利于缩短调参时间;
cv:交叉验证的折数,默认为3折;
其中在树模型中的参数主要分为两类,树的内部生成参数和外部生成参数
整体上首先将learning rate 和迭代次数确定下来,选择一个较小的步长,确定最优的迭代次数
首先控制树的深度,将depth和再划分所需最小样本作为一组待定解,确定最大深度
而后将再划分所需最小样本和叶子节点最小样本作为一组进行网格搜索
最后确定最大特征数和下采样比例,确定最优解
最后再减小学习率和增加迭代次数来进一步提高精度。一般的调参思路,组合搜索
同时也可以显示特征重要度,说明在构造数据集时的最优特征解
2、Hyperopt 超参数空间优化------贝叶斯优化
自定义函数中引入最小化的目标函数、搜索空间和搜索算法
在参数空间中引入hp.choice和hp.choice()进行搜索空间的选择,同时在搜索过程中相当于引入贝叶斯先验概率,不断调整搜索空间
更进一步的可以将模型本身作为空间参数,返回最优拟合模型和该模型对应的最优参数
参考资料:
https://blog.csdn.net/FontThrone/article/details/85100328
https://www.cnblogs.com/gczr/p/7156270.html
https://blog.csdn.net/qq_41076797/article/details/102941095?utm_medium=distribute.pc_relevant.none-task-blog-baidujs-1