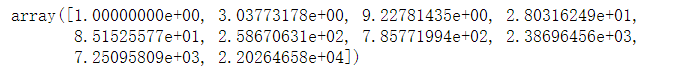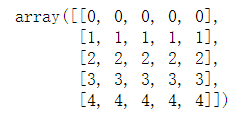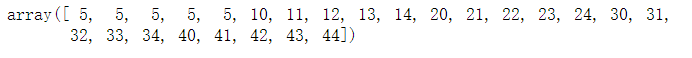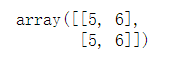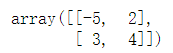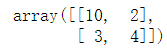Numpy - 多维数据数组
numpy包(模块)几乎总是用于Python中的数值计算。这个软件包为Python提供了高性能的向量、矩阵、张量数据类型。它是在C和Fortran中创建的,因此当计算被矢量化(用矩阵和矢量表示操作)时,性能很高。
目录
1.模块的导入:
2.数组创建numpy
2.1根据列表创建numpy.array
3.使用函数生成数组
3.1arrange
3.2linspace 和 logspace
3.3mgrid
3.4随机数
3.6diag
3.5零和单位矩阵
4.文件导入和导出
4.1逗号分隔的值(CSV)
4.2numpy数组的主要文件格式。
4.3numpy数组的其他属性
5.使用数组
5.1编制索引
5.2选择数组的一部分
5.3先进的索引方法
5.4从数组中提取数据和创建数组的函数。
5.4.1where
5.4.2diag
5.4.3take
5.4.4choose
6.线性代数
6.1点积运算
6.2基础运算
7.矩阵
7.1矩阵
8.数据处理
8.1平均值
8.2标准差和离散度
8.3sum, prod, и trace
8.4多变量数据
9.改变阵列的形状和大小
10.增加一个新的度量newaxis
11.联合
12.hstack and vstack
13.Copy и "deep copy"
14.矩阵的循环
1.模块的导入:
%matplotlib inline
import matplotlib.pyplot as plt
from numpy import *2.数组创建numpy
有几种初始化numpy数组的方法,例如:使用Python的list或tuple。使用旨在创建Numpy数组的函数,如arrange、linspace等。从文件中读取数据(例如Python pickle格式)
2.1根据列表创建numpy.array
v = array([1,2,3,4])
vM = array([[1, 2], [3, 4]])
Mv和M 都是ndarray类型的对象,由numpy模块创建。
type(v), type(M)v数组和M数组的区别在于它们的尺寸(形式)。我们可以使用ndarray.shape属性来获取大小信息。
v.shapeM.shape矩阵中元素的数量可以通过属性ndarray.size
M.size也可以使用numpy方法numpy.shape 和 numpy.size
shape(M)size(M)![]()
numpy.ndarray 看起来像一个普通的 Python 列表。使用它们而不是Python列表有几个原因。
Python的列表是非常常见的。它们可以包含任何对象。他们是动态类型化的。它们不支持矩阵和诗词作品等数学运算。由于动态类型的原因,在Python中用list实现这种操作并不是很有效。
Numpy数组是静态类型化和同质化的。元素类型是在创建数组时定义的(那么数组数据类型可以改变)。
Numpy数组不是很耗费内存。
得益于静态类型化,数学函数如乘积和numpy数组的和可以在编译语言中实现(使用C和Fortran)。
使用ndarray数组的dtype(数据类型)属性,我们可以看到数组的数据类型。
M.dtype试图分配一个错误类型(不一样的类型)的值会导致错误。
M[0,0] = "hello"创建数组时,可以分别指定数据类型。
M = array([[1, 2], [3, 4]], dtype=complex)
M通常使用以下dtype值:int、float、complex、bool、object等。
我们也可以用比特来指定大小:int64、int16、float128、complex128。
3.使用函数生成数组
使用python列表来指定大型数组是不切实际的。你可以使用各种Numpy方法。
3.1arrange
x = arange(0, 10, 1) # arguments: start, stop, step
xx = arange(-1, 1, 0.1)
x3.2linspace 和 logspace
使用linspace,区间的两端都被包括在内,参数:(开始,停止,点的数量)
linspace(0, 10, 25)logspace(0, 10, 10, base=e)3.3mgrid
x, y = mgrid[0:5, 0:5]
x
y
3.4随机数
#导入所需模块
from numpy import random#区间[0,1]内的均匀分布数。
random.rand(5,5)#来自于正态分布的随机数
random.randn(5,5)3.6diag
#对角矩阵
diag([1,2,3])#偏移对角矩阵
diag([1,2,3], k=1) 3.5零和单位矩阵
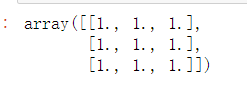
zeros((3,3))ones((3,3))4.文件导入和导出
4.1逗号分隔的值(CSV)
一个非常常见的数据存储格式是CSV,以及类似的格式,如TSV(制表分隔值)。要从这些文件中读取数据,你可以使用以下方法numpy.genfromtxt
data = genfromtxt('stockholm_td_adj.dat')
data.shape
![]()
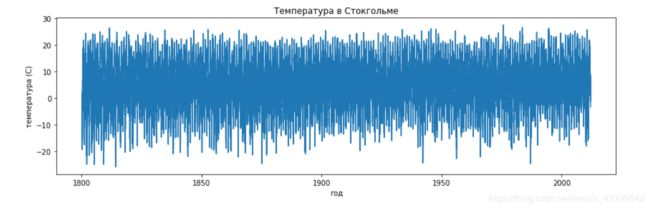
fig, ax = plt.subplots(figsize=(14,4))
ax.plot(data[:,0]+data[:,1]/12.0+data[:,2]/365, data[:,5])
ax.axis('tight')
ax.set_title('Температура в Стокгольме')
ax.set_xlabel('год')
ax.set_ylabel('температура (C)');使用numpy.savetxt我们可以将数组保存在CSV中。
M = random.rand(3,3)
Msavetxt("random-matrix.csv", M)
savetxt("random-matrix.csv", M, fmt='%.5f') # fmt 指定格式4.2numpy数组的主要文件格式。
保存和读取的方法numpy.save 和 numpy.load
save("random-matrix.npy", M)
load("random-matrix.npy")4.3numpy数组的其他属性
M.itemsize#每个byte中的单元数
M.nbytes#byte数目
M.ndim#单位数,计数5.使用数组
5.1编制索引
你可以使用方括号和索引来选择数组的元素。
# v是一个只有一个维度的向量,所以一个索引就足以获得元素。
v[0]# M是一个矩阵(二维数组),所以需要两个索引(行,列)。
M[1,1]如果我们省略了多维数组中的索引,就会返回一些值(一般情况下,N-1维的数组)。
MM[1]M[1,:]#第一行M[:,1]#第一列使用索引,你可以为单个数组元素赋值。
M[0,0] = 1
M也适用于行和列
#也适用于行和列
M[1,:] = 0
M[:,2] = -1
M5.2选择数组的一部分
你可以使用M[lower:uperior:step]语法来获取一个数组的一部分。
A = array([1,2,3,4,5])
AA[1:3]数组的部分是可变的:如果给它们分配新的值,那么从它们提取的数组就会改变原来的数组。
A[1:3] = [-2,-3]
A我们可以省略M[lower:upper:step]中的部分参数。
A[::]#下限、上限、默认步数低于零的指数从数组的末端开始计算。
A = array([1,2,3,4,5])
A[-1]#最后一个元素
A[-3:]#最后三个元素索引分区也适用于多维数组。
A = array([[n+m*10 for n in range(5)] for m in range(5)])
A#方阵
A[1:4, 1:4]#渐进,带有指定间隔数
A[::2, ::2]5.3先进的索引方法
数组的值可以作为选择项目的索引。
row_indices = [1, 2, 3]
A[row_indices]col_indices = [1, 2, -1]
A[row_indices, col_indices]你也可以使用掩码:如果掩码类型为bool,那么根据掩码元素的值与相应的索引,选择该元素(True)或不选择(False)。
B = array([n for n in range(5)])
Brow_mask = array([True, False, True, False, False])
B[row_mask]row_mask = array([1,0,1,0,0], dtype=bool)
B[row_mask]这个函数对于根据某些条件从数组中选择元素非常有用。
x = arange(0, 10, 0.5)
xmask = (5 < x) * (x < 7.5)
maskx[mask]5.4从数组中提取数据和创建数组的函数。
5.4.1where
索引掩码可以通过使用以下方法转换为位置索引 where
indices = where(mask)
indicesx[indices]#这个索引相当于x[mask]的索引。5.4.2diag
使用diag函数还可以提取对角线和子对角线元素。
diag(A)diag(A,-1)![]()
5.4.3take
类似于上述的索引方法。
v2 = arange(-3,3)
v2row_indices = [1, 3, 5]
v2[row_indices]v2.take(row_indices)但take也可以在列表和其他对象上工作。
take([-3, -2, -1, 0, 1, 2], row_indices)5.4.4choose
从多个数组中提取数值。
which = [1, 0, 1, 0]
choices = [[-2,-2,-2,-2], [5,5,5,5]]
choose(which, choices) # 0th elem of 0 array, 1st elem of 1 array, ...
6.线性代数
6.1点积运算
v1 = arange(0, 5)v1 * 2v1 + 2A * 2A + 26.2基础运算
A * Av1 * v1A.shape, v1.shapeA * v17.矩阵
7.1矩阵
dot(A, A)dot(A, v1)dot(v1, v1)也可以将数组转换为矩阵的类型。然后再根据矩阵代数的规律进行+、-、*的算术运算。
M = matrix(A)
v = matrix(v1).T#换位
vM * MM * vv.T * vv + M*v8.数据处理
shape(data)8.1平均值
#温度柱
mean(data[:,3])过去200年,斯德哥尔摩的平均气温在6.2摄氏度左右。
8.2标准差和离散度
std(data[:,3]), var(data[:,3])8.3sum, prod, и trace
d = arange(0, 10)
d#求和
sum(d)#所有元素的乘积
prod(d+1)#累计总和
cumsum(d)#累积乘积
cumprod(d+1)#和diag(A).sum()一样
trace(A)8.4多变量数据
m = random.rand(3,3)
mm.max()#每列最大值
m.max(axis=0)#每行最大值
m.max(axis=1)9.改变阵列的形状和大小
An, m = A.shape
#或者
n,m=np.shape(A)B = A.reshape((1,n*m))
BB[0,0:5] = 5
BA B = A.flatten()
BB[0:5] = 10
B#A没有改变,因为B是A的副本,不是同一个对象的引用。
A10.增加一个新的度量newaxis
v = array([1,2,3])shape(v)#向量 -> 单列矩阵
v[:, newaxis]#尺寸
v[:,newaxis].shapev[newaxis,:].shape11.联合
b = array([[5, 6]])
a = array([[5, 6]])concatenate((a, b), axis=0)concatenate((a, b), axis=1)12.hstack and vstack
vstack((a,b))hstack((a,b))13.Copy и "deep copy"
A = array([[1, 2], [3, 4]])
A#B等同于A
B = A #改变B,将影响A
B[0,0] = 10
BAB = copy(A)#现在改变B将不再影响A
B[0,0] = -5
BA14.矩阵的循环
v = array([1,2,3,4])
for element in v:
print(element)M = array([[1,2], [3,4]])
for row in M:
print("row", row)
for element in row:
print(element)通过枚举,可以同时获得元素的值和索引。
for row_idx, row in enumerate(M):
print("row_idx", row_idx, "row", row)
for col_idx, element in enumerate(row):
print("col_idx", col_idx, "element", element)
# update the matrix M: square each element
M[row_idx, col_idx] = element ** 2#每个元素现在都是列表
M![]()