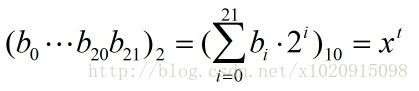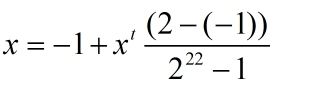遗传算法之二进制编码
title: 遗传算法之二进制编码
tags: 遗传算法
author: Gentleman
新博客地址:遗传算法之二进制编码
遗传算法的基本步骤
遗传算法 GA 的流程如图所示:
编码
把所需要选择的特征进行编号,每一个特征就是一个基因,一个解就是一串基因的组合。为了减少组合数量,在图像中进行分块,然后把每一块看成一个基因进行组合优化的计算。每个解得基因数量是要通过实验确定的。
遗传算法不能直接处理问题空间的参数,必须把它们转换成遗传空间的由基因按一定结构组成的染色体或个体。这一转换操作就叫做编码。评估编码策略常采用以下 3 个规范。
**(1) 完备性(Completeness):**问题空间中的所有点(候选解)都能作为 GA 空间中的点(染色体)表现。
**(2) 健全性(Soundness):**GA 空间中的染色体能对应所有空间中的候选解。
**(3) 非冗余性(Nonredundancy):**染色体和候选解一一对应。
目前几种常用的编码技术有二进制编码、浮点数编码、字符编码、编程编码等。二进制编码是遗传算法中最常见的编码方法,即由二进制字符集 {0, 1} 产生通常的 0, 1 字符串来表示问题的候选解。它具有以下特点:
**
(1) 简单易行;
(2) 符合最小字符集编码原则;
(3) 便于用模式定理进行分析。
**
染色体编码最常用的是二进制编码,对于离散性变量直接进行编码,对于连续性变量先离散化后再编码。
科普1:SPSS常用的基础操作(2)——连续变量离散化
(下面的这个地址中详细介绍了什么是连续变量离散化及其必要性)
人人都是数据咖:http://www.ppvke.com/Blog/archives/44271
科普2:连续特征的离散化:在什么情况下将连续的特征离散化后可以获得更好的效果?
问答来源于知乎:https://www.zhihu.com/question/31989952
举个例子
已知一元函数:
F(x) = xsin(10pi*x)+2 x∈[-1, 2]
现在要求在既定的区间内找出函数的最大值。
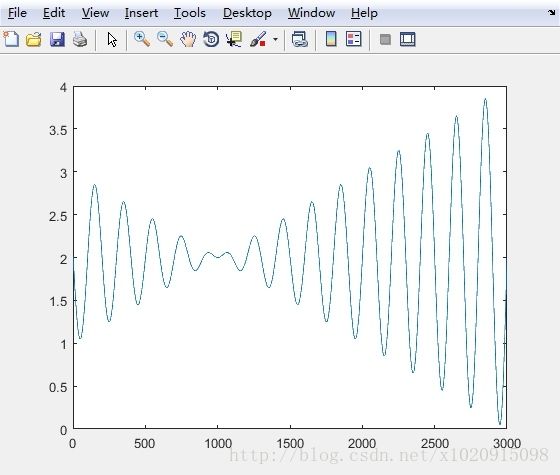
首先我们可以先用 MATLAB 把该函数的图像画出来:
clc, clear;
syms f(x); % 声明函数
x = linspace(-1,2,3000); % 定义 x, x 属于 [-1, 2]
f = x.*sin(10*pi.*x)+2; % 定义函数,因为 x 是向量,所以采用点乘
plot(f); % 画图
然后做出图形如下:
我们可以看到,该图形显示说明该函数具有多个局部最优解,所以适合用遗传算法进行求解。
由遗传算法的基本步骤可知我们第一步应该是编码:
二进制编码
受到人类染色体结构的启发,我们可以设想一下,假设目前只有 0 和 1 两种碱基,我们也用一条链把它们有序的串连在一起,因为每一个单位都能表现出 1bit 的信息量,所以一条足够长的染色体就能为我们勾勒出一个个体特征的所有特征。这就是二进制编码
下面将介绍如何建立二进制编码到一个实数的映射。
明显地,一定长度的二进制编码序列,只能表示一定精度的浮点数。譬如我们要求小数点后精确到六位小数,由于区间长度为
2 - (-1) = 3
为了保证精度的要求,至少把区间 [-1, 2] 分为 3*10^6 等份。又因为
2097152=2^21 < 3*10^6 < 2^22=4194304
所以编码的二进制串至少有 22 位。
把一个二进制串 (b1b2…bn) 转换为区间里面对应的实数值通过下面两个步骤。
(1) 将一个二进制串代表的二进制转换为十进制数:
或许有人并不知道是如何把数值转换到对应区间的实数的,为什么要这么做?我也是问了一下我的小伙伴才知晓的,下面我来简单的说一下:
通常我们归一化到 [0, 1],有时候我们需要归一化到其它区间,这样算一下就可以找到数列的最小值 m 及最大值 M,如果指定的区间是 [a, b],即:
m-->a, M-->b;
系数为:
k = (b-a)/(M-m)
对任意项Xn:变成:
X = a+k(Xn-m)
(二进制编码)
将十进制转换为二进制的 MATLAB 程序代码如下:
%% 将十进制数转换为二进制数(二进制编码)
% @params dec_num 十进制数
% @params N 需保留的二进制小数位数
function bin_num = encode(dec_num, N)
split = '.';
if rem(dec_num, 1) == 0
bin_num = dec2bin(dec_num);
float_num = zeros(1, N);
bin_num = strcat(num2str(bin_num), split);
bin_num = strcat(bin_num, num2str(float_num));
else
remainder = rem(dec_num, 1); % 小数部分
integer = floor(dec_num); % 整数部分
bin_num_int = dec2bin(integer);
i = 1;
flag = true;
while(flag == true)
remainder = remainder*2;
if (i > N) % 是否满足精度
return;
end
if remainder > 1
record(i) = 1;
remainder = rem(remainder, 1);
else if remainder == 1
record(i) = 1;
remainder = rem(remainder, 1);
else
record(i) = 0;
end
i = i+1;
end
bin_num_flt = record;
bin_num = strcat(num2str(bin_num_int), split);
bin_num = strcat(bin_num, num2str(bin_num_flt));
end
end
end
未完…(待续?不存在的)