数据结构 第七章 图

数据结构笔记链接：

第一章 绪论

第二章 线性表

第三章 栈和队列

第四章 串

第五章 数组和广义表

第六章 树和二叉树

第七章 图

第八章 排序

第九章 查找

---

---

7.1 图的基本概念

7.1.1 概念

图G由一个非空项点集V和一个顶点间的关系集合E（边的集合）组成的一种数据结构，可以用二元组定义为：G=(V, E)。

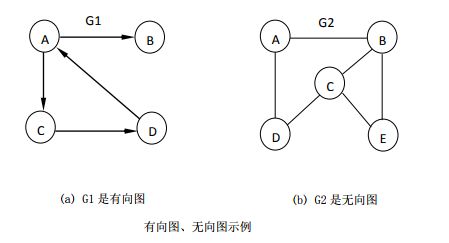
7.1.2 有向图和无向图

在图中，若用箭头标明了边是有方向性的，则称这样的图为有向图，否则称为无向图。

在无向图中，一条边(x, y)与(y, x)表示的结果相同，用圆括号表示。

在有向图中，一条边< x,y >与< y,x >表示的结果不相同，用尖括号表示。

< x,y >表示从顶点x指向顶点y的边，x为始点，y为终点。有向边也称为弧, x为弧尾, y为弧头。则< x,y >表示为一条弧, 而< y,x >表示y为弧尾, x为弧头的另一条弧 。

7.1.3 完全图、稠密图和稀疏图

具有n个顶点，n(n-1)/2条边的图，称为完全无向图；具有n个顶点，n(n-1)条弧的有向图，称为完全有向图。

完全无向图和完全有向图都称为完全图。

当一个图接近完全图时，则称它为稠密图。相反地，当一个图中含有较少的边或弧时(e < nlogn)，则称它为稀疏图。

7.1.4 度、入度、出度和握手定理

在无向图中，关联于该顶点v的边的数目，称为该顶点的度，记为：D(v)。

在有向图中，把以顶点v为终点的边的数目，称为v的入度，记为：ID(v)；

把以顶点v为始点的边的数目，称为v的出度，记为：OD(v)；

顶点v的入度和出度之和称为该顶点的度，D(v)=ID(v)+OD(v)。

握手定理：度之和为边的两倍(有向图中入度必须等于出度等于边的个数)。

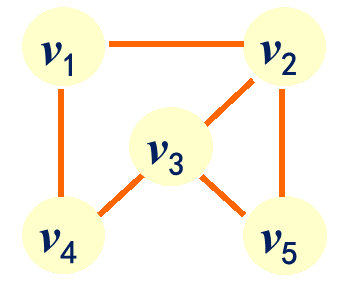
例1：在G1=(V1,E1)中：

V1={v1,v2,v3,v4 ,v5 }
E1={(v1,v2),(v1,v4),(v2,v3),(v2,v5),(v3,v4),(v3,v5)}
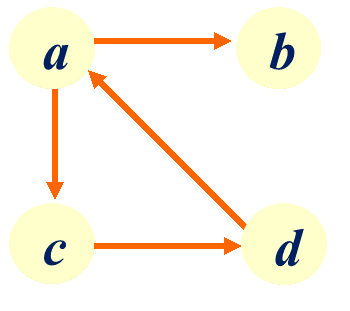
D(v1)=2, D(v2)=3, D(v3)=3, D(v4)=2, D(v5)=2。

例2：在G2=(E2,V2)中：

V2={a,b,c,d}
E2={<a,b>,<a,c>,,a>}
D(a)=ID(a)+OD(a)=1+2=3, 
D(b)=ID(b)+OD(b)=1+0=1, 
D(c) =ID(c)+OD(c)=1+1=2, 
D(d)=ID(d)+OD(d)=1+1=2。

7.1.5 子图

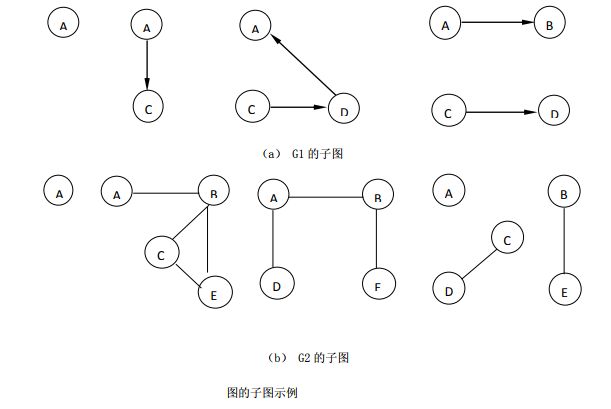
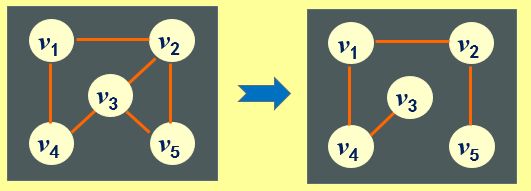
若有两个图G1和G2，G1=(V1, E1)，G2=(V2, E2)，满足如下条件：

即V2为V1的子集，E2为E1的子集，称图G2为图G1的子图。下图给出了7.1.2中图的子图：

7.1.6 权和网

图中每一条边都可以附有一个对应的数值，这种与边相关的数据信息称为权。边上带有权的图称为带权图，也称作网。

7.1.7 路径、路径长度

路径长度是指一条路径上经过的边的数目。若一条路径上除开始点和结束点可以相同外，其余顶点均不相同，则称此路径为简单路径。

例如7.1.4中v1→v2→v5与v1→v4→v3→v5是从顶点v1到顶点v5的两条路径，路径长度分别为2和3。

7.1.8 回路和简单路径

若一条路径上的开始点与结束点为同一个顶点，则此路径被称为回路或环。开始点与结束点相同的简单路径被称为简单回路或简单环。

例如7.1.4中a→c→d→a为简单回路或简单环。

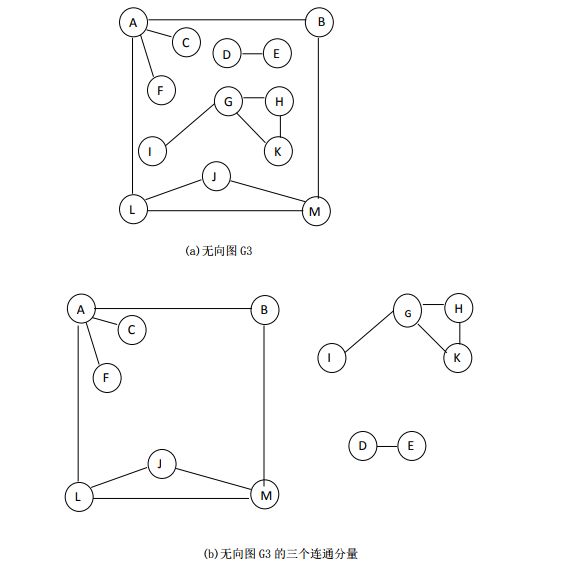
7.1.9 连通图

在无向图 G=（V，{E}）中，若从 vi到 vj有路径相通，则称顶点 vi与 vj是连通的。如果对于图中的任意两个顶点 vi、vj∈V，vi，vj都是连通的，则称该无向图 G 为连通图。无向图中的极大连通子图称为该无向图的连通分量。

在有向图 G=（V，{A}）中，若对于每对顶点 vi、vj∈V 且 vi≠vj，从 vi 到 vj和 vj到 vi都有路径，则称该有向图为强连通图。有向图的极大强连通子图称做有向图的强连通分量。

显然，强连通图只有一个强连通分量，即本身，非强连通图有多个强连通分量。

7.1.10 生成树、生成森林

连通图G的生成树，是G的包含其全部n个顶占的一个极小连通子图,它必定包含且仅包含G的n-1条边。

在非连通图G中，由每个连通分量都可以得到一个极小连通子图（一棵生成树）。这些连通分量的生成树就组成了一个非连通图的生成森林。

7.2 图的存储

7.2.1 邻接矩阵

7.2.1.1 图的邻接矩阵表示

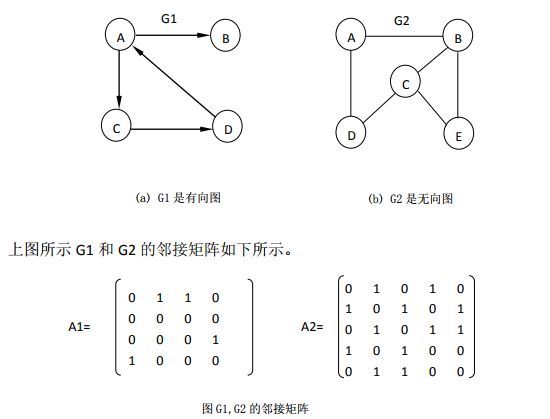
在邻接矩阵表示中，除了存放顶点本身信息外，还用一个矩阵表示各个顶点之间的关系。若(i,j)∈E(G) 或 < i,j >∈E(G)，则矩阵中第i行第j列元素值为1，否则为0 。

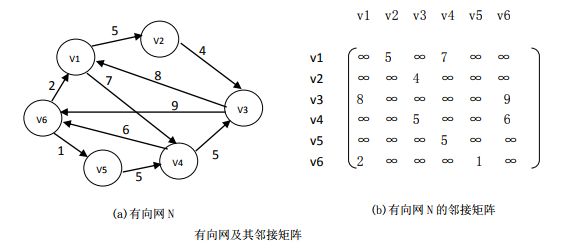
7.2.1.2 网的邻接矩阵表示

类似地可以定义网的邻接矩阵：

7.2.1.3 语言描述

#define n 6     /* 图的顶点数*/
#define e 8     /* 图的边数*/
typedef char vextype;   /* 顶点的数据类型*/
typedef float adjtype;  /* 权值类型*/

typedef struct{ 
vextype vexs[n];    /* 存储顶点信息*/
    adjtype arcs[n][n];     /* 邻接矩阵~存储边的信息*/
} graph;    /* 图的定义*/

算法时间复杂度：O(n×n)

7.2.2 邻接表

7.2.2.1 定义

图的邻接矩阵表示法虽然有其自身的优点，但对于稀疏图来讲，用邻接矩阵的表示方法会造成存储空间的很大浪费，为此引入邻接表表示法。

邻接表表示法实际上是图的一种链式存储结构，它包括两部分：

• 单链表，用来存放边的信息

• 数组，主要用来存放顶点本身的数据信息

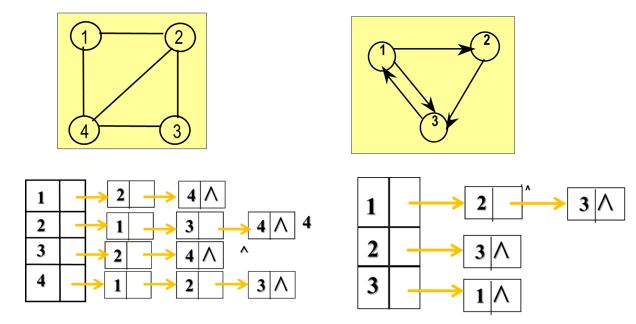
下图为某网的邻接表和网络图的示例：

7.2.2.2 优缺点

优点：空间效率高；容易寻找顶点的邻接点。

缺点：判断两顶点间是否有边或弧，需搜索两结点对应的单链表，没有邻接矩阵方便。

7.2.2.3 语言描述

typedef char vextype;       /*顶点的数据类型*/
    typedef struct  node{  
    int adjvex;             /*邻接点域 */
    int weight;             /*权值域*/
    struct  node  *next ;   /*链域*/
}edgenode;                  /*边表结点*/

typedef struct {
    vertype  vertex;        /*顶点信息*/
    edgenode  *link;        /*边表头指针*/
}vexnode;                   /*顶点表结点*/

vexnode ga[n];              /*存储顶点信息一维表 */

7.2.3 比较

（1）联系
邻接表中每个链表对应于邻接矩阵中的一行，链表中结点个数等于一行中非零元素的个数。

（2）区别
对于任一确定的无向图，邻接矩阵是唯一的(行列号与顶点编号一致)，但邻接表不唯一(链接次序与顶点编号无关)。

邻接矩阵的空间复杂度为O(n²)，而邻接表的空间复杂度为O(n+e)。

（3）用途
邻接矩阵多用于稠密图的存储，而邻接表多用于稀疏图的存储。

7.3 图的遍历

为避免同一顶点被多次访问，必须为每个被访问的顶点作一标志。为此引入一辅助数组，记录每个顶点是否被访问过。

设置一个全局型标志数组visited[0..n-1 ]来标志某个顶点是否被访问过，未访问的值为 0，访问过的值为 1。

7.3.1 深度优先搜索遍历

7.3.1.1 步骤

首先访问顶点v_i，并将其访问标志置为访问过，即visited[i]=1。

然后搜索与顶点v_i有边相连的下一个顶点v_j ，若v_j未被访问过，则访问它，并将v_j的访问标志置为访问过，visited[j]=1，然后从v_j开始重复此过程；若v_j已访问，再看与v_i有边相连的其它顶点。

若与v_i有边相连的顶点都被访问过，则退回到前一个访问顶点并重复刚才过程，直到图中所有顶点都被访问完为止。

7.3.1.2 邻接矩阵实现

算法描述如下所示

void dfs (int i) {          // 从顶点i 出发遍历
    int j;
    visit(i);               //输出访问顶点
    visited[i]=1;           //全局数组访问标记置1表示已经访问
    for(j=1; j<=n; j++)
        if ((A[i][j]==1) && (!visited[j]))
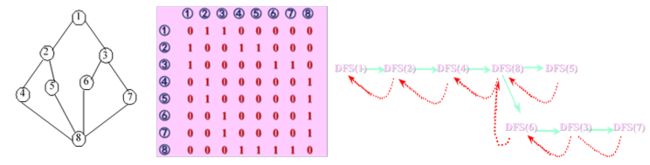
            dfs(j); 
}

上图描述从顶点1出发的深度优先搜索遍历过程，其中实线表示下一层递归调用，虚线表示递归调用的返回。得到从顶点1的遍历结果为: 1, 2, 4, 8, 5, 6, 3, 7。

7.3.1.3 邻接表实现

算法描述如下所示：

void  dfsl(int i) {                 //从V i+1出发深度优先搜索图gl，gl用邻接表表示
    edgenode *p;
    visit(gl[i].vertex) ;           // 输出访问顶点
    visted[i]=1;                    // 全局数组访问标记置为1表示已访问
    p=gl[i].link;                   // 取V i+1的边表头指针
    while (p!=NULL) {               // 依次搜索V i+1的邻接点
        if  (!visited[p->adjvex]) 
            fsl (p->adjvex);        //从V i+1的未曾访问的邻接点出发进行DFS
        p=p->next;                  //找V i+1的下一个邻接点
    }
}

上图描述从顶点7出发的深度优先搜索遍历，其中实线表示下一层递归，虚线表示递归返回，箭头旁边数字表示调用的步骤。从顶点7出发的深度优先搜索遍历序列： 7, 3, 1, 2, 4, 8, 5, 6。

7.3.2 广度优先搜索遍历

和深度优先搜索类似，在遍历的过程中也需要一个访问标志数组。

并且，为了顺次访问路径长度为2、3、…的顶点，需附设队列以存储已被访问的路径长度为1，2，…的顶点。

7.3.2.3 步骤

首先访问顶点i，并将其访问标志置为已被访问，即visited[i]=1；

接着依次访问与顶点i有边相连的所有顶点W₁，W₂，…，W_t；

然后再按顺序访问与W₁，W₂，…，W_t有边相连且未曾访问过的顶点；依此类推，直到图中所有顶点都被访问完为止。

7.3.2.3 邻接矩阵实现

算法描述如下所示：

void  bfs( int  k) {  
    //从顶点V k+1出发广度优先搜索图g，图g用邻接矩阵表示，visited为访问标志向量
    int  i, j ;
    SETNULL(Q);                 //设置空队列Q
    printf(“%c”, g.vexs[k]);        //访问出发点V k+1
    visited[k]=1 ;              //标记置1表示已经访问
    ENQUEUE(Q, K) ;             //已访问过的顶点入队列
    while (!EMPTY(Q)){
        i=DEQUEUE(Q) ;          //队头元素出队列
        for (j=0; jif ( (g.arcs[i][j]==1) && (!visited[j]) ) {
                printf(“%c”, g.vexs[j]);  vsited[j]=1 ;
                ENQUEUE(Q, j); 
            } 
    }
}

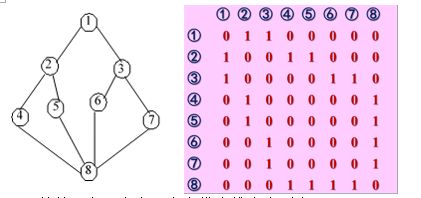
若从顶点1出发，广度优先搜索序列为：1，2，3，4，5，6，7，8

若从顶点3出发，广度优先搜索序列为：3，1，6，7，2，8，4，5

7.3.2.3 邻接表实现

算法描述如下所示：

void  bfsl (int k) {
    //从V k+1出发深度优先搜索图gl，gl用邻接表表示
    int i;
    edgenode *p;
    SETNULL(Q);                             //设置空队列Q
    printf(“%c”, gl[k].vertex);
    visited[k]=1 ;
    ENQUEUE(Q, k) ;
    while (!EMPTY(Q)){
        i=DEQUEUE(Q) ;                      //队头元素出队列
        p=gl[i].link;                       //取V k+1的边表头指针
        while (p!=NULL){                    //依次搜索V k+1的邻接点
            if (!visited[p->adjvex]) {
                printf(“%c”, gl[p->adjvex].vertex);
                visited[p->adjvex]=1;
                ENQUEUE(Q, p->adjvex) ;     //访问过的顶点入队
            }
            p=p->next; //找V i+1的下一个邻接点
        }
    }
}

若从顶点1出发，广度优先搜索序列为：1，2，3，4，5，6，7，8

若从顶点7出发，广度优先搜索序列为：7，3，8，1，6，4，5，2

7.4 生成树与最小生成树

7.4.1 生成树

连通图G的一个极小连通子图，它含有图中n个顶点，但只有n-1条边。

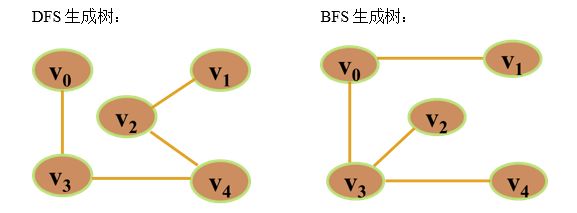
由深度优先搜索遍历得到的生成树，称为深度优先生成树(DFS生成树)。

由广度优先搜索遍历得到的生成树，称为广度优先生成树(BFS生成树)。

例1：画出下图的最小生成树（从V₀出发）

例2：画出下图的最小生成树

7.4.2 最小生成树

生成树中每条边上权值之和达到最小，称为最小生成树。

7.4.2.1 构造准则

• 必须只使用该网络中的边来构造最小生成树；

• 必须使用且仅使用n-1条边来联结网络中的n个顶点；

• 不能使用产生回路的边。

7.4.2.2 Prim算法

• 假设G=是连通图，TE是G上最小生成树中边的集合。

• 算法从U={u0}(u0∈V)，TE={ }开始，任取一个顶点u0作为开始点。

• 重复执行下述操作：在所有u∈U, v∈V-U的边(u,v)∈E中找一条代价最小的边(u0,v0)并入集合TE，同时v0并入U，直至U=V为止。

注意：选择最小边时，可能有多条同样权值的边可选，此时任选其一。

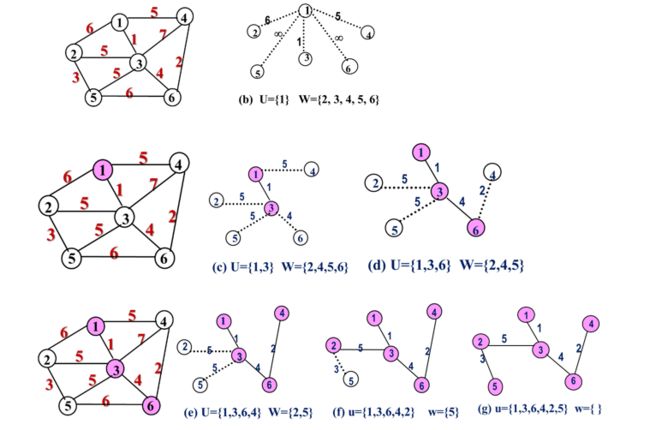
例：假设开始顶点就选为顶点1，故首先有U={1}，W=V-U={2, 3, 4, 5, 6}：

//时间复杂度O(n×n)
struct {
    VertexData adjvex;
    int lowcost;
} closedge[MAX_VERTEX_NUM]; /* 求最小生成树时的辅助数组*/

/*从顶点 u 出发，按普里姆算法构造连通网 gn 的最小生成树，并输出生成树的每条边*/
MiniSpanTree_Prim(AdjMatrix gn, VertexData u) {
    k = LocateVertex(gn, u);
    closedge[k].lowcost = 0; /*初始化，U={u} */

    /*对 V-U 中的顶点 i，初始化 closedge[i]*/
    for (i = 0; i < gn.vexnum; i++){
        if ( i!= k) { 
            closedge[i].adjvex = u;
            closedge[i].lowcost = gn.arcs[k][i].adj;
        }
    }

    /*找 n-1 条边(n= gn.vexnum) */
    for (e = 1; e <= gn.vexnum-1; e++) {
        k0 = Minium(closedge); /* closedge[k0]中存有当前最小边（u0,v0）的信息*/
        u0 = closedge[k0].adjvex; /* u0∈U*/
        v0 = gn.vertex[k0] /* v0∈V-U*/
        printf(u0, v0); /*输出生成树的当前最小边（u0,v0）*/
        closedge[k0].lowcost = 0; /*将顶点 v0 纳入 U 集合*/

        /*在顶点 v0 并入 U 之后，更新 closedge[i]*/
        for (i = 0 ; i < vexnum; i++) {
            if ( gn.arcs[k0][i].adj < closedge[i].lowcost) { 
                closedge[i].lowcost = gn.arcs[k0][i].adj;
                closedge[i].adjvex = v0;
            }
        }
    }
 }

7.4.2.3 Kruskar算法

• 假设G=是连通图，则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=。

• 从E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入到T中，否则舍去此边选择下一条代价最小的边。依次类推，直至T中所有顶点都在同一连通分量上为止。

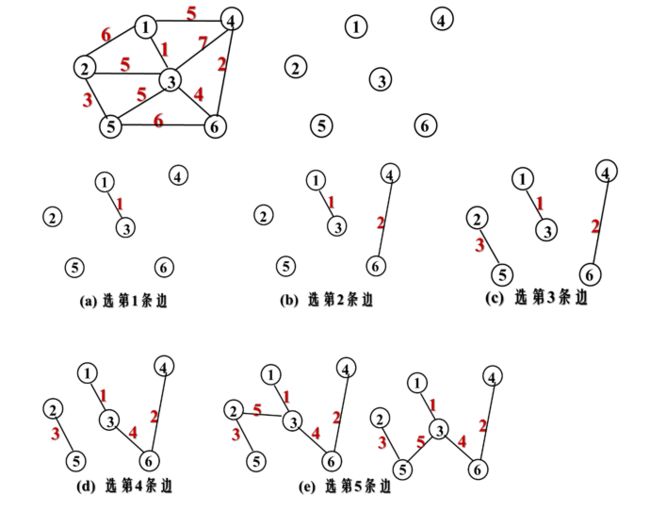
例：用Kruskar算法求最小生成树。

// 邻接矩阵
typedef struct _graph {
    char vexs[MAX];       // 顶点集合
    int vexnum;           // 顶点数
    int edgnum;           // 边数
    int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;

// 边的结构体
typedef struct _EdgeData {
    char start; // 边的起点
    char end;   // 边的终点
    int weight; // 边的权重
}EData;

void kruskal(Graph G) {
    int i,m,n,p1,p2;
    int length;
    int index = 0;          // rets数组的索引
    int vends[MAX]={0};     // 用于保存"已有最小生成树"中每个顶点在该最小树中的终点。
    EData rets[MAX];        // 结果数组，保存kruskal最小生成树的边
    EData *edges;           // 图对应的所有边

    // 获取"图中所有的边"
    edges = get_edges(G);
    // 将边按照"权"的大小进行排序(从小到大)
    sorted_edges(edges, G.edgnum);

    for (i=0; i// 获取第i条边的"起点"的序号
        p2 = get_position(G, edges[i].end);     // 获取第i条边的"终点"的序号

        m = get_end(vends, p1);                 // 获取p1在"已有的最小生成树"中的终点
        n = get_end(vends, p2);                 // 获取p2在"已有的最小生成树"中的终点

        // 如果m!=n，意味着"边i"与"已经添加到最小生成树中的顶点"没有形成环路
        if (m != n) {
            vends[m] = n;                       // 设置m在"已有的最小生成树"中的终点为n
            rets[index++] = edges[i];           // 保存结果
        }
    }

    free(edges);

    // 统计并打印"kruskal最小生成树"的信息
    length = 0;

    for (i = 0; i < index; i++)
        length += rets[i].weight;
    printf("Kruskal=%d: ", length);

    for (i = 0; i < index; i++)
        printf("(%c,%c) ", rets[i].start, rets[i].end);
    printf("\n");
}

7.5 最短路径

如果将交通网络画成带权图，结点代表地点，边代表城镇间的路，边权表示路的长度，则经常会遇到如下问题：两给定地点间是否有通路？如果有多条通路，哪条路最短？

还可以根据实际情况给各个边赋以不同含义的值。例如，对司机来说，里程和速度是他们最感兴趣的信息；而对于旅客来说，可能更关心交通费用。有时，还需要考虑交通图的有向性，如航行时，顺水和逆水的情况。

带权图的最短路径是指两点间的路径中边权和最小的路径。

7.5.1 Dijkstra算法

给定一个出发点(单源点)和一个有向网G=(V, E), 求出源点到其它各顶点之间的最短路径。

7.5.1.1 算法思想

（1）把图中顶点集合分成两组，第一组为集合S，存放已求出其最短路径的顶点，第二组为尚未确定最短路径的顶点集合是V-S(令W=V-S)，其中V为网中所有顶点集合。

（2）按最短路径长度递增的顺序逐个把W中的顶点加到S中，直到S中包含全部顶点，而W为空。

（3）在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到W中任何顶点的最短路径长度。

（4）此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，W中的顶点的距离从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

7.5.1.2 实现步骤

（1）初始时，S只包含源点，S={v}，v的距离为0。U包含除v外的其他顶点，U中顶点的距离为顶点的权或∞ 。

（2）从U中选取一个距离最小的顶点k，把k加入到S中。

（3）以k 作为新考虑的中间点，修改 U中各顶点的距离。

（4）重复步骤（1）、（2）直到所有顶点都包含在S中。

7.5.1.3 例题

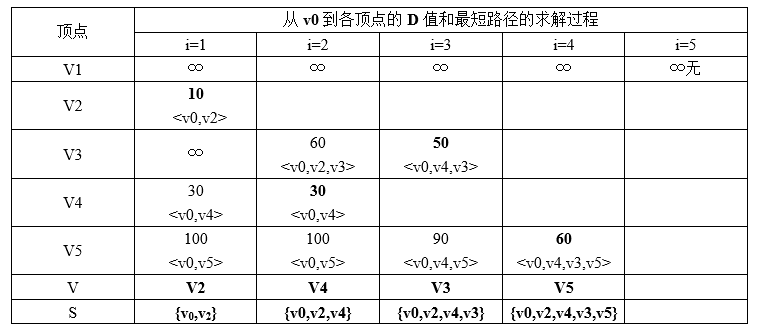
求v0到其它各点的最短路径：

所以最短路径为（V0,V2,V4,V3,V5）。

7.5.1.4 算法实现

#define INFINITY 32768 /*表示极大值，即∞ */

typedef unsigned int WeightType;
typedef WeightType AdjType;
typedef SeqList VertexSet;

/* path[i]中存放顶点 i 的当前最短路径。dist[i]中存放顶点 i 的当前最短路径长度*/
ShortestPath_DJS(AdjMatrix g, int v0,WeightType dist[MAX_VERTEX_NUM], VertexSet path[MAX_VERTEX_NUM] ) { 
    VertexSet s; /* s为已找到最短路径的终点集合 */

    /* 初始化 dist[i]和 path [i] */
    for ( i =0;iif ( dist[i] < INFINITY) {
            AddTail(&path[i], g.vertex[v0]); /* AddTail 是表尾添加操作*/
            AddTail(&path[i], g.vertex[i]);
        }
    }

    InitList(&s);
    AddTail(&s, g.vertex[v0]); /* 将 v0 看成第一个已找到最短路径的终点*/

    /*求 v0 到其余 n-1 个顶点的最短路径(n= g.vexnum )*/
    for ( t = 1; t<=g.vexnum-1; t++) {
        min= INFINITY;
        for ( i =0; iif (! Member(g.vertex[i], s) && dist[i]/*修正 dist[i], i∈V-S */
        for ( i =0; iif (!Member(g.vertex [i], s) && g.arcs[k][i].adj!= INFINITY && (dist[k]+ g.arcs [k][i].adj/* path[i]=path[k]∪{Vi} */
            }
        }
    }
}

7.5.2 Floyd算法

Dijkstra算法只能求出源点到其它顶点的最短路径，欲求任意一对顶点间的最短路径，可以
用每一顶点作为源点，重复调用狄杰斯特拉算法 n 次，其时间复杂度为 O(n³)。

下面介绍一种形式更简洁的方法，即Floyd算法，其时间复杂度也是 O(n³)。

7.5.2.1 算法思想

Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释。

从任意节点i到任意节点j的最短路径不外乎两种可能，一是直接从i到j，二是从i经过若干个节点k到j。

所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

7.5.2.2 实现步骤

（1）从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。 　　

（2）对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

7.5.2.3 算法实现

typedef SeqList VertexSet;

/* g 为带权有向图的邻接矩阵表示法， path [i][j]为 vi到 vj的当前最短路径，dist[i][j]为 vi到vj的当前最短路径长度*/
ShortestPath_Floyd(AdjMatrix g, WeightType dist [MAX_VERTEX_NUM] [MAX_VERTEX_NUM], VertexSet path[MAX_VERTEX_NUM] [MAX_VERTEX_NUM] ) {
     /* 初始化 dist[i][j]和 path[i][j] */
    for (i=0; ifor (j =0;jif (dist[i][j]for (k =0;kfor (i =0;ifor (j=0;jif (dist[i][k]+dist[k][j]/* JoinList 是合并线性表操作 */
}

7.6 拓扑结构与AOV网

7.6.1 AOV网

在一个有向图中，若用顶点表示活动，有向边表示活动间先后关系，则称该有向图叫做顶点活动网(Activity On Vertex network)，简称为AOV网。

在AOV网中，若从顶点i到顶点j之间存在一条有向路径，称顶点i是顶点j的前驱，或者称顶点j是顶点i的后继。

若< i,j >∈G(E)，则称顶点i是顶点j的直接前驱，顶点j是顶点i的直接后继。

7.6.2 拓扑排序

给出有向图G=(V,E)，对于V中的顶点的线性序列(v_i1,v_i2,…,v_in)，如果满足如下条件：若在G中从顶点 v_i到v_j有一条路经，则在序列中顶点v_i必在顶点 v_j之前；则称该序列为 G的一个拓扑序列(Topological order)。

构造有向图的一个拓扑序列的过程称为拓扑排序(Topological sort)。

拓扑排序实现步骤如下：

（1）从AOV网中选一个入度为0的顶点v且输出之；

（2）从AOV网中删除此顶点v及所有出边；

（3）重复（1）、（2）两步，直到AOV网中不存在无前驱的顶点为止。

7.6.3 说明

（1）AOV网不一定都有拓扑序列。

（2）AOV网中不能出现有向回路(或称有向环)。

判断AOV网是否有有向环的方法是对该AOV网进行拓扑排序，将AOV网中顶点排列成一个线性有序序列，若该线性序列中包含AOV网全部顶点，则AOV网无环；否则，AOV网中存在有向环，该AOV网所代表的工程是不可行的。

7.6.4 例题

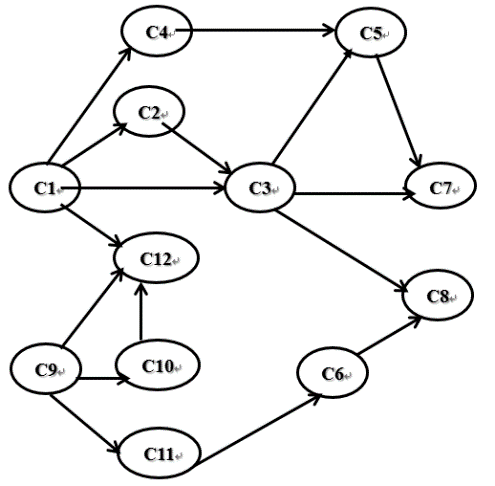
求下图所示的拓扑序列

拓扑序列：

C1–C2–C3–C4–C5–C7–C9–C10–C11–C6–C12–C8

C9–C10–C11–C6–C1–C12–C4–C2–C3–C5–C7–C8

注：一个AOV网的拓扑序列不是唯一的。

7.7 关键路径与AOE网

7.7.1 AOE网

在带权的有向图中，以顶点表示事件，弧表示活动，权表示活动的开销，则称此带权的有向图为用边表示活动的网络，简称AOE网。

在一个表示工程的AOE网中：不存在回路。网中仅存在一个入度为0的顶点，称作源点，它表示了整个工程的开始；网中仅存在一个出度为0的顶点，称为汇点，它表示整个工程的结束。

从源点到汇点的最长路径的长度即为完成整个工程任务所需的时间，该路径叫做关键路径。关键路径上的活动叫做关键活动。

7.7.2 关键路径

把从源点到汇点的最长路径称为关键路径，关键路径上的活动称为关键活动。

在一个AOE网中，可以有不止一条的关键路径。

例：求出下图的关键路径：

上方右图为计算过程，关键路径为：

V1→ V2 →V5 →V7 →V9

V1→ V2 →V5→ V8 →V9

注：从源点到汇点时，选择较大的权值。从汇点到源点时，选择较小的权值。来回均相同的路径就是关键路径。

7.8 例题

7.8.1 例1

有8个结点的无向图最多有【 】条边，最少有【 】条边。

28 ; 7

（注：无向图最多需要n(n-1)/2条边，最少需要n-1条边。有向图最多n(n-1)条边。）

7.8.2 例2

深度优先遍历类似于二叉树的【 】，广度优先遍历类似于二叉树的【 】。

先序遍历 ; 层次遍历

7.8.3 例3

任何一个无向连通图的最小生成树【 】。

不止一棵

7.8.4 例4

求稀疏图的最小生成树，用【 】算法来求解较好。求稠密图的最小生成树，用【 】算法来求解较好。

Kruskar ; Prim

7.8.5 例5

在有向图的邻接矩阵上，第i行中的非零且非无穷元素个数是第i个结点的【 】。

出度

7.8.6 例6

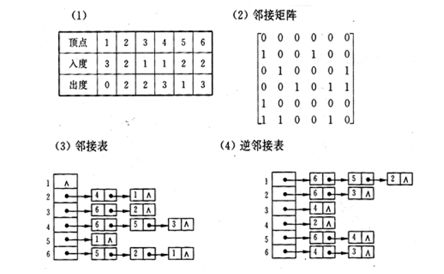
已知下图所示的有向图，请给出该图的:
（1）每个顶点的入/出度；
（2）邻接矩阵；
（3）邻接表；
（4）逆邻接表。

7.8.7 例7

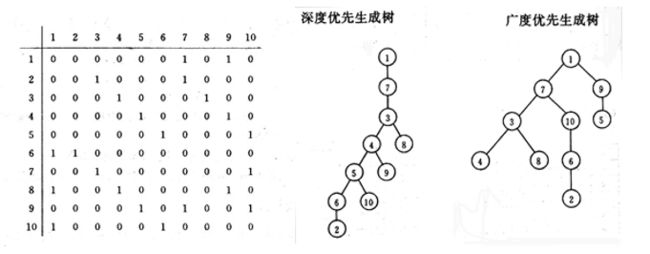
已知二维数组表示的图的邻接矩阵如下图所示。试分别画出自顶点1出发进行遍历所得的深度优先生成树和广度优先生成树。

7.8.8 例8

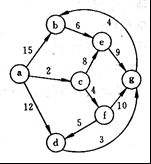
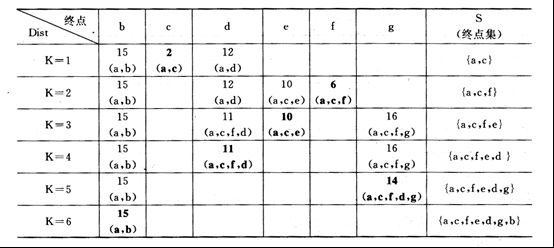
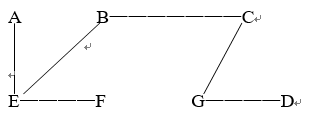
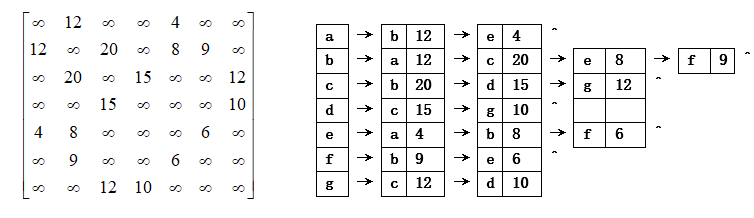
试利用Dijkstra算法求图中从顶点a到其他各顶点间的最短路径，写出执行算法过程中各步的状态。

解：最短路径为：（a,c,f,e,d,g,b）。

7.8.9 例9

给定网G：
（1） 试着找出网G的最小生成树，画出其逻辑结构图。
（2） 用两种不同的表示法画出网G的存储结构图。

解：
（1）最小生成树如下图所示。

（2）邻接矩阵表示和邻接表表示。

---