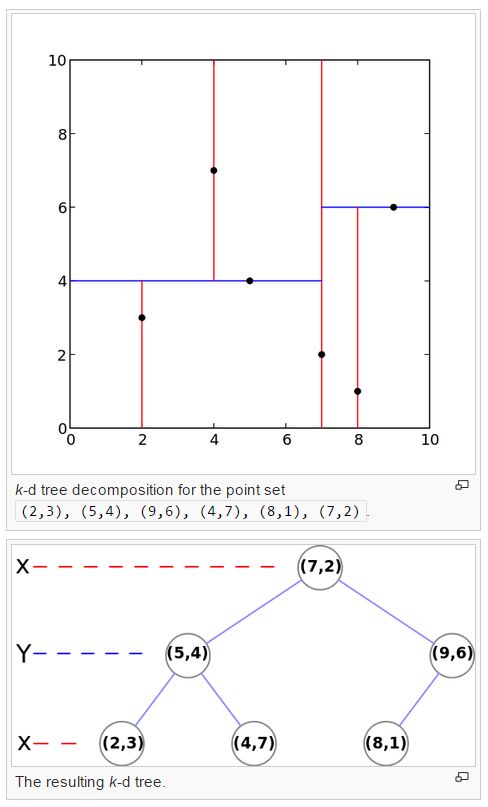
【常用算法】KDTree，局部敏感哈希LSH，在基于最近邻的算法中，当N特别大的时候（TODO）

基于最近邻的算法，在各种情况下经常使用，
比如10万个用户，对每一个用户分别查找最相似的用户，
当N特别大的时候，效率就不是很高，比如当N=10^5，时已经不太好算了，因为暴力法时间复杂度为O(N^2)。


故需要特殊的手段，这里有两个常用的方法， 一个是KDT树（还有Ball Tree），一个是局部敏感哈希（近似算法，得到得是满足一定置信区间的结果）
KDT： O(N*longN)
局部敏感哈希(LSH)：跟桶大小有关


1#  K-Dimensional Tree，KDT， https://en.wikipedia.org/wiki/K-d_tree
用原始样本构造一棵二叉树，

第deep层用第deep % p个特征进行样本划分空间，最后得到一个二叉树，查找的时候依据一定的规则可以实现平均logN的时间复杂度，（跟树挂钩的基本都是logN），

如图：

// TODO

由于之前理解得不是很好，所以写了挺久才实现了。

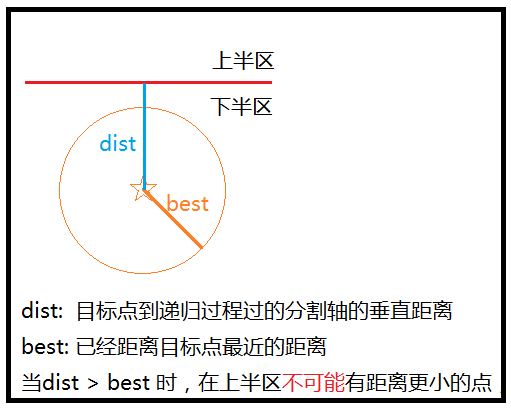
其实核心就是，目标点，到划分轴的距离 >= 当前最小距离，则最小距离不可能在另一半区，所以可以剪枝

即：

样例：

 坐标点：{{7,7},{3,4},{5,3},{1,9},{8,3},{8,2},{10,10}}; 

 目标点：6.5,1

查找过程：

KDT代码：

伪代码：

// 根节点指针， 到目前点的所有特征点，深度(轴)
void insert(Node* &root, vector xList, int deep) {
	// 当前节点为空，则新建一个节点单位，即当前界面+左右孩子节点空指针

	// 拿到x数组，deep轴的中位数
	
	// 把所有点xList划分，median的给右边

	// 分到的点数不为0个，则往相应方向递归插入
}

// 根结点指针，目标点，当前最优，深度(轴)
float query(Node* root, Point p, float best, int deep) {
// 递归三部曲
// 终止处理
// 调用递归
// 向上维护

	// 递归三部曲(1)，终止处理
	// 当前节点为空，则返回无穷大
	// 当前节点左右孩子都为空，即为叶子节点，则计算距离，并返回改距离

	// 递归三部曲(2), 向下调用递归，即考虑的时候把query作为一个已知结果考虑
	// 根据第deep轴判断，向左还是向右递归调用
	// <向左，>向右

	// 递归三部曲(3), 用递归得到的结果进行当前层处理，即向上维护，回溯
	// 计算目标点和当前节点的距离
	// 判断以目标点到当前分位垂直线的距离是否 <= 当前最小距离
	// 若<，则以当前节点的另一个孩子作为跟节点递归调用。
	// 若>, 则不扩展另个孩子，因为在另一边不可能有更小距离的，************************************************剪枝发生在这里
	// 求到当前的距离，左子树最优结果，右子树最优结果，的最小值

	// return 最小的距离
}

实现：

#include
#include
#include
#include
#include
using namespace std;
#define MAXDIST ~(1 << 31)

int countKDT = 0;
struct Point {
	float x[2];
};
struct Node { // 结构体里的数据大小必须是确定的，故vector只能用指针
	vector* xList;
	Node* l;
	Node* r;
};

// 根据x排序
bool cmp0(const Point p1, const Point p2) { // sort(xList.begin(), xList.end(), cmp0);
	return p1.x[0] < p2.x[0];
}
// 根据y排序
bool cmp1(const Point p1, const Point p2) { // sort(xList.begin(), xList.end(), cmp1);
	return p1.x[1] < p2.x[1];
}
// 计算两点距离
float getDist(Point p1, Point p2) {
	if (p1.x[0] == p2.x[0] && p1.x[1] == p2.x[1]) return MAXDIST;
	return sqrt((p1.x[0] - p2.x[0]) * (p1.x[0] - p2.x[0]) + (p1.x[1] - p2.x[1]) * (p1.x[1] - p2.x[1]));
}
// O(n)时间复杂度求中位数
float getMedian(vector a, int l, int r, int k, int deep) {
	// printf("l = %d, r = %d, k = %d\n", l, r, k);
	if (l == r && k == 0) return a[l].x[deep];
	int pl = l;
	int pr = r;
	int tmp = a[l].x[deep];
	while (pl < pr) {
		while (pl < pr && a[pr].x[deep] > tmp) pr--;
		if (pl >= pr) break;
		a[pl++].x[deep] = a[pr].x[deep];
		while (pl < pr && a[pl].x[deep] < tmp) pl++;
		if (pl >= pr) break;
		a[pr--].x[deep] = a[pl].x[deep];
	}
	a[pl].x[deep] = tmp;

	if(pl - l == k) return tmp;
	if(pl - l >  k) {
		return getMedian(a, l, pl - 1, k, deep);
	} else {
		return getMedian(a, pl + 1, r, k - (pl - l + 1), deep);
	}
}

// 建立KDTree
void insert(Node* &root, vector xList, int deep) {
	int i;
	int mid = xList.size() >> 1;
	if (root == NULL) {
		root = (Node*)malloc(sizeof(Node));
		root->l = NULL;
		root->r = NULL;
	}

	vector cur;
	vector left;
	vector right;
	float median;
	// 排序的方法拿到中位数
	if (deep == 0) {
		sort(xList.begin(), xList.end(), cmp0);		
	} else if (deep == 1) {
		sort(xList.begin(), xList.end(), cmp1);
	}
	 median = xList[mid].x[deep];
	 
	 // 基于快排的思想拿到快排
	//median = getMedian(xList, 0 , xList.size() - 1, mid, deep);
	for (i = 0; i < xList.size(); i++) {
		if (xList[i].x[deep] == median) {
			cur.push_back(xList[i]);
		} else if (xList[i].x[deep] < median) {
			left.push_back(xList[i]);
		} else {
			right.push_back(xList[i]);
		}
	}
/*
	//printf("====1===\n");
	for (i = 0; i < left.size(); i++) {
		printf("%d, %d\n", left[i]);
	}
	for (i = 0; i < cur.size(); i++) {
		printf("mid: %d, %d\n", cur[i]);
	}
	for (i = 0; i < right.size(); i++) {
		printf("%d, %d\n", right[i]);
	}
	//printf("====2===\n");
*/

	// root->xList = cur;
	root->xList = new vector; // (vector*)malloc(vector); 报错，因为vector大小未知
	for (i = 0; i < cur.size(); i++) {
		(*(root->xList)).push_back(cur[i]);
	}
	if (left.size() > 0) {
		insert(root->l, left, (deep + 1) % 2);
	} 
	if (right.size() > 0) {
		insert(root->r, right, (deep + 1) % 2);
	}
}

// 打印树
void showTree(Node* root) {
	if(root == NULL) return;
	printf("\nL: ");
	showTree(root->l);
	int i;
	printf("\nM: ");
	for (i = 0; i < (*(root->xList)).size(); i++) {
		printf("%.2f, %.2f\n", (*(root->xList))[i].x[0], (*(root->xList))[i].x[1]);
	}
	printf("\nR: ");
	showTree(root->r);
}

// 查找最近
float query(Node* root, Point p, float best, int deep) {
	if (root == NULL) return MAXDIST;
	//printf("\ncur x = %.2f,%.2f, best =  %.2f, deep = %d\n", (*(root->xList))[0].x[0], (*(root->xList))[0].x[1], best, deep);
	//printf("lc = %d, rc = %d\n", root->l, root->r);	
	int i, j;
	float dist;
	if (root->l == NULL && root->r == NULL) {
		//printf("leaf node \n");
		for (i = 0; i < (*(root->xList)).size(); i++) {
			countKDT++;
			dist = getDist((*(root->xList))[i], p);
			best = dist < best ? dist : best;
		}
		//printf("best = %f\n", best);
		return best;
	}

	// left or right
	if (p.x[deep] <= (*(root->xList))[0].x[deep]) {
		//printf("lll \n");
		best = query(root->l, p, best, (deep + 1) % 2);
	} else {
		//printf("rrr \n");
		best = query(root->r, p, best, (deep + 1) % 2);
	}
	// cur
	for (i = 0; i < (*(root->xList)).size(); i++) {
		countKDT++;
		dist = getDist((*(root->xList))[i], p);
		best = dist < best ? dist : best;
	}
	// another side
	if (best >= fabs(p.x[deep] - (*(root->xList))[0].x[deep])) {
		float distAnother = MAXDIST;
		if (p.x[deep] <= (*(root->xList))[0].x[deep]) {
			//printf("another rrr \n");
			distAnother = query(root->r, p, best, (deep + 1) % 2);
		} else {
			//printf("another lll \n");
			distAnother = query(root->l, p, best, (deep + 1) % 2);
		}
		if (distAnother < best) {
			best = distAnother;
		}
	}
	return best;
}

 float a[][2] = {{7,7},{3,4},{5,3},{1,9},{8,3},{8,2},{10,10}}; // p = 6.5， 1
// float a[][2] = {{2,3}, {5,4}, {9,6}, {4,7}, {8,1}, {7,2}}; //

int main() {
	int i, n;
	n = 200000;	

	// 建立KDTree
	Node* root = NULL;
	vector xList;
	for (i = 0; i < n; i++) {
		Point p;
		p.x[0] = rand() % n;
		p.x[1] = rand() % n;
		//p.x[0] = a[i][0];
		//p.x[1] = a[i][1];
		xList.push_back(p);
		//if(i==0)
		//printf("%.2f,%.2f ", p.x[0], p.x[1]);
	} //printf("\n");
		
	clock_t t1 = clock();
	insert(root, xList, 0);
	clock_t t2 = clock();
	printf("build KDT time = %d\n", t2 - t1);
	//showTree(root);
	//printf("==================================== end of tree\n");

	// KDT 搜索
	Point p;
	p.x[0] = 7;
	p.x[1] = 7;
	float best = MAXDIST;
	float ans = MAXDIST;
	int deep = 0;
	t1 = clock();
	for (i = 0; i < xList.size(); i++) {
		p = xList[i];
		best = query(root, p, MAXDIST, deep);
		ans = ans < best ? ans : best;
	}
	printf("kdtree best = %f\n", best);
	printf("countKDT = %d\n", countKDT);
	t2 = clock();
	printf("KDT time = %d\n", t2 - t1);
	
	// 暴力法
	/*
	t1 = clock();
	float best2 = MAXDIST;
	int count2 = 0;
	for (int j = 0; j < n; j++) {
		p = xList[j];
		best2 = MAXDIST;
		for (i = 0; i < n; i++) {	
			count2++;
			float dist2 = getDist(p, xList[i]);
			if (dist2 < best2) {
				best2 = dist2;
			}
		}
	}
	printf("O(n): best2 = %f\n", best2);
	t2 = clock();
	printf("O(n) time = %d\n", t2 - t1);
	printf("%d\n", count2);
	*/
	return 0;
}
/*
n = 10^4 时，
对每一个点求其最近距离的点
KDT：
	O(nlogn)
	KDT build time = 102ms
	KDT time = 25ms
	exe count = O(nlogn) = 24 * 10^4

暴力法：
	O(n^2)
	time = 4351
	exe count = O(n^2) = 10^8
*/

2# Locality-sensitive hashing，LSH， https://en.wikipedia.org/wiki/Locality-sensitive_hashing
局部敏感哈希其实是一种桶方法，核心思想是当两个样本的相似度比较近的时候，这两个样本更有可能掉到同一个桶里面。
其中有2个要求：
similarity(x1, x2) <= sim1 时，>=p1（大，例如0.95） 的概率使得x1，x2在同一个桶里面
similarity(x1, x2) >   sim2 时，< p2 （小，例如0.05） 的概率使得x1，x2掉在同一个桶里


所以和一般使用的hash函数思想不一样，一般的hash函数希望每个样本hash后尽量的分开，而这里的hash则希望近的样本hash到一个桶里

// TODO