单源最短路径——迪杰斯特拉(Dijkstra)算法 C++实现
求最短路径之Dijkstra算法
Dijkstra算法是用来求单源最短路径问题,即给定图G和起点s,通过算法得到s到达其他每个顶点的最短距离。
基本思想:对图G(V,E)设置集合S,存放已被访问的顶点,然后每次从集合V-S中选择与起点s的最短距离最小的一个顶点(记为u),访问并加入集合S。之后,令u为中介点,优化起点s与所有从u能够到达的顶点v之间的最短距离。这样的操作执行n次(n为顶点个数),直到集合S已经包含所有顶点。
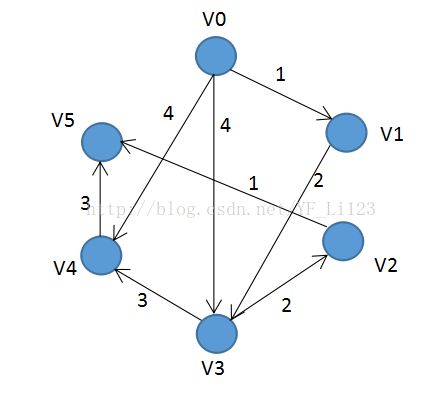
由于图可以使用邻接矩阵或者邻接表来实现,因此会有两种写法。以下图为例来具体实现代码:
代码:
main.cpp
#include
#include
using namespace std;
const int INF = 1e9; // int范围约为 (-2.15e9, 2.15e9)
/*Dijkstra算法解决的是单源最短路径问题,即给定图G(V,E)和起点s(起点又称为源点),边的权值为非负,
求从起点s到达其它顶点的最短距离,并将最短距离存储在矩阵d中*/
void Dijkstra(int n, int s, vector> G, vector &vis, vector &d, vector &pre)
{
/*
* n: 顶点个数
* s: 源点
* G: 图的邻接矩阵
* vis: 标记顶点是否已被访问
* d: 存储源点s到达其它顶点的最短距离
* pre: 最短路径中v的前驱结点
*/
// 初始化
fill(vis.begin(), vis.end(), false);
fill(d.begin(), d.end(), INF);
d[s] = 0;
for (int i = 0; i < n; ++i)
{
pre[i] = i;
}
// n次循环,确定d[n]数组
for (int i = 0; i < n; ++i)
{
// 找到距离s最近的点u,和最短距离d[u]
int u = -1;
int MIN = INF;
for (int j = 0; j < n; ++j)
{
if (!vis[j] && d[j] < MIN)
{
u = j;
MIN = d[j];
}
}
// 找不到小于INF的d[u],说明剩下的顶点与起点s不连通
if (u == -1)
{
return;
}
vis[u] = true;
for (int v = 0; v < n; ++v)
{
// 遍历所有顶点,如果v未被访问 && 可以达到v && 以u为中介点使d[v]更小
if (!vis[v] && G[u][v] != INF && d[u] + G[u][v] < d[v])
{
d[v] = d[u] + G[u][v]; // 更新d[v]
pre[v] = u; // 记录v的前驱顶点为u(新添加)
}
}
}
}
// 输出从起点s到顶点v的最短路径
void DFSPrint(int s, int v, vector pre)
{
if (v == s)
{
cout << s << " ";
return;
}
DFSPrint(s, pre[v], pre);
cout << v << " ";
}
int main()
{
int n = 6;
/*邻接矩阵*/
vector> G = {{ 0, 4,INF,INF, 1, 2},
{ 4, 0, 6,INF,INF, 3},
{INF, 6, 0, 6,INF, 5},
{INF,INF, 6, 0, 4, 5},
{ 1,INF,INF, 4, 0, 3},
{ 2, 3, 5, 5, 3, 0}};
vector vis(n);
vector d(n);
vector pre(n);
Dijkstra(n, 0, G, vis, d, pre);
for (size_t i = 0; i < d.size(); ++i)
{
cout << "the shortest path " << i << " is: " << d[i] << endl;
}
cout << endl;
// v = 2: 0->5->2 cost = 2 + 5 = 7
// v = 3: 0->4->3 cost = 1 + 4 = 5
int v = 2;
DFSPrint(0, v, pre);
cout << endl << "cost = " << d[v] << endl;
return 0;
}
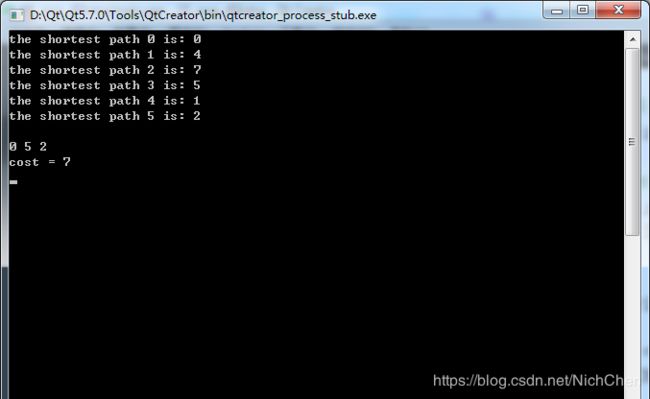
运行结果:
复杂度分析:
主要是外层的循环O(V)(V就是顶点个数n)与内层循环(寻找最小的d[u]需要O(V)、枚举需要O(V)产生的),总的时间复杂度为O(V*(V+V))=O(V^2)
Dijkstra算法与Prim算法的联系:
前者每次寻找与树最近的结点
后者每次寻找与源最近的结点
总结:
Dijkstra算法只能应对所有边权都是非负数的情况,如果边权出现负数,那么Dijkstra算法很可能会出错,这是最好使用SPFA算法。
上面的做法复杂度为O(V^2)级别,其中由于必须把每个顶点都标记已访问,因此外层循环的O(V)时间是无法避免的,但是寻找最小d[u]的过程却可以不必达到O(V)的复杂度,而可以使用对优化来降低复杂度。最简单的写法是直接使用STL中的优先队列priority_queue,这样使用邻接表实现Dijkstra算法的时间复杂度可以降低为O(VlogV+E)。
如果题目给出的是无向边(即双向边)而不是有向边,又该如何解决呢?其实很简单,只需要把无向边当成两条指向相反的有向边即可。对邻接矩阵来说,一条u与v之间的无向边在输入时可以分别对G[u][v]和G[v][u]赋以相同的边权;而对于邻接表来说,只需要在u的邻接表Adj[u]末尾添加上v,并在v的邻接表Adj[v]末尾添加上u即可。
(4)、Dijkstra算法求解实际问题
之前讲的是最基本的Dijkstra算法,那么平时考试笔试等遇到的题目肯定不会这么“裸”,更多时候会出现这样一种情况,即从起点到终点的最短距离最小的路径不止一条。
那么碰到这种两条以上可以达到最短距离的路径,题目就会给出一个第二标尺(第一标尺是距离),要求在所有最短路径中选择第二标尺最优的一条路径,而第二标尺常见的是以下三种出题方法或者其组合:
给每条边在增加一个边权(比如说花费),然后要求在最短路径有多条时要求路径上的花费之和最小(当然如果边权是其它含义,也可以是最大)
给每个点增加一个点权(例如每个城市能收集到的物资),然后在最短路径有多条时要求路径上的点权之和最大(当然如果是其它含义,也可以是最小)
直接问有多少条最短路径
解决思路:都只需要增加一个数组来存放新增的边权或点权或最短路径条数,然后在Dijkstra算法中修改优化d[v]的那个步骤即可,其它部分不需要改动。
如下:
新增边权。以新增的边权代表花费为例,用cost[u][v]表示u->v的花费(由题目输入),并增加一个数组c[],令从起点s到达顶点u的最少花费为c[u],初始化时只有c[s]=0,其余均为INF(一个很大的值),这样就可以在更新d[v]时更新c[v]. 代码如下:
for(int v=0; v
新增点权。以新增的点权代表城市中能收集到的物资为例,用weight[u]表示城市u中的物资数目(由题目输入),并增加一个数组w[],令起点s到达顶点u可以收集到的最大物资为w[u],初始化时只有w[s]为weight[s],其余均为0,这样就可以在更新d[v]时更新w[v].代码如下:
for(int v=0; vw[v])
w[v] = w[u]+weight[v];
}
}
求最短路径条数。只需要添加一个数组num[],令从起点s到达顶点u的最短路径条数为num[u],初始化时只有num[s]=1,其余均为0,这样就可以在更新d[v]时让num[v]=num[u],而当d[u]+G[u][v] =d[v]时,让num[v]+=num[u].代码如下:
for(int v=0; v若需要将多条最短路径打印出来,则需要将记录前驱结点的数组int pre[n]改为二维数组vector
并在查找到相同路径时,采用push_back()同时保存多个前驱结点,而在找到更短路径时,需要clear()清空之前所保持的前驱结点,并再保存当前最短路径下的前驱结点,在打印路径时同样采用DFS即可,保存路径部分代码如下:
for(int v=0; v参考资料:
https://blog.csdn.net/YF_Li123/article/details/74090301
普林斯顿算法公开课:Algorithms - Robert Sedgewick, Kevin Wayne