Leetcode 第197场周赛题解

5460. 好数对的数目

知识点：哈希
设 count[i] 为数字 i 出现的次数，则答案为 count[i]*(count[i]-1)/2 的累加和，i ∈ [1, 100]。
首先遍历 nums 统计每个数字出现的次数，然后遍历 count 计算答案即可。

class Solution {
public:
    int numIdenticalPairs(vector<int>& nums) {
        int count[101] = {0};
        for(auto v : nums) {
            count[v]++;
        }
        int anw = 0;
        for(int i = 1; i <= 100; i++) {
            anw += count[i]*(count[i]-1)/2;
        }
        return anw;
    }
};

5461. 仅含 1 的子串数

知识点：双指针
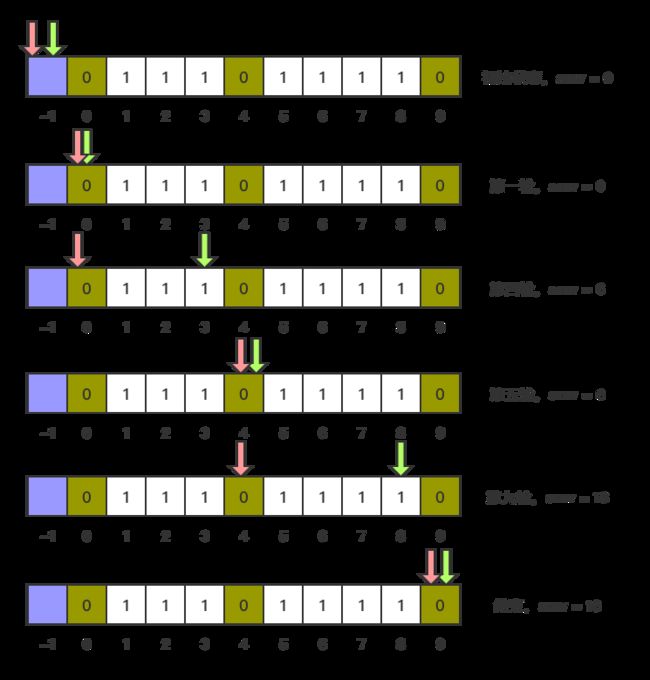
初始时，两个指针 head，tail 都指向 -1 位置。
不停的移动两个指针，直到 tail 指向最后一个字符，每轮移动规则如下：

• 首先将 tail 向后移动一个单位。
• 如果移动后 tail 指向 0 ，那么移动 head 至 tail 处。
• 如果移动后 tail 指向 1，那么累加 tail - head。tail - head 的意义为 以 tail 结尾的仅含 1 的子串的数量

class Solution {
public:
    int numSub(string s) {
        int64_t count = 0;
        for(int prefix = -1, i = 0, n = s.size(); i < n; i++) {
            if(s[i] == '0') {
                prefix = i;
            } else {
                count += i-prefix;
                count %= 1000000007;
            }
        }
        return count;
    }
};

5211. 概率最大的路径

知识点：最短路
典型的最短路问题。只不过路径的权值的计算方式从加法变成了乘法，从最近变成了求最大。但只要不会出现"负环"，即存在有限长度的最优路径，我们就可以借助优先队列+BFS搞定。

Q: 啥情况会出现负环?
A: 比如求权值最小的路径时，存在权值为负的边。只要不停的走这条负边，路径的权值就会不断减小。此时显然不存在有限长度的最优路径。

class Solution {
public:
    vector<pair<double, int>> next[10000];
    double prob[10000];
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        for(int i = 0; i < edges.size(); i++) { // 建立邻接表
            int u = edges[i][0];
            int v = edges[i][1];
            double p = succProb[i];
            next[u].push_back(make_pair(p, v));
            next[v].push_back(make_pair(p, u));
        }
        
        typedef pair<double, int> Data;
        priority_queue<Data, vector<Data>, less<Data>> pq; //借助 less 建立大顶堆，优先按概率排序。
        
        memset(prob, 0, sizeof(double)*n);
        
        prob[start] = 1.0; // 自己到自己的概率肯定是 1。
        pq.push(make_pair(1.0, start)); // 将起点放入队列。
        
        while(pq.empty() == false) {
            auto f = pq.top(); // 从大顶堆中取出当前访问到的概率最大的点。
            pq.pop();
            if(f.first < prob[f.second]) { // 剪枝
                continue;
            }
            for(auto ne : next[f.second]) { // 从 f 继续向周围走一步。
                int next = ne.second; // 下一步可到达的点
                double p = prob[f.second] * ne.first; // 计算从 start 经 f 到 next 的概率。
                if(p > prob[next]) { // 比之前到达 next 的路径更优。
                    prob[next] = p;  // 更新
                    // 虽然可能重复同一个点，但上面的剪枝语句保证了只有最大的那个才会生效。
                    // 而且 if(p > prob[next]) 保证了不可能放入重复的概率。
                    pq.push(make_pair(p, next)); 
                }
            }
        }
        
        return prob[end];
    }
};

5463. 服务中心的最佳位置

知识点：模拟退火；P-median problem

友情链接：P-中位问题_百度百科 模拟退火_百度百科

平面包含无数个点，而我们要从这无数个点中找到一个最优解，这在大多数情况下是不可能的。我们能做的只能是在精度要求范围能找到一个近似最优解。传统的解决方案就是模拟退火。算法流程如下：

1. 选择一个初始点 Start。
2. 选择几个试探的方向，如上下左右。
3. 初始化一个步长 step。
4. 根据试探方向和步长以及 start，可以得到若干的候选点。
5. 如果候选点存在比 start 更优的点，那么更新 start，继续步骤3。
6. 如果候选点都比 start 更差：
   1. 如果步长已小于要求的精度，流程结束，start 即为近似解。
   2. 否则，缩小步长，继续步骤4。

道理我都懂，奈何一直卡精度WA！！果断偷一波大佬的模板！！

const double eps = 1e-8;
const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1};

double calc(double ax, double ay, double bx, double by) {
    double dx = bx - ax, dy = by - ay;
    return sqrt(dx * dx + dy * dy);
}

class Solution {
public:
    double getMinDistSum(vector<vector<int>>& positions) {
        int n = positions.size();
        double x = 0, y = 0;
        auto dist = [&](double cx, double cy) {
            double ans = 0;
            for (auto v : positions) 
                ans += calc(cx, cy, v[0], v[1]);
            return ans;
        };
        double d = dist(x, y);
        double step = 100.0;
        int done = 0;
        while (step > eps) {
            done = 0;
            for (int i = 0; i < 4; ++i) {
                double nx = (double)x + step * dx[i];
                double ny = (double)y + step * dy[i];
                double t = dist(nx, ny);
                if (t < d) {
                    d = t;
                    x = nx;
                    y = ny;
                    done = 1;
                    break;
                }
            }
            if (!done)
                step /= 2;
        }
        
        return d;
    }
};