算法练习day12——190331（哈希函数、哈希表、布隆过滤器、一致性哈希）

1.哈希函数

1.1 特点：

1. 经典的哈希函数输入域是无穷大的。
2. 输出域是有穷尽的；
3. 相同输入得到的输出肯定是一样的；
4. 不同的输入得到的输出也可能一样（输入域>输出域）;
5. 哈希函数的离散型：给定多个不同的输入，得到的输出在输出域上均匀分布。

• 可用来打乱输入规律，输出的规律和输入规律是没有关系的。
• 若输出在整个输出域上均匀分布，那么输出mod m之后得到的结果在0~m-1上也是均匀分布的。

1.2 由给定的一个哈希函数得到1000个互相独立的哈希函数

假设给定哈希函数h，它的输出是16位的。

将其高8位作为h1，低8位作为h2。h1和h2相互独立，因为16位输出中的每一位都和其他位无关。

那么，可构造：

• 
• 
• ...

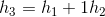
构造的多个哈希函数之间是相互独立的。

2.哈希表

2.1 put(K,V)

hashCode(K)-->h1

将(K,V)放到下标为h1的桶中：

• 若桶不空，则判断有无K；
  • 有，V若不等，则更新V；
  • 无，直接将(K,V)链在此桶元素的后面。

若桶中的链较长，需要扩容。

重新以新容量进行hashCode的运算。

各种操作都是级别的。即使扩容操作费时，但这操作不频繁，也可以押得很低。（还可在离线的时候进行扩容，不占用在线时间）。

JVM中每个桶中放的是一棵红黑树。不太需要扩容。

有一个100T的大文件，其中每一行存的是一个字符串，去掉其中重复的字符串。假设可用的机器为1000台。

具体做法：

用哈希函数作分流——读出每一行字符串，然后进行hashCode计算，之后模1000。这样相同的字符串就会分配到同一台机器。——利用哈希函数可以将100T大文件中的字符串（假设M种 ）按种类平均分配到1000台机器上。

3.设计RandomPool结构

【题目】 设计一种结构， 在该结构中有如下三个功能：

• insert(key)： 将某个key加入到该结构， 做到不重复加入。
• delete(key)： 将原本在结构中的某个key移除。
• getRandom()：等概率随机返回结构中的任何一个key。

【要求】 Insert、 delete和getRandom方法的时间复杂度都是O(1)

3.1 分析

哈希表的结构中：

• 若数据量较少，有的桶可能会没元素，此时无法做到均匀取出（遍历取出的话，复杂度会达到O(N)）
• 若数据量较多，每个桶中的链长度也不是绝对相等的。无法做到等待率。

本题中使用两个哈希表map1和map2实现。

比如A元素是第0个进来的，那么:

• 在map1中就存（A,0）——A是第0个进来的；
• 在map2中存（0,A）——第0个进来的是A。

同时需要有个int型的变量记录某个元素是第几个进来的。

3.1.1 先考虑add()，忽略remove()。

• 若目前进来了26个元素，size=26，此时调用了getRandom()：
  • 使用Math.random()*size生成0~25中随机一个数indexm；
  • 然后在map2中由Key=index找到对应的value，返回 。

3.2.1 remove()

若删除时不做任何操作，则在删除之后，会产生多个“洞”，使得在计算index时无法做到等概率，因为某些位置上没元素。

假设有1000条记录（str0~str999），现在要删除str17，在删除时：

• map1中：将str999放在str17的位置（即，将自己的value改为17即可）；
• map2中：将str999放在17的位置上（即，将自己的key改为17即可，也就是将17对应的value由str17改为str999）；
• 删除map1和map2中的最后一条记录;
• size-1=999.

保证了存储数据位置的连续。

3.2 代码实现

package Hash;

import java.util.HashMap;

public class RandomPoolTest {

	public static class RandomPool{
		HashMap map1;
		HashMap map2;
		int size;
		
		public RandomPool() {
			this.map1=new HashMap<>();
			this.map2=new HashMap<>();
			this.size=0;
		}
		
		public void insert(String str) {
			if(!this.map1.containsKey(str)) {
				this.map1.put(str, this.size);
				this.map2.put(this.size, str);
				this.size++;
			}
		}
		
		public void delete(String str) {
			if(this.map1.containsKey(str)) {
				int index=this.map1.get(str);
				String laststr=this.map2.get(--this.size);
				this.map1.put(laststr, index);
				this.map2.put(index, laststr);
				this.map1.remove(str);
				this.map2.remove(index);
				size--;
			}
		}
		
		public String getRandom() {
			if(size==0)
				return null;
			int index=(int)(Math.random()*size);
			return this.map2.get(index);
		}
	}
}

4.布隆过滤器

4.1 简介

应用场景：判断某一个东西是否在一个集合中（布隆过滤器本身就是一个集合）

举例：看一个url是否在已有的黑名单（100亿个64字节的url）中，在返回true，不在返回false。

若使用哈希函数，不存value，则使用HashSet，最起码需要6400亿字节（640G）才能把所有的黑名单url装下。

缺点：有失误率

• 若一个url确实属于黑名单，则它肯定返回true；
• 若一个url不在黑名单中，可能返回true，也可能返回false。

布隆过滤器是一个比特类型的map

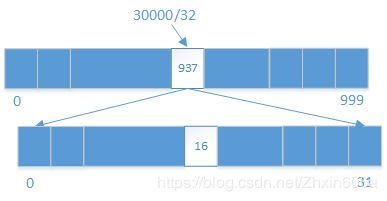
int[] arr=new int[1000];
//一个整型是4个字节，32个比特，则int[] arr=new int[1000];一句申请了32000个比特位
		
int index=30000;
		
int intIndex=index/32;//由除数定位到给定的数在哪个桶中（一个桶32bit）
int bitIndex=intIndex%32;//由余数定位到给定的数在桶中的具体哪个比特位上

arr[intIndex]=arr[intIndex]|(1<

1左移16位=num——>只有第16位上为1，其余为0；

arr[937]和num进行或运算，则num的第16位就置为1了——表示30000这个值在集合中存在了。

怎么得到比特数组？

用基础类型拼，类似于前面的int[1000]——32000个比特位;

若给定的index太大，可换为long[1000]——64000个比特位；

若还是很大，可换为long[1000][1000]——1000*1000*64个比特位。

4.2 上面黑名单的实现

4.2.1 分析

一个url进入布隆过滤器的过程：

• 先使用哈希函数h将url变为一个hashcode，
• 然后hashcode%m得到一个范围在0~m-1的值；
• 将得到的值对应于数组的位置上的值置为1.
• 布隆过滤器是使用k个哈希函数h1~hk，计算k个hashcode，将得到的k个位置上的值置为1.

查一个url是否在黑名单中：

• 将这个url进入k个哈希函数的运算，得到k个值；
• 在给定的数组中查看这k个值对应的位置是否都为1；
  • 若都为1，返回true；
  • 否则返回false。

数组范围应长一点，要不100亿个url进去之后，几乎所有的位置都已置为1了，无法查询——所有的url查询都会返回true。

• 空间越大，失误率越低；
• 空间越小，失误率越高。

哈希函数的个数k，只和url个数有关系，和url具体大小，多少字节无关。

比特数组大小m的计算公式：

• n：样本量——100亿；
• p：预期失误率——万分之一0.0001
• m：单位是bit，算出来小数的话，向上取整。

k也是向上取整

当k和m向上取整之后，真实的错误率为：

【当给定题目后，首先给出经典解法，——占用空间太大——允不允许失误率？——允许——讲解布隆过滤器、算出m（在给定范围内尽量大）,K，再算出真正的失误率，比给定的失误率要低——】

若在乎I/O，则将m内存分布式存储；

5.一致性哈希

5.1 经典服务器抗压结构

当需要加减机器的时候，这个结构就不合适了。所有已存储的数据归属全变了。

——引入了一致性哈希结构

5.2 一致性哈希

可降低数据迁移的代价，同时又负载均衡。

将哈希函数的返回值（）想象为一个环：

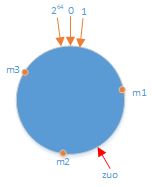
有3台机器m1、m2、m3，假设它们是以IP进行区分的。

• 将m1、m2、m3的IP串经过哈希运算，对应到环上一点。

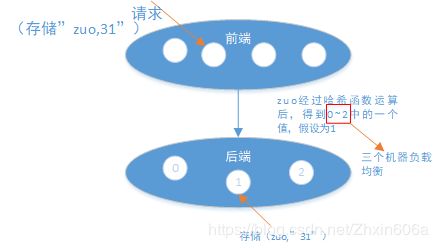
假设存储(zuo,31)，将zuo 进行哈希运算后，不用进行模运算，直接对应到环上一点：

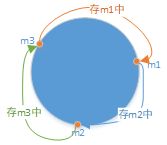
顺时针找到离zuo在环上这一点最近的机器（m2），将（zuo,31）存储在此机器上。

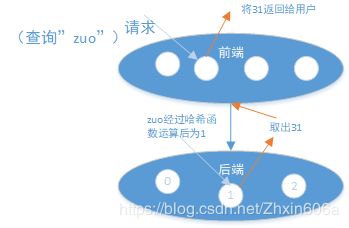
查的时候也一样。

5.2.1 实现

后端还是三台机器，前端还是无差别的负载服务器。

将m1、m2、m3的哈希值排序（有小到大）后组成一个数组{m1,m2,m3}，将这个数组存到前端的每一个服务器中。

当zuo进来后，以二分查找的方式确定它在那个机器上：

• 知道第一个大于等于zuo的哈希值的机器哈希值（以顺时针选的机器）。

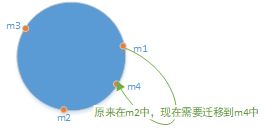
现在需要添加一个机器m4，将它的IP经过哈希运算映射到如图所示的点中：

则需要做数据迁移的部分如图所示：

哈希函数的性质保证的是：量多的情况下，机器数据量均分。

这种结构存在的问题是，机器负载会不均衡。

虚拟节点技术可以解决这个问题。

5.3 虚拟节点技术

有三台机器：m1、m2、m3

给每个节点分配1000个虚拟节点：

• m1：m1-1，m1-2，m1-3，...
• m2：...
• m3：...

准备一个物理映射表：

• 可以从表中得知一个机器有哪些节点；
• 也可知道一个节点属于哪个机器。

令这3000个虚拟节点抢环上的位置，由虚拟节点负责的域，实际上是让它属于的实际机器去处理。——这样就使得三台机器负责的区域是差不多的。

加机器m4时，它也拥有1000个虚拟节点，这些虚拟节点进环，瓜分之前节点的负责的区域。

淡化物理机器的概念，强调虚拟节点的概念。

5.5 应用场景

用到集群特性，抗压的